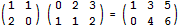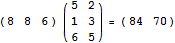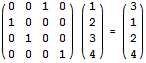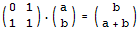预处理指令
    以一个井号开头的行都叫做预处理指令。除了#include指令外，我们还经常用到#define指令。#define指令可以告诉编译器，编译时把代码中出现的特定标识当作什么来处理。例如，我们可以这样写：
#define NAME_OF_MY_POTENTIAL_GF "ZPR"
    这样，编译器会在编译前把代码中出现NAME_OF_MY_POTENTIAL_GF的地方全部替换成"ZPR"。这种替换是无条件的，但是有一个例外：当指定的标识属于某个字符串（被引号引起来）时替换不会发生。例如，下面两行代码会输出NAME_OF_MY_POTENTIAL_GF defined as: ZPR
printf("NAME_OF_MY_POTENTIAL_GF defined as: ");
printf(NAME_OF_MY_POTENTIAL_GF);
    其中，后面那个NAME_OF_MY_POTENTIAL_GF被自动替换为"ZPR"。如果哪一天ZPR不要我了，我就可以非常方便地让整个程序适用于另一个MM。

    C语言中通常会用#define代替const。例如，下面的代码假设了输入数据n<=2000。
#include <stdio.h>
#define MAX 2000

int main()
{
   int f[MAX][MAX];
   int i,j,n;
   scanf("%d",&n);
   for ( i=0; i<n; i++ )
   {
      for ( j=0; j<=i; j++ )
      {
          f[i][j] = j ? (f[i-1][j] + f[i-1][j-1]) % 10000 : 1;
          printf( "%5d" , f[i][j] );
      }
      printf("n");
   }

   return 0;
}

    下面的这些指令也是合法的：
#define begin {
#define end }
#define and &&
#define or ||
    #define定义的指令允许带参数。例如，下面的定义也是合法的：
#define sqr(x) x*x
    观察下面的这个程序：
#include <stdio.h>
#define begin {
#define end }
#define writeln(num) printf("%dn",num)
#define sqr(x) x*x

int main()
begin
   writeln(sqr(100));
   writeln(sqr(10+2));
end
    程序输出：
10000
32
    为什么第二个输出的数是32不是144？不要忘了sqr中的x不是一个变量，编译器仅仅是把x替换为10+2，因此sqr(10+2)的结果是10+2*10+2，当然是32咯。为了避免这种情况，这样写就没问题了：
#define sqr(x) ( (x) * (x) )
    下面这个定义很常用：
#define MAX(a,b) ( ((a) > (b)) ? (a) : (b) )

    如果你想写出一个很有个性的C代码，反复使用#define是一个不错的选择。例如，这段代码就极具个性，一个光棍的形象跃然于屏幕上。然而，真正把#define发挥得淋漓尽致的，还是要数这段代码。

static声明
    在函数中的变量声明前加一个static可以使这个变量具有“记忆性”。观察下面的程序：
#include <stdio.h>
void printNum()
{
   int a=1;
   static int b=1;
   printf("%d %dn", a++, b++);
}
int main()
{
   int i;
   for ( i=1; i<=5; i++ )
       printNum();
   return 0;
}
    程序输出：
1 1
1 2
1 3
1 4
1 5

short类型和int类型的范围
    最初我们列出的C语言类型和Pascal类型的对比只能提供一个参考。事实上不同的编译器中short和int的范围可能不同。你可以查一下前面说过的limits.h来确定这些类型的实际范围。通常short是16位整数，long是32位整数。在Windows下Dev-C++中int类型是32位。

对64位整型的处理
    和Free Pascal一样，对64位整数类型的处理总是比较麻烦。
    首先，对long long赋值很可能会发生错误，你可以在常数后添加一个LL表明这是long long类型。其次，C语言中有些函数是要区分数据类型的，你需要根据数据类型选用恰当的函数。最后，long long类型的输出很可能也有问题，此时你可以用"%lld"来替换"%d"，表明输出的是一个long long类型。在Windows下总要装点怪，我在Windows编译时非要用"%I64d"才行。
    下面的程序代码在Windows下Dev-C++中一切正常。
#include <stdio.h>
#include <stdlib.h>

int main()
{
    long long a;
    a = -5841314520LL;
    a = llabs(a);
    a = a + 1;
    printf("%I64d",a);
    return 0;
}

查漏补缺
    这个系列到这里就结束了。还有我没有说到的语法点吗？欢迎大家补充。

后记
    C语言速成手册到这里就结束了。这很可能是网上现有的原创C语言教材中讲解最快，篇幅最短的，因为它只适合已经学过其它语言，了解程序设计基础知识的人。这一系列的文章略过了大量的概念讲解、示例代码和习题，你可以自己在网上阅读一些C语言程序作为补充。以后我可能还会写一些类似的文章介绍其它语言。下一步我计划写C与C++的区别，对象和类的介绍以及C++的新特性。再以后我可能会向Java或者Ruby的方向发展。
    祝各位努力转C的OIer暑假愉快。

Matrix67原创
转贴请注明出处

条件运算符
    条件运算符的格式如下：
表达式1 ? 表达式2 : 表达式3
    它表示：若表达式1为真（非0），则返回表达式2，否则返回表达式3。

    下面的函数返回两个数中较小的一个：
long min( long a, long b)
{
   return (a<b)?a:b;
}
    很多地方都可能用到条件运算符。再比如求平均数时你可能会这样写：
average = (n>0) ? sum/n : 0;

自加、自减
    a=a+1可以写成a++或++a，a=a-1可以写成a–或–a 。例如，你会经常看到这样的写法：
for ( i=1; i<=10; i++ )
{
}
    如果自加自减不是单独成句，而是放在其它语句中的话，那么a++和++a是有区别的。a++表示“用了后再加”，++a表示“加了后再用”。a–和–a的区别同理。下面的代码输出0 1 1 1。
int a=0;
printf("%d ",a++);
printf("%d ",a);

int b=0;
printf("%d ",++b);
printf("%d",b);

其它运算符
    下面所有的a和b均为整型，则：
C语言  |  Pascal语言
——-+————-
a & b  |  a and b
a | b  |  a or b
a ^ b  |  a xor b
a << b |  a shl b
a >> b |  a shr b

  简写 |    含义
——-+————-
a += b |  a = a + b
a -= b |  a = a – b
a *= b |  a = a * b
a /= b |  a = a / b
a %= b |  a = a % b
a &= b |  a = a & b
a |= b |  a = a | b
a ^= b |  a = a ^ b
a <<= b|  a = a << b
a >>= b|  a = a >> b

各种标准输入输出函数
    下列函数都是stdio.h提供的。stdio.h还提供了一个EOF常量（其实就是-1），用来标识输入数据结束。
         函数                |                    用途
—————————–+———————————————————-
int scanf(str,arg1,…,argn) | 按指定格式读入数据，返回成功被赋值的变量个数。如果已无输入或出错则返回EOF
int printf(str,arg1,…,argn)| 按指定格式输出数据，返回成功输出的字符个数。
int getchar()                | 返回标准输入的下一个字符，如果已无输入或出错则返回EOF。
int putchar(c)               | 向屏幕输出一个字符c，同时返回这个字符，如果出错则返回EOF。
char *gets(str)              | 把这一行输入数据存入字符串str并返回该字符串，如果已无输入或出错则返回NULL
int puts(str)                | 输出字符串并自动输出一个换行符，如果出错则返回EOF。

内存输入输出操作
    stdio.h中提供的sscanf和sprintf两个函数可以把一个字符串当作输入输出对象，其用法与scanf和printf差不多，只不过要多一个参数。你需要把目标字符数组作为函数的第一个参数。
    使用sscanf和sprintf可以方便地进行数字和字符串互转，并实现各种字符串操作。看下面的程序代码：
#include <stdio.h>
int main()
{
    char st[80]="5:43:04";
    int h,m,s;
    
    sscanf(st, "%d:%d:%d", &h, &m, &s);
    printf("Hour:%d Minute:%d Second:%dn", h, m, s);
    
    sprintf(st, "My birthday is %d-%d-%d", 1988, 5, 16);
    printf("%s",st);
    
    return 0;
}
    输出为：
Hour:5 Minute:43 Second:4
My birthday is 1988-5-16

文件输入输出操作
    stdio.h还提供了FILE类型，用于定义文件指针。例如，下面的语句定义了两个待操作的文件：
FILE *in, *out;
    打开一个文件使用fopen函数，该函数的参数为两个字符串。前一个参数指定文件名，后一个参数指定打开模式("r"=读, "w"=写, "a"=在已有文件后继续写 )。函数返回一个文件指针作为此文件的标识供以后使用。

    和文件操作相关的函数有：
         函数                      |                    用途
———————————–+———————————————————-
int fscanf(file,str,arg1,…,argn) | 从file指针对应的文件中读入数据，具体行为同scanf
int fprintf(file,str,arg1,…,argn)| 向file指针对应的文件中输出数据，具体行为同printf
int fgetc(file)                    | 从file指针对应的文件中读入数据，具体行为同getchar
int fputc(c,file)                  | 向file指针对应的文件中输出数据，具体行为同putchar
char *fgets(str,n,file)            | 从file指针对应的文件中读入数据到str字符串，读到第n个字符为止
int fputs(str,file)                | 向file指针对应的文件中输出数据，具体行为同puts
int fflush(file)                   | 立即写入文件，同Pascal中的flush
int feof(file)                     | 文件是否结束，同Pascal中的eof
int fclose(file)                   | 关闭文件，同Pascal中的close

    下面的程序是文件操作版A+B问题，你可以看到文件操作具体的实现方法。
#include <stdio.h>
int main()
{
    FILE *in, *out;
    long a, b;
    
    in = fopen("test.in","r");
    fscanf(in, "%d%d", &a, &b);
    fclose(in);
    
    out = fopen("test.out","w");
    fprintf(out, "%d", a+b);
    fclose(out);
    
    return 0;
}

整型上下限
    Pascal可以用maxlongint来表示longint类型的最大值。C语言中也有类似的定义可以直接使用。使用C语言中的相关定义需要在程序代码前加上#include <limits.h>。

   定义    |    表示
———–+—————————–
CHAR_MAX   | char类型大小上限
CHAR_MIN   | char类型大小下限
SHRT_MAX   | short类型的大小上限
SHRT_MIN   | short类型的大小下限
USHRT_MAX  | unsigned short类型的大小上限
INT_MAX    | int类型的大小上限
INT_MIN    | int类型的大小下限
UINT_MAX   | unsigned int类型的大小上限
LONG_MAX   | long类型的大小上限
LONG_MIN   | long类型的大小下限
ULONG_MAX  | unsigned long类型的大小上限
LLONG_MAX  | long long类型的大小上限
LLONG_MIN  | long long类型的大小下限
ULLONG_MAX | unsigned long long类型的大小上限

常用数学函数
    使用下面的函数需要在程序代码前加上#include <math.h>。

   函数             |     用途
——————–+—————–
double sin(x)       |  正弦
double cos(x)       |  余弦
double tan(x)       |  正切
double asin(x)      |  反正弦
double acos(x)      |  反余弦
double atan(x)      |  反正切
double sqrt(x)      |  开平方
double pow(x,y)     |  x的y次方
double exp(x)       |  e的x次方
double exp2(x)      |  2的x次方
double log(x)       |  以e为底的对数
double log2(x)      |  以2为底的对数
double log10(x)     |  以10为底的对数
double fabs(x)      |  x的绝对值
double fmod(x,y)    |  小数版的mod
double floor(x)     |  小于等于x的最大整数
double ceil(x)      |  大于等于x的最小整数
double trunc(x)     |  舍弃小数部分
double round(x)     |  小数部分四舍五入
long lround(x)      |  小数部分四舍五入，返回long
long long llround(x)|  小数部分四舍五入，返回long long

常用字符串函数
    使用以下函数需要在程序代码前加上#include <string.h>。
    参数s1和s2总是两个字符串，参数c总是一个字符。

    函数               |        用途
———————–+—————————–
int strlen(s1)         | 返回s1的长度
char *strcpy(s1,s2)    | 把s2赋值给s1，返回s1
char *strcat(s1,s2)    | 将s2连接到s1后面，返回s1
int strcmp(s1,s2)      | 比较两字符串，s1小则返回负数，相等返回0，s1大返回正数
char *strchr(s1,c)     | 寻找s1第一次出现c的位置，找到则返回指向该位置的指针，没找到则返回NULL
char *strstr(s1,s2)    | 寻找s2第一次出现在s1的位置，找到则返回指向该位置的指针，没找到则返回NULL
char *strpbrk(s1,s2)   | 寻找s2中的任意字符第一次出现在s1的位置，找到则返回指向该位置的指针，没找到则返回NULL

观察下面的程序：
#include <stdio.h>
#include <string.h>
int main()
{
    char st[80]="matrix67";
    strcat(st,".com");
    printf( "%sn", st );
    printf( "%dn", strlen(st) );
    printf( "%dn", strcmp(st,"my blog") );
    printf( "%cn", *strchr(st,'i') );
    printf( "%sn", strpbrk(st,"3.1415927") );
    printf( "%dn", strstr(st,"x6")-st );

    return 0;
}
输出为：
matrix67.com
12
-1
i
7.com
5

内存操作函数
    下面的一些函数主要用于字符串操作，因此属于string.h 。假设m1和m2都是void *类型。

         函数                |            用途
—————————–+———————————–
int memcmp (m1, m2, n)     |  比较m1和m2的头n个字节，相同返回0，m1小返回负数，m2小返回正数
void *memmove (m1, m2, n)    |  把m2的前n个字节复制到m1的位置，相当于Pascal中的move
void *memset (m1, c, n)      |  把m1的前n个字节全部设为c，相当于Pascal中的fillchar

    下面这段代码的结果是把st字符串变成了"Matrix67, I love UUUUUUUUUUUU…"。
char st[80]="Matrix67, I love someone else...";
memset(st+17,'U',12);
    当然memset更常用的是初始化数组。例如动态规划前初始化f数组：
long f[1000][1000];
memset( f, 0, sizeof(f) );

stdlib.h提供的其它函数
    函数                 |                        用途
————————-+————————————————-
int abs(n)               |  取绝对值，适用于int
long labs(n)             |  取绝对值，适用于long
long long llabs(n)       |  取绝对值，适用于long long
double atof(str)         |  把字符串str转化为数字，返回double类型
int atoi(str)       &n
bsp;    |  把字符串str转化为数字，返回int类型
long atol(str)           |  把字符串str转化为数字，返回long类型
long long atoll(str)     |  把字符串str转化为数字，返回long long类型
void exit(n)             |  退出程序，返回的错误代码为n（0=正常），相当于Pascal的halt
int rand()               |  产生一个随机数，范围在stdlib.h中指定（通常最小为0，最大为int的上限）
void srand(n)            |  设置随机数发生器的种子为n
void qsort(arr,n,size,fn)|  快排，四个参数分别为数组，长度，类型大小，比较函数。

    比较函数的格式应该为
int 函数名(const void *参数1, const void *参数2)
    如果参数1小于参数2，则该函数返回负数，等于则返回0，大于则正数。因此，你可以自己给“大小”下定义。
    下面的程序合法地调用了qsort函数。注意随机函数后的取余运算，这是生成某个范围内的随机数的常用手段。
#include <stdlib.h>
int comp(const void *i, const void *j)
{
    return *(long *)i - *(long *)j;
}

int main()
{
    long n=1000, i, a[n];
    for (i=0; i<n; i++) a[i]=rand()%10000;
    qsort(a, n, sizeof(long), comp);
    return 0;
}

利用assert帮助调试
    assert可以在程序不满足某个条件时输出错误信息并立即终止运行，这对调试很有帮助。使用assert语句需要包含头文件assert.h。观察下面的程序代码：
#include <stdio.h>
#include <assert.h>

int main()
{
    int n;
    scanf("%d",&n);
    assert(n!=0);
    printf("%f",1.0/n);
    return 0;
}
    当读入的数是0时，程序执行printf前就会提前终止，并且输出错误信息。这可以保证后面的语句正常执行，避免异常错误。这显然比用if语句排除异常错误更好一些。在每一个潜在的异常错误前加上assert，当程序出错时你可以很快确定是哪里的问题。

Matrix67原创
转贴请注明出处