大学生活混起来很快,不知不觉又是一年过去了。去年5月10日的ACM校内赛给我留下了许多美好的回忆,因此今年我主动去报了名(上次是被人给拖去的)。今年有点装怪,题目数量不变,但时间缩短为4个小时。原计划是从8:00做到12:00,结果可能是因为我们所在的7号机房迟迟没有开门,时间临时改成了8:15到12:15。总的来说,今年的题目比去年要糟糕得多,但也不乏一些精彩的题目。
和去年一样,第一题依旧是所有题目中最科学的一道。题目给定一个不超过2000*2000的网格,你在最左下角的位置(即(0,0)点),你的目的地在(x,y)。要求你的路线不得经过同一个交叉点两次,且不允许左转(题目背景让这个条件顺理成章:街道靠右行,左转不方便),问合法的路线共有多少种。题目难点就是你不一定要走最近的路,完全允许你绕上一大圈;这破坏了有序性,很难构造出递推公式或动态规划模型。稍微画一下图,我们发现了一些显然但很有启发性的规律:每一次右转后,你左手边方向的所有区域都不能再走了,这很可能产生出规模更小的子问题来。另外,所有合法路线必然是有如螺旋线一样的一圈一圈绕着终点走,这种隐藏的有序性也为动态规划提供了可能。但顺着这个思路想下去屡屡碰壁,我猜不少队伍都卡在这儿了吧。
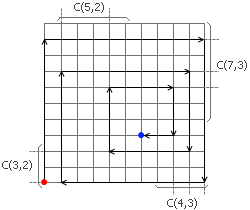
后来我完全打翻前面的全部思路,猛然想到了一个具有决定意义的想法:街道的选取唯一地决定了整个路线。例如,假设我想计算转弯恰好11次的路线有多少条。这样的路线一定含有三条向上走的路、三条向右走的路、三条向下走的路和三条向左走的路。除去第一条路和最后一条路的位置都是确定的,其它的路选在哪一行或者哪一列唯一地决定了整个路线。因此,我们可以用排列组合直接计算出答案来。向上走的路是五选二,向右走的路是七选三,向下走的路是四选三,向左走的路是三选二。把它们各自的选取方案数乘起来就得到了拐弯11次的合法路径。于是,计算所有的路线数只需要从小到大枚举拐弯的次数,每一次计算都是常数的,总复杂度是O(n)的;整个算法的瓶颈反倒是O(n^2)的组合数预处理,不过这个复杂度完全可以承受。

