
逻辑
如果我说的是假话,那么我说的是假话
在准备一份数理逻辑的材料时,我创作了下面 10 个逻辑推理问题。在每个问题中,甲、乙、丙三人各说了一句话,你需要判断出每个人说的究竟是真话还是假话。每个问题都有唯一解。注意,与传统的逻辑推理题目不同,没有任何条件告诉你究竟有多少人在说真话,有多少人在说假话。解决问题时尽量避免用枚举法试遍所有 8 种可能,否则这将失去“逻辑推理”的意义。
(1) 甲:乙说的是假话
乙:丙说的是假话
丙:甲要么说的是真话,要么说的是假话
答案:显然,丙说的是真话。
因此,乙说的是假话。
因此,甲说的是真话。
数学无处不在:语言、文字与数学
(拜托转载时请用红色加粗字体标明,这是我古今数学思想课的期中论文,免得老师以为我是反过来抄的网上的文章。这门通选课的期中论文要求写数学与自己所在专业之间的联系。)
我们每天都在说话,每天都在用语言进行交流。语言文字对我们是如此的平常,以至于绝大多数人都不会注意到语言中一些非常难以解释的现象。昨天的汉语虚词研究课上,我们就谈到了这样一个有趣的问题:在表示“仅仅”的含义时,什么时候能够用“只”,什么时候能够用“光”?若不细想的话,大家或许会认为两者的用法完全一样。“我只吃苹果”可以说成“我光吃苹果”,“光有知识还不行”也可以说成是“只有知识还不行”。我们还可以举出更多的例子来,如“别光坐着”/“别只坐着”,“光说不做”/“只说不做”等等。凭借天生的归纳性思维,一个正常人有充分的理由猜想,在表示“仅仅”的含义时,“只”和“光”是通用的。而事实上,现代汉语词典中正是把“光”字解释为“只”。有趣的是,在我们质疑只找了四个例子是否足以说明二者等价时,殊不知这句质疑本身就成了一个反例:“只找了四个例子”不能换成“光找了四个例子”。类似地,“大会只来了748个人”也不能说“大会光来了748个人”。我们继续猜想,是不是“光”不能用在数量词前面呢?也不见得。当数量词不是实指而是虚指时,我们有时也能用“光”来修饰带有数量词的名词。例如,在表示“只吃几个苹果”、“只吃一些苹果”的意义时,“光吃两个苹果”的说法是很顺口的。另一些例子则表明,“光”的用法似乎与它所修饰的名词无关。“我只当到团长”不能说成是“我光当到团长”,但怪就怪在“我只认识团长”却又偏偏可以说成是“我光认识团长”。“当到团长”和“认识团长”有什么不同呢?仔细揣摩两者的意思,我们似乎体会到了一些微妙的差别:“当到团长”是一个阶段性的、进度性的、里程碑性的概念,它必须事先经过“当到连长”、“当到营长”等事件;但“认识团长”就不一样了,没有任何规定限制我们在“认识团长”之前必须“认识连长”。同样的,“找出四个例子”是以“找了三个例子”为前提的,“来了748个人”也不是一下子就能实现的。
问题算是想通了,但怎么来阐述它呢?在这个问题上,语言学陷入了一个困境。此时,引入数理逻辑语言对于解释这种语言现象出乎意料的方便。我们说,在副词“只”修饰的事件所处的“域”中如果存在蕴含关系,则这里的“只”不能用“光”来替代。例如,提起“吃两个苹果”,我们脑海中形成的事件集合一定是“吃一个苹果”、“吃两个苹果”、“吃三个苹果”等等,而后者必然蕴含前者,因此“只吃两个苹果”不能说成“光吃两个苹果”。类似的,“当到团长”必然推出“当到连长”,但有“认识团长”不见得有“认识连长”,因此两者与“只”和“光”的搭配情况是不同的。
运用条件概率分析合情推理模式
1. Goldbach猜想是说,任一大于等于4的偶数一定能表示成两个质数之和。关于质数,我们还有这样一个有趣的结论:对于任何整数n>1,存在质数p满足n<=p<2n。这个结论对Goldbach猜想是很“有利”的,因为它是Goldbach猜想的一个必要条件。倘若对于某个正整数n,n和2n之间没有质数,那么偶数2n就不能表示为两个质数之和了,因为所有可以用的质数都比n小,再怎么也加不出2n来。注意,如果这个结论错了,猜想也就被推翻了;但如果这个结论对了,猜想也不一定是对的。但即使这样,我们仍然习惯性地认为,验证了推论的正确性后猜想的可靠程度也或多或少的有了些提高,换句话说猜想为真的可能性更大了。这种思维合理吗?
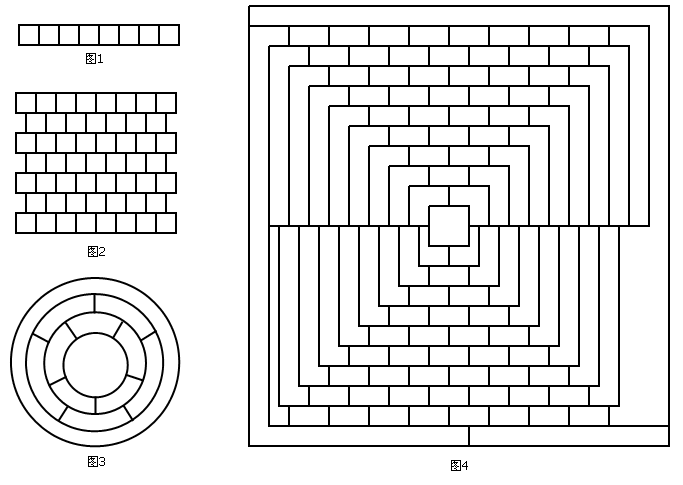
2. 长期以来,人们都在思考:对任一给定的平面图进行染色,要想使得有公共边的区域颜色不同,最少需要多少种颜色。四色猜想(现在已经是四色定理了)认为,只需要最多四种不同的颜色就足够了。我们可以随便画一些图进行验证,每一次检验后我们都会或多或少地更加相信结论的正确性。你可以尝试寻找下面的图1、图2和图3的合法解,检验一下猜想是否正确。验证哪一个图更有价值?你或许会这样回答:验证第一个图毫无价值,因为它显然有可行的染色方案;验证第三个图最有价值,因为它看上去最像反例,证实了它确实有解后,你会更加坚信四色猜想的正确性。1975年的4月1日,杂志Scientific American的数学专栏作家Martin Gardner宣布他找到了一个四色猜想的反例(图4)。当然,这只是一个愚人节的笑话。寻找图4的解非常困难,以致于看上去几乎是不可能的。一旦你成功找出了图4的解,对四色猜想的信任程度可就不只提高一点点了。“对猜想的某个结论进行验证,结论越是不可思议,证实以后原猜想的可靠程度就提高得越多”,这种思维是合理的吗?
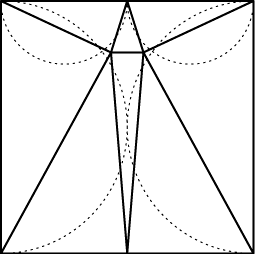
3. 你认为,是否有可能把一个直角三角形分成若干个锐角三角形?你很可能花了一节古代汉语课的时间苦思冥想,结果直角三角形没搞出来,倒是碰巧把一个正方形分成了8个锐角三角形。虽然你仍不知道一个直角三角形是否能分成若干个锐角三角形,但你找到了一个正方形的解,你会强烈地感觉到直角三角形也是有解的。这是什么原因呢?注意到,如果三角形能分的话正方形一定能分,但反过来却不一定。不过,这里面还有一些更微妙的关系:我们倾向于相信如果连直角三角形都没法分,正方形应该更没法分了。既然现在正方形已经解决了,那三角形也就快了。“B是A的结论,且没有A的B很不可靠,则证实了B可以极大地提高A的可信度”,这种思维合理吗?
4. 关于“如果他错了,那我对的概率就更大了”的思维。A、B两人被一个实际问题难住了,双方就问题中的两个变量的变化关系争执不休。A认为,函数图像画出来应该是一个开口朝上的二次函数;B则认为,函数图像应该是一个正弦函数。注意到一个有趣的事实:这两种猜测满足矛盾率,但不满足排中率。就是说,有可能A和B都错了,但是A和B不可能都对。紧接着他们发现,这个函数存在至少一个极大值,A的猜测显然是错的。虽然这并不能表明B的猜测就是对的,但我们能不能说B猜对的概率变大了?
下面的内容是G.Pólya的Mathematics and Plausible Reasoning Vol 2里的精华:用概率来分析合情推理模式。我们可以用概率知识来描述上面这些合乎情理的推测。如果你还不知道什么叫做条件概率,建议你先看一看这篇文章。
注意到P(A)*P(B|A)永远等于P(B)*P(A|B),它们都等于P(A∩B)。如果B是A的一个推论,那么有P(B|A)=1(若A为真则B必为真)。于是我们有P(A)=P(B)*P(A|B)。这里,P(A|B)有一个形象的意义:结论B的证实可以使我们对A的信任改变多少。假如P(A|B)不变,则如果等式右边的P(B)增加了,P(A)也会增加。这也就说明了我们的第一个合情推理模式:对猜想的一个结论更加信任,对猜想本身也更加信任。
这个式子还能告诉我们更多的东西。把P(B)除过去,我们有P(A|B)=P(A)/P(B),其中等式左边的P(A|B)表示的仍然是证实了B以后A为真的概率,也就是验证B结论的价值。我们很清楚地看到,P(B)处于分母的位置。那么,结论B本身为真的概率越小,证实了B后对A的影响也就越大。
注意P(B)=P(A∩B)+P(~A∩B)=P(A)*P(B|A)+P(~A)*P(B|~A),而B是A的一个结论,即P(B|A)=1。于是,等号右边变为P(A)+[1-P(A)]*P(B|~A)。利用前面的结论,我们用P(A)/P(A|B)代替等式左边的P(B),则有P(A|B)=P(A)/[P(A)+[1-P(A)]*P(B|~A)]。可以看到,如果P(B|~A)越小,则P(A|B)越大。这就是说,在没有A的前提下B成立可能性越小,证实了B之后A为真的可能性就越大。
最后,我们看一看A和B不相容的情况。此时,P(A∩B)=0,于是
P(A) = P(A∩B) + P(A∩~B)
= P(A∩~B)
= P(~B) * P(A|~B)
= [1-P(B)] * P(A|~B)
把1-P(B)除过去,就有P(A|~B)=P(A)/[1-P(B)],显然P(A|~B)是大于P(A)的,也即排除了B的猜测后A对的可能性比原来更高了。我们还可以清楚地看到,如果我们之前越相信B,则B被驳倒后A正确的可能性提高得就越多。
100囚犯问题、100囚犯问题加强版与选择公理(下)
无穷个囚犯面向数轴的正方向依次就座,第i个囚犯坐在数轴上坐标为i的地方,他可以看见所有坐标大于i的囚犯头顶上的帽子。看守给每个囚犯戴上黑色或白色的帽子,然后依次叫每个囚犯猜测自己头上的帽子颜色,猜对了的予以释放。另外一点和原来不同的是,囚犯们不能听到其他人的猜测。另外注意到,由于每个人前面都有无穷多个人,因此囚犯们无法通过数他前面的人数来判断出自己的位置,于是我们不得不加上一句:每个人都知道他后面有多少人(即他是第几个被问的)。同样地,事先所有囚犯可以商量出一个策略。你认为这下囚犯们还有什么好办法没?
这下囚犯已经不能通过自己的猜测来通风报信了,似乎每个人都只能瞎猜,任何人都无法保证自己能猜对。你相信吗,居然有这样的策略,它可以保证除了有限个囚犯之外,其他囚犯全部释放!
考虑所有可能的颜色序列(你可以简单地想像成01串)。我们说两个颜色序列“无穷远相等”,如果经过了有限多项之后,余下的无穷多项完全相同(即存在某个数x,使得两个串在各自的第x位后面完全重合)。这种关系显然满足自反性、对称性和传递性,是一种等价关系。因此,按照这种有限位后对应相等的关系,我们可以把所有可能的颜色序列划分为一个个等价类。它们的交集为空(两个等价类如果有交集,由传递性它们立即并成了一个更大的等价类),并集为全集(若某序列不属于任何等价类,则它自己就是一个新的等价类),是全集的一个划分。你能想象出一个等价类大致是什么样子的吗?假如把同一个等价类里的所有序列对齐并排放在一起,你从前往后走过去的时候会发现这些序列“越来越相像”。你走得越远,你会发现越来越多的序列开始变得互相重合;当你走到无穷远时,所有的序列都变成一个样了。
囚犯们事先在每一个等价类中选一个代表元,然后把所有等价类的代表元背下来。到时候,每个人都能够看到他前面无穷多个人的帽子颜色,并且知道他自己在整个序列的位置,于是能立即判断出他们现在所处的颜色序列在哪个等价类里。接下来,他们只需要按照事先背好的代表元来猜就行了。由“无穷远相等”的定义,经过有限次猜测后最终这个代表元会和他们所处的序列重合,于是除了前面有限多个人以外,以后无穷多个人都可以保证猜对。
你是否觉得这种“策略”很不合理,虽然从逻辑上看每一步推理都是无懈可击的?有人认为,这是选择公理带来的悖论。选择公理是说,给你一系列的集合(可能有无穷多个),那么我们总可以在每一个集合里取出一个元素来。这并不是显然正确的。你不可以依次考虑每个集合,从里面随便取出一个元素来,因为集合个数有可能无穷多个(甚至不可数),这样的操作将永无止境,不允许出现在数学推理过程中。我们需要定义一套系统,使得它对于给定的每一个集合都适用,这样我们就可以“一下子”处理完所有的集合。换句话说,对于一组数量任意多的集合,我们需要定义一个函数f,使得对其中任一集合S,f(S)为S里的一个元素。我们称函数f为选择函数。例如,给出自然数集的所有子集,选择函数f可以定义为“集合中的最小元素”;给出实数集的所有有限长的区间,则选择函数f可以定义为“区间的中点”。但对于某些情况,目前还没有办法用之前已有的公理系统定义出合适的选择函数。比如,目前仍然不清楚,对于实数集的所有非空子集是否存在一个选择函数。但选择函数的存在是很多数学推理的前提假设。因此,我们有必要承认选择公理,构成新的公理体系(即ZFC公理体系)。于是在今后的数学推理中,我们可以假设存在这样一个超级选择函数f,它就是专门用来干这破事的。承认选择公理有可能推出一些与生活经验背道而驰的结论,最著名的就是Banach-Tarski悖论:你可以把一个三维球体分成有限多块,然后拼接组合成两个和原来一样大的球体。上面所提到的100囚犯问题加强版则是选择公理带来的另一个悖论。
参考资料:http://cornellmath.wordpress.com/2007/09/13/the-axiom-of-choice-is-wrong (墙就是强)