今年一月份，California的一个数学艺术展览会上出现了这样一种神奇的三维图形。放出图片之前，你能根据下面的文字描述想象出这个图形的样子吗？
给定一个单位大小的立方体，在其中5个面的中心放置一个边长为1/2的小立方体；这5个小立方体中的每一个都有5个面露在外面，在这25个面中的每一个面中心再向外拼接一个边长为1/4的小立方体；然后每个1/4小立方体的5个暴露在外的面上再放置1/8大小的立方体……不断迭代下去后，最终会形成一个什么样的三维图形？
上图就是按照要求迭代11次的样子，里面那个斜着放的红色立方体是最初的那个单位立方体，外面拼接了5个橙色立方体，每个橙色立方体外面又拼接了5个黄绿黄绿的小立方体……最终的形状大致是一个四棱锥，上面有很多三角形的洞，这些被挖去的部分恰好组成了最经典的分形图形——Sierpinski三角形。这是由艺术家Robert Fathauer发现的，在展览上的名字叫做Fractal Crystal No.1。
查看更多：http://www.bridgesmathart.org/art-exhibits/jmm08/
Menger海绵(Menger Sponge)是三维空间中的经典分形图形，是Sierpinski地毯的三维扩展，最先由数学家Karl Menger提出。它的构造完全仿照Sierpinski地毯的构造方法，只是把平面上的地毯改成了空间中的海绵：把立方体分成27个小立方体，挖掉每一面中心和整个立方体中心共7个小立方体，对剩下的20个立方体递归地进行操作。它的Hausdorff维度为(ln20)/(ln3)，约等于2.726833。你能想象出它的截面是什么样子的吗？偶然发现这样一个奇图，发上来与大家分享：
图片来源：http://flickr.com/photos/sbprzd/1432723128/
SETI@home可以在杂乱的射电数据中搜寻独特的讯号，你能在大街上的嘈杂声中清晰分辨出一个尖细的女声大叫“亚美蝶”。这些现象都表明，有时对集合里的所有元素进行整体考察可以很快找出我们所要找的个体。去年我们搞合唱比赛时，我又想到了一个绝佳的例子：你可以在合唱声中清楚地听到是否有人跑调。考虑这样一个问题，假如合唱团里有一个人唱歌始终走调，但我听不出来是谁走调，只能听出当前正在唱歌的人中是否有唱走调了的人。那么，我如何才能迅速地揪出那个唱走调的人？利用经典二分法，我们可以在log2(n)次合唱后找出唱走调了的人。每一次，我都把剩下的人平均分成两组，然后选其中一组来合唱：如果听不到走调的声音，这一组的人就全部过关；如果听到有人走调，那另一组里的人都可以被排除了。递归地对剩下的组进行同样的操作，log2(n)次操作后必定可以找出那个唱歌走调的人。
现在的问题变得有些麻烦了。假如我们知道合唱队里有一个人唱歌爱跑调，但他不是总会跑调。具体地说，他只有1/2的概率唱错，但其余1/2的时间里他却唱得很准。现在，传统的二分法不再适用了，因为没有走调声已经不能起到排除的作用了。你能想出多少种可行的算法来找出那个人？下面提出一些可行的方法，你认为哪种方法更好？你能求出这些算法所需要的检测次数的期望值各是多少吗？
1. 不断地随机生成一个大小为n/2的子集并对其进行检测，直到某次不能通过检测为止，然后递归地对其进行操作。
2. 所选的子集大小为n/2是最优的吗？把上面这种方法的n/2改成n/a，常数a的最优值是多少？
3. 检测次数的期望值还可以更小吗？我们想到，每次都重新生成一个新的集合其实并不科学，新集合本身是否包含老鼠屎也是得碰碰运气的。因此，对方法1的一个合理改进是：把集合平均划分为两个部分，交替对它们进行检测直到某次检测没通过为止，然后对该组递归操作下去。这种方法真的比前两种好吗？它所需要的期望次数是多少？
4. 尝试对方法3进行改进。如果把集合平均划分成3份并循环进行检测，效果会不会更好一些？
1. 选取的子集有1/2的概率覆盖了我们要找的那个人，子集里有他而他这次恰好又唱走调了则有1/4的概率。因此，不管规模有多大，平均需要4次才能把规模缩小一半。因此，检测次数的期望值为4*log2(n)。为了方便比较期望值的大小，后面的答案我们一律表示成一个常数乘以log2(n)的形式。
2. 类似地，平均需要2a次检测才能把规模缩小到原来的1/a，因此总共花费的检测次数为2a*log2(n)/log2(a)。对函数求导，可得当a为e时函数值达到最小。此时的检测次数期望值为2e*log2(n)/log2(e)≈3.7683 * log2(n)。
3. 这个就经典了。设方法3里把规模缩小一半所需要的检测的期望次数为m，下面我们来看m应该等于多少。把n个人平均分成两组，我们要找的老鼠屎有1/2的概率在第一组，有1/2的概率在第二组。因此，第一次就测出问题来有1/4的可能，第二次就测出问题也有1/4的可能。对于剩下的1/2种情况，局面变得又和最开始一样，只是平均需要的检测次数比原来多了2。根据期望值的定义，有m=(1/4)*1 + (1/4)*2 + (1/2)*(m+2)，解得m=3.5。总的检测次数就是3.5 * log2(n)，它比前面两种方法都要好。你可能不同意上面求m的方法。这没啥，如果你不断对m进行迭代，你会发现展开出来的式子就是最标准的期望值定义。
4. 类似地，有m=(1/6)*1 + (1/6)*2 + (1/6)*3 + (1/2)*(m+3)，解得m=5。于是，把规模缩小到原来的1/3平均需要5次检测，总的检测次数为5*log2(n)/log2(3)≈3.1546 * log2(n)。
题目来源：IBM Ponder This Dec07
原文还从熵的角度探寻了问题的最优算法，感兴趣的读者可以去看一看
从2007年分形艺术大赛(Benoit Mandelbrot Fractal Art Contest)中选了几个自己感觉不错的图与大家分享。
图片按以下三个原则来选取：
1. 严格符合分形图形的定义
2. 与以往的分形图形风格很不一样
3. 很好看:)
查看全部获奖作品：http://www.fractalartcontests.com/2007/winners.php
查看全部参赛作品：http://www.fractalartcontests.com/2007/entries.php
一个正整数n的阶乘就是前n个正整数的乘积，我们通常需要n-1次乘法操作来算出精确的值。不像等差数列求和、a的n次幂之类的东西，目前求阶乘还没有什么巨牛无比的高效算法，我们所能做的仅仅是做一些小的优化。
更少的乘法运算次数？
在高精度运算中，乘法计算的速度远远慢于加减法，因此我们有必要减少乘法运算的次数。下面我将做一个非常简单的变换，使得计算阶乘只需要n/2次乘法。继续看下去之前，你能自己想到这个算法来吗？
我们可以把一个数的阶乘转换为若干个平方差的积。例如，假如我想求9!，我可以把前9个正整数的乘积写成这个样子：
1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9
= (5-4) * (5-3) * (5-2) * (5-1) * 5 * (5+1) * (5+2) * (5+3) * (5+4)
= (5-1) * (5+1) * (5-2) * (5+2) * (5-3) * (5+3) * (5-4) * (5+4) * 5
= (5^2 – 1^2) * (5^2 – 2^2) * (5^2 – 3^2) * (5^2 – 4^2) * 5
注意到一个有趣的事实：上面的四个平方差算出来分别是24, 21, 16, 9，它们之间的差正好是连续的奇数（因为n^2等于前n个正奇数的和）。因此，我们可以用初始数(n/2)^2不断减去一个个的正奇数，求出所有n/2个平方差，再用n/2次乘法把它们乘起来。这种算法实现起来非常简单，并且（当n不大时）同样只需要单精度乘高精度，但需要的乘法次数大大减少了。假设我们已经有了一个高精度类，求n!只需要下面几句话：long h=n/2, q=h*h;
long r = (n&1)==1 ? 2*q*n : 2*q;
f = LargeInteger.create(r);
for(int d=1; d<n-2; d+=2)
f = f.multiply(q-=d);
更少的总运算次数？
尽量提取阶乘中的因子2，我们可以得到另一种阶乘运算的优化方法。这很可能是不需要分解质因数的阶乘算法中最快的一种。
假如我们需要计算20!，我们可以把20拆成若干组正奇数的乘积：
1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 * 10 * 11 * 12 * 13 * 14 * 15 * 16 * 17 * 18 * 19 * 20
= 1 * 3 * 5 * 7 * 9 * 11 * 13 * 15 * 17 * 19 * 2 * 4 * 6 * 8 * 10 * 12 * 14 * 16 * 18 * 20
= 1 * 3 * 5 * 7 * 9 * 11 * 13 * 15 * 17 * 19 * 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 * 10 * 2^10
= 1 * 3 * 5 * 7 * 9 * 11 * 13 * 15 * 17 * 19 * 1 * 3 * 5 * 7 * 9 * 2 * 4 * 6 * 8 * 10 * 2^10
= 1 * 3 * 5 * 7 * 9 * 11 * 13 * 15 * 17 * 19 * 1 * 3 * 5 * 7 * 9 * 1 * 2 * 3 * 4 * 5 * 2^15
= 1 * 3 * 5 * 7 * 9 * 11 * 13 * 15 * 17 * 19 * 1 * 3 * 5 * 7 * 9 * 1 * 3 * 5 * 2 * 4 * 2^15
= 1 * 3 * 5 * 7 * 9 * 11 * 13 * 15 * 17 * 19 * 1 * 3 * 5 * 7 * 9 * 1 * 3 * 5 * 1 * 2 * 2^17
= 1 * 3 * 5 * 7 * 9 * 11 * 13 * 15 * 17 * 19 * 1 * 3 * 5 * 7 * 9 * 1 * 3 * 5 * 1 * 2^18
只需要一次累乘就可以求到每一组奇数的乘积，最后再花费log(n)次乘法把它们全部乘起来。最后的那个2^18也可以二分计算出来。真正的代码还有很多细节上的优化，另外还借用了递归使得操作变得更加简便。你可以在本文最后附的那个链接里去找Split-Recursive算法。
还能再快一点么？
继续扩展上面的算法，我们可以想到，如果把每个数的质因数都分解出来，并且统计每种质因子有多少个，我们就可以多次使用二分求幂，再把它们的结果乘起来。注意这里并不是真的要老老实实地去分解每个数的质因子。对于每个质数x，我们可以很快算出前n个正整数一共包含有多少个质因子x（记得如何求n!末尾有多少个0么）。这种算法的效率相当高，已经能够满足大多数人的需要了。
另一种诡异的阶乘算法：
这个算法可能是所有有名字的阶乘算法中最慢的一个了（Additive Moessner算法），它对一个数列进行重复的累加操作，一次次地计算前缀和，总共将花费O(n^3)次加法操作。但是，令人费解的是，这个简单的程序为什么可以输出前n个正整数的阶乘呢？a[0]:=1;
for i:=1 to n do
begin
a[i]:=0;
for j:=n downto 1 do
begin
for k:=1 to j do
a[k]:=a[k]+a[k-1]
write(a[i],' ');
end;
end;
我在网上搜索相关的东西时找到了另一个有趣的东西。对一个初始时全为1的数列反复进行这两个操作：累加求前缀和，然后以1,2,3,…的间隔划掉其中一部分数（即划去所有位置编号为三角形数的数）形成新的序列。类似的数列操作方法最先由Alfred Moessner提出的，我们这里不妨把它叫做Moessner数列。你会发现，第n轮操作开始前，数列的第一个数恰好是n! 。看看下面的例子吧：
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 …
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 …
x 2 x 4 5 x 7 8 9 x 11 12 13 14 x …
2 4 5 7 8 9 11 12 13 14 …
2 6 11 18 26 35 46 58 71 85 …
x 6 x 18 26 x 46 58 71 x …
6 18 26 46 58 71 …
6 24 50 96 154 225 …
x 24 x 96 154 x …
24 96 154 …
24 120 274 …
x 120 x …
120 …
…..
当然，发现前面O(n^3)的程序和这个Moessner数列的关联时我很是吃了一惊：在前面的程序里，如果你输出每一次i循环末所得到的数列，你会发现输出的这些数正好就是后面这个问题里被我们划掉的数，而它们其实就是第一类Stirling数！
这到底是为什么呢？是什么东西把阶乘、第一类Stirling数、Moessner数列和那个O(n^3)的程序联系在一起的呢？昨天，我想这个问题想了一天，最后终于想通了。如果把Moessner数列排列成这个样子，一切就恍然大悟了：
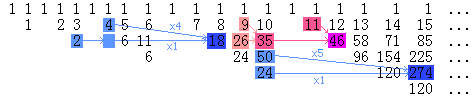
仔细观察上图，我们会发现：
1. 按照Moessner数列的定义，每个数都应该等于它左边的数和左上角的数的和（这个“左边”可以跳过若干空格）。例如，35 = 9 + 26，46 = 11 + 35。排成一系列三角形后，每个三角形最右边一列的数就是被划去的数，它永远不能参与它下面的那些行的运算。
2. 设a[n,i,j]表示左起第n个三角形阵列中的第i行右起第j列上的数，则a[n,i,j]=a[n-1,i-1,j]*n + a[n-1,i,j]，例如274=50*5+24。如果递推时遇到空白位置而它左边隔若干空格的地方还有数的话，则需要用左边的数来补，例如18=4*4+2。对于每个三角形的最后一列来说，这个性质实际上就是第一类Stirling数的递推关系，因此Moessner数列中才会出现第一类Stirling数。
3. 在第一类Stirling数中，s(n,1)=n! ，也即左起第n个三角形最底端的那个数等于n!。从上面的第二个性质来看，这也是显然的。
4. O(n^3)的算法实际上就是在绘制上面这个图。每一次j循环末，我们得到
的序列是第i个三角形中每一行左起第j个数组成的序列。例如，计算第5个三角形内的数时，程序首先累加出1, 11, 46, 96, 120, 120，这样便算出了a[5]=120，数列的前5个数再次累加即得到1, 12, 58, 154, 274，由此算出a[4]=274。
第二个性质可以利用第一个性质进行数学归纳法证明，证明很简单，我就不多说了。现在我尽可能少写一些繁琐的细节，节约一些时间用来复习古代汉语。
做人要厚道，
转贴请注明出处。
查看更多：
http://www.luschny.de/math/factorial/FastFactorialFunctions.htm
http://www.luschny.de/math/factorial/index.html <—- 巨牛，20多种阶乘算法的代码！