图片来源：http://xkcd.com/688/
真是太有才了！
递归
瓶魔悖论与不完全信息
The Bottle Imp 是一则有意思的短篇小说。某日，小说里的主人公遇上了一个怪老头。怪老头拿出一个瓶子，说你可以买走这个瓶子，瓶子里的妖怪就能满足你的各种愿望；但同时，持有这个瓶子会让你死后入地狱永受炼狱之苦，唯一的解法就是把这个瓶子以一个更低的价格卖给别人。如果你是小说里的主人公，你会不会买下这个瓶子呢？你会以什么价格买下这个瓶子呢？
以什么价格买入这个瓶子，这个问题貌似并不容易回答。你当然不愿意花太多的钱，在你的愿望被满足之前你至少还得给自己留一点钱花；但你也不能花太少的钱，否则你会承担着卖不出去的风险。但是，在做出一些理性的分析后，我们得出了一个惊人的结论：任何人都不应该以任何价格购买这个瓶子。
和很多博弈问题一样，这一系列的分析首先从最简单的情形开始。首先，你是绝对不能只出 1 分钱就买下这个瓶子的，因为这样的话这个瓶子就永远也卖不出去了——没有比 1 分钱更低的金额了。那么，用 2 分钱买瓶子呢？这样理论上貌似是可行的，但仔细一推敲你会发现还是有问题——这样你只能以 1 分钱卖掉这个瓶子，但没有人会愿意用 1 分钱去买瓶子（否则他就卖不掉了）。因此，用 2 分钱买下瓶子后，你同样找不到下一个买家。和上面的推理一样，用 3 分钱买这个瓶子也不是什么好主意，因为没有人愿意以 1 分钱或 2 分钱购入瓶子，因此你的瓶子不可能卖得掉。依此类推，你不应该以任何价钱去购买这个瓶子，因为每个人都知道，他无法以任何价格卖掉这个瓶子。
地球上惊现Sierpinski贝壳？
我一直在思考，利用物理性质和数学算法之间的一些联系，能否设计出某种物理系统可以直接产生出诸如Sierpinski三角形甚至Mandelbrot集一类的分形图形。事实证明，大自然的力量是无穷的。reddit上的一位网友发现一个上面长着Sierpinski三角形模样的贝壳。这到底是为什么呢？难道有什么自然规律正好与Sierpinski三角形的某种生成方法相吻合？
经典证明：推箱子游戏所需步数可达指数级
今天在写一个稿件时又翻阅了一下Erich Friedman的Math Magic，发现了一个有趣的东西——场地大小为n的推箱子游戏所需要的最少步数最坏情况是多少。下面这个构造说明，最坏情况至少也是指数级的。
首先，让我们来看看该构造中的一个基本单元：
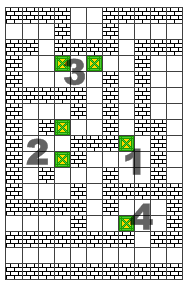
这个构造中共有6个箱子，且它们都已经在目的位置上了。不难看出：
1. 假如你人在这个区域之外，你只可能从右上角的出入口进入该区域，从其它地方进去都会导致死局
2. 从右上角进入后你只能往下走，进入1区；走左边的话直接导致死局
3. 你可以通过2区前往3区，但若从3区左上角的出口出去了，则2区动过的箱子将永远无法回到原位（除非你原路返回）
4. 你可以通过2区前往3区，并把3区左边的那个箱子左移一格，再返回2区；这样下次你再从右上角进入该区域时便可以直接经过3区从左上角出去
5. 最后你只能从4区离开
