用摄像机对准三个屏幕，每个屏幕都显示摄像机拍到的内容，于是整个图形就是由三个与整体自相似的图形构成的，分形便诞生了。
这毫无疑问是我见过的最简单、最聪明、最酷的分形图形制作方法！
来源：http://scientopia.org/blogs/goodmath/2010/11/02/fractals-without-a-computer/
递归
There is always a bigger fish
Always A Bigger Fish 不但是电影情节中的经典桥段，也是各种恶搞的灵感来源——小鱼总是被大鱼吃掉，而大鱼上面总还有更大的鱼。久而久之，聪明的大鱼或许就不会去吃小鱼了，否则按照传统剧情，它身后会出现一条更大的鱼。一个有趣的问题出现了：倘若所有的鱼都是理性的，那会出现怎样的情况呢？
让我们把问题重新叙述一下。假设有 n 条鱼，它们从小到大依次编号为 1, 2, …, n 。我们规定，吃鱼必须要严格按顺序执行。也就是说，大鱼只能吃比自己小一级的鱼，不能越级吃更小的鱼；并且只有等到第 i 条鱼吃了第 i – 1 条鱼后，第 i + 1 条鱼才能吃第 i 条鱼。第 1 条鱼则啥都不能吃，只有被吃的份儿。我们假设，如果有小鱼吃的话，大鱼肯定不会放过；但是，保全性命的优先级显然更高，在吃小鱼之前，大鱼得先保证自己不会被吃掉才行。假设每条鱼都是无限聪明的（并且它们也都知道这一点，并且它们也都知道它们知道这一点⋯⋯），那么第 1 条鱼能存活下来吗？
比乘法更大的是乘方，比乘方更大的是什么？
小学时，老师说，由于生活中经常需要把同一个数加很多很多次，因此人们发明了乘法。 a × b 就表示 b 个 a 相加。初中时，老师说，由于生活中经常需要把同一个数乘很多很多次，因此人们发明了乘方。 a ^ b 就表示 b 个 a 相乘。令人失望的是，到了高中时，我们并没有学到更牛 B 的运算符号；大学都快学完了，似乎也没见到乘方升级的苗头。乘方之上究竟是什么？下面，有请今天的主角——超级幂——登场！
很容易想到，比乘方更大一级的运算就是把 b 个 “a 次方” 重叠起来。不过，这里我们却遇到了一个之前不曾遇到的问题： a ^ a ^ a 究竟应该等于 (a ^ a) ^ a ，还是 a ^ (a ^ a) ？。我们不妨来算一算，不同算法得到的结果相差多远：
(2 ^ 2) ^ 2 = 4 ^ 2 = 16
2 ^ (2 ^ 2) = 2 ^ 4 = 16
难道两种不同的计算顺序，得到的结果总是相同的吗？让我们换 a = 3 试试：
(3 ^ 3) ^ 3 = 27 ^ 3 = 19683
3 ^ (3 ^ 3) = 3 ^ 27 = 7625597484987
哇，这下可就差远了。可以想象，如果把 “a 次方” 再多迭代几次，从右往左算和从左往右算会差得更多。恐怖的是，当有多重指数时，运算正是按照从右往左算的顺序进行的。试想，若有一种运算专门用来表示 b 个 a 构成的指数塔，这种运算的威力会多大。
中文自我描述句
我曾经在这里介绍过一种叫做 autogram 的文字游戏，简单说就是“与自身相符的句子”，或者更简单地叫做“自我描述句”。例如，“这句话是用中文写的”、“这句话有七个字”等等。蛋疼的人还真不少，有人创作出了一些异常牛 B 的 autogram ，比如：
This autogram contains five a’s, one b, two c’s, two d’s, thirty-one e’s, five f’s, five g’s, eight h’s, twelve i’s, one j, one k, two l’s, two m’s, eighteen n’s, sixteen o’s, one p, one q, six r’s, twenty-seven s’s, twenty-one t’s, three u’s, seven v’s, eight w’s, three x’s, four y’s, and one z.
1982 年， Scientific American 月刊上刊登了一个 autogram 杰作：
Only the fool would take trouble to verify that his sentence was composed of ten a’s, three b’s, four c’s, four d’s, forty-six e’s, sixteen f’s, four g’s, thirteen h’s, fifteen i’s, two k’s, nine l’s, four m’s, twenty-five n’s, twenty-four o’s, five p’s, sixteen r’s, forty-one s’s, thirty-seven t’s, ten u’s, eight v’s, eight w’s, four x’s, eleven y’s, twenty-seven commas, twenty-three apostrophes, seven hyphens and, last but not least, a single !
奇妙的心电图数列
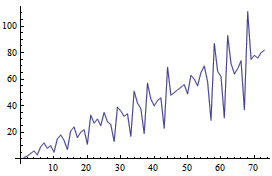
心电图数列 (EKG Sequence) 的定义简单而有趣：第一项为 1 ，第二项为 2 ，以后的每一项都是最小的和前一项不互质并且不曾出现过的数。换句话说，数列 a(1)=1 ， a(2)=2 ，且当 n>2 时取 a(n) 为所有满足以下两个条件的数中最小的那一个：该数与 a(n-1) 有大于 1 的公约数，并且该数与前面 n-1 项都不相等。心电图数列的前面 20 项为
1, 2, 4, 6, 3, 9, 12, 8, 10, 5, 15, 18, 14, 7, 21, 24, 16, 20, 22, 11 …
为什么它叫做心电图数列呢？原因很简单——因为把它描绘在图象上时，看上去像一张心电图。
