我喜欢各种各样的证明。有史以来我见过的最诡异的证明写在http://www.matrix67.com/blog/article.asp?id=34。人们很难想到这样一些完全找不到突破口的东西竟然能够证明得到。说“没有突破口”还不够确切。准确地说,有些命题多数人认为“怎么可能能够证明”却用了一些技巧使得证明变得非常简单。我看了五色定理的证明,定理宣称若要对地图进行染色使得相邻区域不同色,五种颜色就够了。没看证明之前,我一直在想这个玩意儿可以怎么来证明。直到看了证明过程后才感叹居然如此简单,并且立即意识到四色定理基本上也是这种证明方法。还有,像“一个单位正方形里不可能包含两个互不重叠且边长和超过1的小正方形”这样的命题竟然完全用初中学的那些平面几何知识证明到了,简单得不可思议。关键是,我们能够读懂证明过程,但只有牛人才能想到这个证明过程。
今天在OIBH上看到了这个帖子,帖子中哲牛分享的一篇文章The Power Of Mathematics恰好说明了这一点。文章中包含有一个推翻“万物皆数”的新思路,相当有启发性。今天我想把我已经知道的四种证明连同新学到的这一个一起写下来。
如何证明存在一种不能表示为两个整数之比的数?
古希腊曾有“万物皆数”的思想,这种认为“大自然的一切皆为整数之比”的思想统治了古希腊数学相当长的一段时间,许多几何命题都是根据这一点来证明的。当时的很多数学证明都隐性地承认了“所有数都可以表示为整数之比”,“万物皆数”的思想是古希腊数学发展的奠基。直到有一天,毕达哥拉斯的学生Hippasus告诉他,单位正方形的对角线长度不能表示为两个整数之比。被人们公认的假设被推翻了,大半命题得证的前提被认定是错的,古希腊时代的数学大厦轰然倒塌,数学陷入了历史上的第一次危机。最后,Eudoxus的出现奇迹般地解决了这次危机。今天我们要看的是,为什么单位正方形的对角线长度不能表示为两个整数之比。
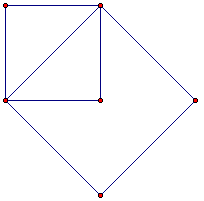
单位正方形的对角线长度怎么算呢?从上面的这个图中我们可以看到,如果小正方形的面积是1的话,大正方形的面积就是2。于是单位正方形的对角线是面积为2的正方形的边长。换句话说,Hippasus认为不可能存在某个整数与整数之比,它的平方等于2。
中学课程中安排了一段反证法。当时有个题目叫我们证根号2是无理数,当时很多人打死了也想不明白这个怎么可能证得到,这种感觉正如前文所说。直到看了答案后才恍然大悟,数学上竟然有这等诡异的证明。
当然,我们要证明的不是“根号2是无理数”。那个时候还没有根号、无理数之类的说法。我们只能说,我们要证明不存在一个数p/q使得它的平方等于2。证明过程地球人都知道:假设p/q已经不能再约分了,那么p^2=2*q^2,等式右边是偶数,于是p必须是偶数。p是偶数的话,p^2就可以被4整除,约掉等式右边的一个2,可以看出q^2也是偶数,即q是偶数。这样,p也是偶数,q也是偶数,那么p和q就还可以继续约分,与我们的假设矛盾。
根号2是无理数,我们证明到了。根号3呢?根号5呢?你可能偶尔看到过,Theodorus曾证明它们也是无理数。但Theodorus企图证明17的平方根是无理数时却没有继续证下去了。你可以在网上看到,Theodorus对数学的贡献之一就是“证明了3到17的非平方数的根是无理数”。这给后人留下了一个疑问:怪了,为什么证到17就不证了呢?一个俄国的数学历史家“猜”到了原因。
他猜测,当时Theodorus就是用类似上面的方法证明的。比如,要证明根号x不是有理数,于是p^2=x*q^2。我们已经证过x=2的情况了,剩下来的质数都是奇数。如果x是奇数且p/q已经不能再约分,那么显然p和q都是奇数。一个奇数2n+1的平方应该等于4(n^2+n)+1,也即8 * n(n+1)/2 + 1,其中n(n+1)/2肯定是一个整数。如果p=2k+1,q=2m+1,把它们代进p^2=x*q^2,有8[k(k+1)/2 – x*m(m+1)/2] = x-1。于是x-1必须是8的倍数。如果当时Theodorus是这么证明的,那么他可以得到这样一个结论,如果x-1不能被8整除,那么它不可能被表示成(p/q)^2。好了,现在3、5、7、11、13减去1后都不是8的倍数,它们的平方根一定不是有理数。在x=9时发生了一次例外,但9是一个平方数。而当x=17时这种证明方法没办法解释了,于是Theodorus就此打住。
实际上,我们上面说的这么多,在古希腊当时的数学体系中是根本不可能出现的。毕达哥拉斯时代根本没有发展出代数这门学科来,它们掌握的只是纯粹的几何。因此,Hippasus当时的证明不可能像我们现在这样搞点什么奇数x偶数y之类的高科技东西。事实上,Hippasus当时完全运用的平面几何知识来证明他的结论。有人觉得奇怪了,既然当时没有代数,古希腊人是怎么提出“所有数都可以表示为整数之比”的呢?其实古希腊人根本没有提出什么整数之比,这是后人的一个误解。当时毕达哥拉斯学派提出的,叫做“公度单位”。
两条线段的公度单位,简单的说就是找一个公度量,使得两条线段的长度都是这个公度量的整倍数(于是这个公度量就可以同时作为两条线段的单位长度并用于测量)。寻找公度量的方法相当直观,就是不断把较长的那个线段减去短的那个线段,直到两个线段一样长。熟悉数论的同学一下就明白了这就是欧几里德的辗转相除算法求最大公约数。第一次数学危机的根结就在于,古希腊人理所当然地相信不断地截取线段,总有一个时候会截到两个线段一样长。后来,Hippasus画了这么一张图,告诉大家了一个反例:有可能这个操作会无穷尽地进行下去。
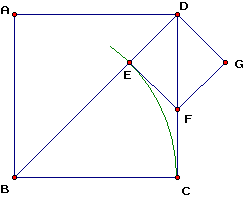
现在看他怎么解释,在图中的BC和BD之间进行辗转相除为什么永远不能停止。把BD减去BC,剩下一段DE。以DE为边做一个新的小正方形DEFG,那么显然DE=EF=FC(∵△EDF为等腰直角且△BEF≌△BCF)。接下来我们应该在BC和DE间辗转相除。BC就等于CD,CD减去一个DE相当于减去一个FC,就只剩下一段DF了。现在轮到DE和DF之间辗转相除,而它们是一个新的正方形的边和对角线,其比例正好与最初的BC和BD相当。于是,这个操作再次回到原问题,并且无限递归下去。最后的结论用我们的话说就是,不存在一个数x使得BC和BD的长度都是x的整倍数。于是,BD/BC不能表示为两个整数之比p/q(否则BD/p=BC/q,这就成为了那个x)。
有发现上面的代数证明和几何证明之间的共同点吗?它们都是这样的一个思路:假设我已经是满足这个性质的最小的那个了,那么我就可以用一种方法找出更小的一个来,让你无限循环下去,数目越来越小,永