著名的四色定理（four color theorem）告诉我们，如果一个地图由若干个连通区域构成（没有飞地），那么在给每个区域染色时，为了让相邻区域的颜色不同，最多只需要四种颜色就足够了。不过，这个结论成立有一个条件：整个地图已经事先确定了。如果我们每次只增加一个区域的话呢？具体地说，如果每次你给一个区域染色之后，我再画出下一个区域，并且之前已经染好颜色的区域不能再修改了，那么四种颜色还足够吗？这里，我们假设，在染色时，你总是遵循一个非常朴素的贪心策略：用第一个合法的颜色给每个新的区域染色。下面这个例子告诉我们，在这些假设下，四种颜色就不够了，有时五种颜色是必需的。
我们的问题就是，在这些假设下，五种颜色就一定够吗？有没有可能构造出某个情况，使得六种颜色是必需的？有没有可能构造出某个情况，使得七种颜色是必需的？
看守打算和 A 、 B 两名囚犯做一个游戏。首先，看守从一副牌中取出大小王，将剩余的 52 张牌洗好，并在桌子上从左至右地把它们摆成一排，每张牌都是正面朝上。然后，看守让囚犯 A 来到桌前，允许囚犯 A 观察牌面，并交换其中两张牌的位置。接着，看守将囚犯 A 关回牢房，把所有牌全都翻到背面朝上（但位置不变），让囚犯 B 来到桌前。看守随便报出一张牌的花色和点数（比如“梅花 3”），要求囚犯 B 找出这张牌。囚犯 B 每次可以翻开任意一张尚未翻开的牌，但一共只有 26 次机会。如果囚犯 B 在这 26 次机会之内找到了看守想要的牌，则两名囚犯赢得游戏，无罪释放；如果囚犯 B 翻开了 26 张牌之后，还没找到看守想要的牌，则两名囚犯输掉游戏，立即死刑。在整个游戏开始之前，两名囚犯可以商量一个策略；游戏开始后，两人就不能有任何其他形式的交流。果不其然，这又是一个关满了数学天才的监狱。两名囚犯碰头后，很快就商量出了一种必胜的策略。这种必胜的策略是什么？
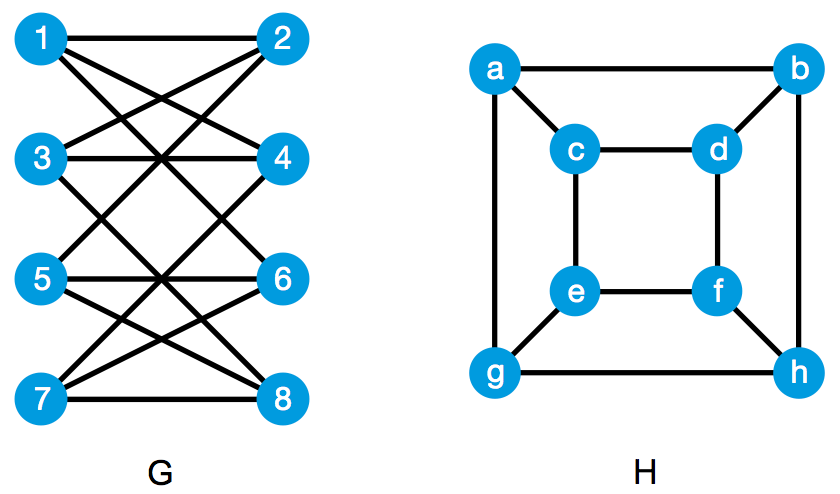
若干个顶点（vertex）以及某些顶点对之间的边（edge）就构成了一个图（graph）。如果图 G 和图 H 的顶点数相同，并且它们的顶点之间存在着某种对应关系，使得图 G 中的两个顶点之间有边，当且仅当图 H 中的两个对应顶点之间有边，我们就说图 G 和图 H 是同构的（isomorphism）。直观地说，两个图是同构的，意思就是它们本质上是同一个图，虽然具体的画法可能不一样。下面的两个图就是同构的。其中一种顶点对应关系是： 1 – a, 2 – c, 3 – d, 4 – b, 5 – e, 6 – g, 7 – h, 8 – f 。
目前，人们还没有找到任何高效的算法，能迅速判断出两个图是否同构。在普通计算机上，判断两个图是否同构，这需要花费大量的时间。因此，人们经常以图的同构为例，来解释复杂度理论和现代密码学中的诸多概念。
假设你家里的计算机十分强大，能很快判断出两个图是否同构，还能在两个图确实同构的情况下，给出一种顶点对应关系。但你的同桌家里的计算机却非常弱，没法做什么大型运算。课堂上，老师向全班展示了两个很复杂的图，不妨把它们叫作图 G 和图 H 。老师布置了一个特别的选做题：判断出这两个图是否同构。每个同学都可以提交答案，答案里只需要写“是”或者“不是”即可。按时提交答案并答对者，期末考试会获得 5 分加分；按时提交答案但答错了的，期末考试成绩将会倒扣 30 分；不参与此活动的同学，期末考试既不加分也不扣分。显然，每个同学都不敢随意提交答案，除非百分之百地能保证自己获得的答案是正确的。回到家后，借助家里的超级计算机，你很快判断出了这两个图是同构的。你给你的同桌发送了信息：“我已经算出来了，这两个图是同构的。”但是，你的同桌却回复说：“你不会是骗我的吧？”你打算怎样说服他，这两个图确实是同构的呢？
ASCII 编码已经是非常直观了。 65 号字符就是大写字母 A ， 66 号字符就是大写字母 B ，以此类推， 90 号字符就是大写字母 Z 。为了看出某个编码究竟对应字母表中的第几个字母，我们只需要用下面的函数关系即可：
f(x) = x - 64
整个函数关系极其简单，里面只包含一个数学运算符号。
当然，历史上也出现过很多非常不直观的字符编码方式。 EBCDIC 是由 IBM 提出的一种字符编码标准，它的编码方式十分古怪，可害苦了当年的那些程序员。据说，当年的程序员没有一个不痛恨 EBCDIC 的。因此， EBCDIC 也理所当然地成为了众人调侃的对象。 Wikipedia 上的 EBCDIC 页面甚至还专门有一节，讲述各种与 EBCDIC 有关的笑话。有一个经典的笑话说的就是，美国政府跑去 IBM ，想要研发一种数据加密标准，于是 EBCDIC 编码就诞生了。经典游戏 Zork 中， EBCDIC 也被用来形容艰涩难懂的文字：
一个大房间里，各式各样笨重的机器在呼呼作响，电阻烧焦了的味儿扑鼻而来。其中一面墙上有三个按钮，形状分别是圆形、三角形和正方形。自然，这些按钮上方的说明文字都是用 EBCDIC 书写的……
下面这道题目是 Using your Head is Permitted 谜题站 2015 年 12 月的题目。
若干个顶点（vertex）以及某些顶点对之间的边（edge）就构成了一个图（graph）。下面就是这篇文章里会用到的四个图。其中，第一个图是由 2 个顶点组成的路径（path），因而我们把它称作 P2 ；第二个图是由 3 个顶点组成的路径，因而我们把它称作 P3 。第三个图是由 3 个顶点组成的一个环（cycle），因而我们把它称作 C3 ；第四个图是由 4 个顶点组成的一个环，因而我们把它称作 C4 。
选取图中的一个或多个顶点，同时选出这些顶点之间的所有边，得到的就是原图的一个“诱导子图”（induced subgraph）。在这篇文章中，我们只考虑那些连通的诱导子图。下面是一个有 6 个顶点的图，右边则列出了由它可以产生出来的所有连通诱导子图。注意，由于有些诱导子图不是连通的（比如只选择正上方的两个点和右下角的两个点，或者干脆只选择最左边那个点和最右边那个点），因而它们并没有在右边列出。在这些连通诱导子图里，很多图的本质都是相同的。比方说，第一行最后三个图和第二行前面四个图的本质是一样的，它们都是刚才我们介绍过的 P2 。当然，第一行的前六个图的本质也都是一样的，即由单个顶点构成的图，有时会被人们记作 K1 。观察最后一行的倒数第二个和倒数第三个图，你能看出这两个图的本质也一样吗？只不过，它们就没有什么固定的名字了。在这些连通诱导子图里，哪一种图出现的次数最多呢？答案就是 P3 ，它一共出现了 8 次。
我们的问题是：能否构造一个图，使得里面出现次数最多的连通诱导子图是 C3 ？能否构造一个图，使得里面出现次数最多的连通诱导子图是 C4 ？注意，如果两种连通诱导子图出现的次数一样多，那它们都不算出现次数最多的连通诱导子图。