下图中的三个绳圈套在一起，没有哪一个绳圈能从中分离出来。不过，真正有趣的是，如果去掉其中任意一个绳圈，那么其他所有的绳圈都全部散开了。如果 n 个绳圈套在一起，并且任意去掉其中一个绳圈都会同时解开其他所有套着的绳圈，我们就把它叫做 n-component Brunnian link 。
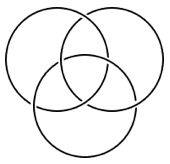
你能想出一个 n = 4 的 Brunnian link 吗？ n = 5 呢？ n 可以任意大吗？
趣题
IMO2012趣题：带有说谎的猜数游戏
考虑一个传统的猜数游戏。 A 、 B 两名玩家事先约定一个正整数 N ，然后 A 在心里想一个不超过 N 的正整数 x ， B 则需要通过向 A 提问来猜出 A 心里想的数。 B 的问题只有唯一的格式：先列出一些数，然后问 A “x 是否在这些数里”， A 则需要如实回答“是”或者“否”。显然， B 是保证能猜到 x 的，只需要依次询问“x 是否等于 1 ”，“x 是否等于 2 ”即可。由于 B 可以精心选出满足某种特征的所有数，询问 x 是否在这些数里，因而 B 还可以做得更好。例如当 N ＝ 16 时， B 第一次可以问“x 是否小于等于 8 ”，或者等价地，“x 是否属于 {1, 2, 3, 4, 5, 6, 7, 8} ”；接下来，根据 A 的回复继续细问“x 是否小于等于 4 ”或者“x 是否小于等于 12 ”，以此类推。另一种方法则是询问“x 的二进制表达的第一位是否是 1”，“x 的二进制表达的第二位是否是 1”，以此类推，从而获得 x 的二进制表达的所有数位，便能推出 x 来。
现在，有意思的问题来了。假设 A 可以偶尔说谎（但保证不会连续说谎两次），那么 B 还能通过询问猜出 A 所想的数吗？如果愿意的话， B 可以询问任意多次。
几个精彩的数论问题
从同事那里借来了一本单墫教授主编的《初等数论》奥数书，看到很多精彩的问题，在这里做个笔记，与大家一同分享。不少问题和答案都有过重新叙述，个别问题有所改动。
问题：找出所有使得 2n – 1 能被 7 整除的正整数 n 。
答案：由于 2n 的二进制表达为 1000…00 （n 个 0），因此 2n – 1 的二进制表达为 111…11 （n 个 1）。而 7 的二进制表达是 111 ，要想让它整除 n 个 1 ，显然 n 必须是也只能是 3 的倍数。
趣题：构造多边形使得过边界上某一点的任意直线均能等分面积
这是 2008 年莫斯科数学竞赛中的一个问题。构造一个多边形，使得这个多边形的边界上存在这样的一个点 O ：经过点 O 的任意直线均会把该多边形分成面积相等的两部分。这看起来不大可能对吧？但其实构造却并不困难。你能想出来吗？
趣题：把矩形分割为面积相同但形状各不相同的小矩形
Using your Head is Permitted 数学谜题站的主持人 Michael Brand 某日收到了来自 R. Nandakumar 的一个谜题：是否有可能把一个矩形剖分成若干个小矩形，使得每个小矩形的形状互不相同，但它们的面积都一样？没有想到，从这个问题出发，加上一些非常机智巧妙的分析与构造，我们能得到越来越多有意思的东西。于是，它就变成了 Using your Head is Permitted 今年 3 月的谜题。看了谜题的答案后，我也被彻底折服，决定把这一系列的思考重述在此，和大家一同分享。为了简便起见，下面的“矩形剖分方案”一律指的是把一个大矩形分割成若干个小矩形的方案。