证明:对于任意一个三角形和任意一个大于等于 4 的正整数 n ,都存在一种把这个三角形分割成 n 个等腰三角形的方案。这个问题曾经出现在 1976 年的 Crux Mathematicorum 上。 1977 年, Gali Salvatore 给出了一个非常漂亮的解答。
趣题
IMO2010趣题:用有限次操作得到2010^(2010^2010)枚硬币
下面这个问题来自于 IMO 2010 中的第 5 题。桌子上有 B1 、 B2 、 B3 、 B4 、 B5 、 B6 共六个盒子,初始时每个盒子里面都有一枚硬币。允许以下两种操作:
(1) 选择一个非空的盒子 Bj (1 ≤ j ≤ 5),从 Bj 里拿走一枚硬币,然后在 Bj+1 里添加两枚硬币。
(2) 选择一个非空的盒子 Bk (1 ≤ k ≤ 4),从 Bk 里拿走一枚硬币,然后交换 Bk+1 和 Bk+2 里面的硬币数(这两个盒子里的硬币数都有可能是 0 )。
是否有可能通过有限次操作,使得最后 B1 、 B2 、 B3 、 B4 、 B5 都是空的,并且 B6 里面恰好有 2010 ^ (2010 ^ 2010) 枚硬币(符号 ^ 表示乘方)?
趣题:一个与含60度的三角形有关的性质
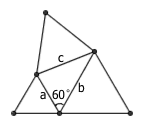
有一个三角形,三边长分别为 a 、 b 、 c ,其中 a 、 b 两条边夹角为 60° 。分别以 a 、 b 、 c 为边向外作等边三角形。求证:前两个等边三角形的面积之和,减去第三个等边三角形的面积,将等于原三角形的面积。
趣题:测量两根木棒长度的更优方案
这道题出自 Fifty Challenging Problems in Probability 一书中的第 49 个问题(有趣的是,这本书里其实一共有 56 个问题)。假设你有一个长度测量工具。在测量实际长度为 L 的物体时,由于不可避免的误差,你将会得到一个平均值为 L ,方差为 σ2 的随机结果。现在有两根长度未知的木棒,你需要用两次测量得出每根木棒的长度,使得所得结果的误差尽可能的小。除了分别测量每根木棒的长度以外,还有没有什么更好的方案?
趣题:证明边权递增的路径始终存在
一个树林里有 100 个村庄,它们之间有 1000 条小路,每条小路都连接着两个不同的村庄。每条小路 e 都有一条难度系数 l(e) ,所有小路的难度系数都不相同。现在有一个探险家,他想要选择一条长度为 20 的路径,使得所经过的小路的难度系数不断增加。求证:他总能找到这样的路径。
探险家可以任意选择路径的起点和终点。