今天看到了一道很有趣的几何题。如图，四边形 ABCD 中，连接对角线 AC 、 BD ，若 ∠ABD = 40° ， ∠ADB = 80° ， ∠CBD = 70° ， ∠CDB = 50° ，求 ∠BAC 的度数。
这道题看上去似乎非常简单，但稍作尝试你就会发现，仅仅是在这几个角度之间来回倒腾，是没法求出 ∠BAC 的度数的。听说过 Langley 问题（就是那个臭名昭著的 20-80-80 三角形）的人就会知道，这种类型的题目往往会非常非常地复杂。据说这是 1989 – 1990 年加拿大亚伯达省中学数学竞赛中的一道题目，当时只有一个人做对，并且解答过程用到了非常繁琐的三角函数运算。然而，这道题实际上有一个非常漂亮的秒杀方法，完全不需要使用三角函数。你能想到吗？
日常生活中经常会出现这样的场景：你想在数据库上查询某个东西，但却不希望留下线索，让别人知道你查询了什么。比方说，投资人可能会在数据库上查询某支股票的信息，但却不希望任何人知道他感兴趣的股票究竟是哪一支。看上去，似乎唯一的办法就是把整个数据库全部拷回家。然而，这些数据往往都拥有非常庞大的体积，全部拷走通常都是很不现实的；另外，考虑到数据内容的隐私性和数据本身的宝贵价值，数据的持有者通常也不允许其他人把整个数据全盘拷走。不过，随着分布式数据库的广泛应用，上面的难题有了一个两全其美的好办法：假设有两个内容完全相同的数据库，投资人可以先在第一个数据库上执行一个不会透露目的的查询，再在另一个数据库上执行另一个不会透露目的的查询，两次查询结合起来便能推出想要的结果。只要没有人刻意去收集并且对比两个数据库的查询记录，那么谁也不会知道投资人真正想要查询的是什么。在这个背景下，我们有了下面这个有趣的问题。
服务器随机产生了一个 {1, 2, …, 100} 的子集 S ，并且同时发送给了 A 和 B 两名前台工作人员。 A 、 B 两名前台都接受其他人的提问，但为了保护数据，两个人都只能用“是”或者“否”来回答问题，并且都不允许同一个人重复提问。你非常关心某个数 n 是否在这个子集里。其实，你本来可以直接问 A 和 B 中的任何一个人“数字 n 是否在集合 S 里”，但是这样一来，对方就知道了你想要查询的是什么。为此，你可以向 A 和 B 各问一个问题（结合两人的回答便能推出集合 S 里是否包含数字 n ），但却不能让 A 和 B 当中的任何一个人知道你查询的是哪个数（我们假设 A 、 B 两人不会串通起来，把他们各自收到的问题联系在一起）。事实上，你需要保证 A 和 B 两人都不能从你的问题中获取到任何信息，也就是说，对于 A 和 B 当中的任何一个人来说，各种问题出现的概率不会随着 n 值的改变而改变。再换句话说，如果 n 的值变了，那么 A 和 B 各自将会听到的问题应该拥有和原来相同的概率分布。
下面是趣题集 Which Way Did the Bicycle Go 中的第 71 个问题。如下图，在这个六边形的围墙中，如果站在图中圆点的位置，那么有两面墙不能被完全看见（其中一面墙完全看不见）。能否设计出一个多边形围墙，使得站在围墙里面的某个地方后，所有的墙都至少有一部分是不可见的？
下面是 IBM Ponder This 2013 年 5 月的谜题：写一个程序来计算 f(x) = 1 + x + x2 + x4 (mod 2233393) 。你的程序只能使用以下三种语句，其中等号表示赋值，变量 2 和变量 3 的位置都可以用常量来代替：
(1) 变量 1 = 变量 2 + 变量 3
(2) 变量 1 = 变量 2 * 变量 3
(3) 变量 1 = 变量 2 mod 变量 3
很容易想到，一种最基本的解法如下：
a = x * x
b = a * a
c = a + b
d = c + x
e = d + 1
f = e mod 2233393
这道谜题则要求你找到另外一种解法，它必须同时满足下面两个额外的要求：
(1) 最多使用两次变量与变量之间的乘法运算（但允许多次变量与常量之间的乘法运算）
(2) 最后两次运算分别是一次变量与变量之间的乘法运算和一次取余运算
通信复杂度（communication complexity）主要研究这么一类问题： A 持有数据 x ， B 持有数据 y ，他们想要合作计算某个关于 x 和 y 的二元函数值 f(x, y) ，那么在渐近意义下，两人至少需要传输多少 bit 的数据。最近着迷于通信复杂度，看到了几个与通信复杂度有关的问题，和大家分享一下。下面就是其中之一。
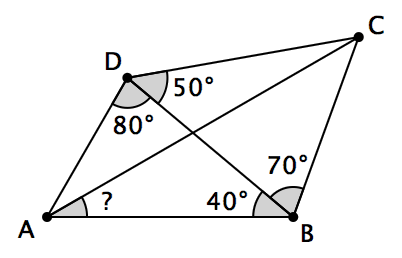
A 、 B 的手中各有一个 {1, 2, …, n} 的子集。两人想知道，如果把他们手中的数全都放在一块儿，那么这些数（可能会有重复的数）的中位数是多少。然而， A 、 B 两人远隔千里，他们之间通信的成本非常高。因此，他们想在通信线路上传输尽可能少的信息，使得最终两人都知道中位数的值。在这里，为了简便起见，我们直接定义 m 个数的中位数是第 ⌈ m / 2 ⌉ 小的数，因而如果 m = 2k ，那么中位数就应该直接取第 k 小的数。
其中一种最笨的方法是， A 把手中的所有数全部发给 B 。由于发送一个不超过 n 的正整数最多会用到 log(n) 个 bit ，而 A 手里的数最多有 O(n) 个，因此 A 传给 B 的信息量就是 O(n · logn) 。于是， B 就得到了足够多的信息，可以直接计算中位数了，算好后再把结果告诉 A ，此时又要耗费 log(n) 个 bit （但它并不会成为通信量的瓶颈）。因此，在这种方案中，总的通信复杂度就是 O(n · logn) 。事实上，传送一个 {1, 2, …, n} 的子集只需要一个 n 位 01 串就够了，因而我们可以把通信复杂度降低到 O(n) 个 bit 。
利用下面的办法，我们可以实现 O(logn · logn) 的通信复杂度。首先， A 、 B 分别告诉对方自己手中有多少个数，这一共会耗费 O(logn) 个 bit 。接下来，两人在区间 [1, n] 上进行二分查找。假设到了某一步，中位数被限定在了区间 [i, j] 里，那么 A 就计算出 k = (i + j) / 2 ，数一数自己手中有多少个数比 k 小，然后告诉 B ，由 B 再来数数自己这边又有多少个比 k 小的数，从而判断出 k 作为中位数来说是偏大了还是偏小了，并把判断出来的结果返回给 A 。根据情况，区间 [i, j] 将被更新为 [i, k] 或者 [k, j] ，两人在新的区间上继续二分下去。整个算法将会持续 O(logn) 轮，每一轮都会传输 O(logn) 的数据，因此总的通信复杂度是 O(logn · logn) 。
另一方面，通信复杂度至少是 Ω(logn) 的。这是因为，如果规定 A 和 B 最多只能交流 k 个 bit ，那么整个交流历史最多就只有 k 次分岔的机会，到最后最多只能产生 2k 个不同的分支；但事实上中位数有可能是 1 到 n 中的任何一个，共有 n 种不同的可能，因此 2k 必须大于等于 n 。这说明 k 必须大于等于 log2(n) ，也就是说两个人总会有必须要交流 log2(n) 个 bit 才行的时候。
一个有意思的问题自然而然地诞生了：我们所得的上界和下界仍然有差距。究竟是刚才的算法还不够经济，还是刚才证明的结论还不够强呢？
还想说明一点的是，两个人商量算法的过程，或者其中一个人把算法告诉另一个人的过程，这可以不算进通信复杂度里。事实上，把它们算进通信复杂度里也没关系，因为它们反正都是 O(1) 的。