最近在忙很多事情，抱歉很久没更新了。刚才抽时间上网闲逛，在reddit上看到了一个叫做The Hoeflin Power Test的网页，里面的大多数题目都是我从来没见过的、题目描述简单的、一般性极强的数学问题，无聊时从里面找一两道来，足以打发一整天的时间。从这个网站出发，我还顺藤摸瓜地找到了其它一些有如天书般的智商测试题目（尤其是那个图形测试），据称是专门用于测试最罕见的高智商人群的，足够大家在这个周末折磨一下自己了。
Strict Logic Sequences Examination – Form I 数字规律1
Strict Logic Sequences Examination – Form II 数字规律2
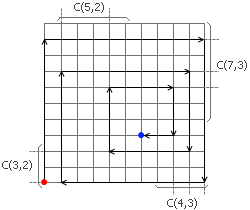
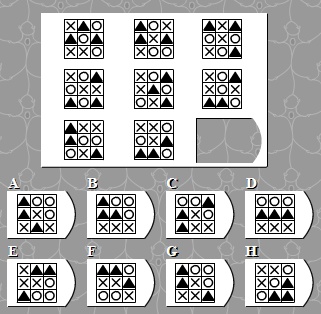
Strict Logic Spatial Examination 48 图形规律，有3页
eMiT 类比推理
查看更多：
http://www.eskimo.com/~miyaguch/hoeflin.html
http://www.iq-tests-for-the-high-range.com/
大学生活混起来很快，不知不觉又是一年过去了。去年5月10日的ACM校内赛给我留下了许多美好的回忆，因此今年我主动去报了名（上次是被人给拖去的）。今年有点装怪，题目数量不变，但时间缩短为4个小时。原计划是从8:00做到12:00，结果可能是因为我们所在的7号机房迟迟没有开门，时间临时改成了8:15到12:15。总的来说，今年的题目比去年要糟糕得多，但也不乏一些精彩的题目。
和去年一样，第一题依旧是所有题目中最科学的一道。题目给定一个不超过2000*2000的网格，你在最左下角的位置（即(0,0)点），你的目的地在(x,y)。要求你的路线不得经过同一个交叉点两次，且不允许左转（题目背景让这个条件顺理成章：街道靠右行，左转不方便），问合法的路线共有多少种。题目难点就是你不一定要走最近的路，完全允许你绕上一大圈；这破坏了有序性，很难构造出递推公式或动态规划模型。稍微画一下图，我们发现了一些显然但很有启发性的规律：每一次右转后，你左手边方向的所有区域都不能再走了，这很可能产生出规模更小的子问题来。另外，所有合法路线必然是有如螺旋线一样的一圈一圈绕着终点走，这种隐藏的有序性也为动态规划提供了可能。但顺着这个思路想下去屡屡碰壁，我猜不少队伍都卡在这儿了吧。
后来我完全打翻前面的全部思路，猛然想到了一个具有决定意义的想法：街道的选取唯一地决定了整个路线。例如，假设我想计算转弯恰好11次的路线有多少条。这样的路线一定含有三条向上走的路、三条向右走的路、三条向下走的路和三条向左走的路。除去第一条路和最后一条路的位置都是确定的，其它的路选在哪一行或者哪一列唯一地决定了整个路线。因此，我们可以用排列组合直接计算出答案来。向上走的路是五选二，向右走的路是七选三，向下走的路是四选三，向左走的路是三选二。把它们各自的选取方案数乘起来就得到了拐弯11次的合法路径。于是，计算所有的路线数只需要从小到大枚举拐弯的次数，每一次计算都是常数的，总复杂度是O(n)的；整个算法的瓶颈反倒是O(n^2)的组合数预处理，不过这个复杂度完全可以承受。
网友Qian Yongchao发来邮件说，他在阅读当前正大红大紫的一本书叫做Outliers。书中谈到IQ测试时，作者提到了Raven’s Progressive Matrices测试法。这是一系列从易到难的题目，一般有48道题。为了说明这种测试可以有多难，作者给出了整个测试的最后一道题，这道题目即使作者自己也不知道该怎么做。我在网上搜索了一下，确信书上印的题目是错误的。其实，那道题就是iqtest.dk上的那个火星IQ测试的最后一题。这个题确实很难，无数人都卡在这上面死活想不明白。
摘录几道题目。
计算1·2^2 + 2·3^2 + 3·4^2 + … + 19·20^2
原式 = (1^3 + 2^3 + … + 20^3) – (1^2 + 2^2 + … + 20^2) = 44100 – 2870 = 41230
求2^x = 3^y – 1的所有正整数解
x=1时(1,1)是一个解；当x>1时，方程模4后左边永远等于0，右边则是(-1)^y – 1，可知y为偶数。令y=2z，那么有2^x = (3^z – 1)(3^z + 1)，这就要求3^z-1和3^z+1都是2的幂；但它们只相差2，因此它们只有可能是2和4，于是z=1，即原方程的另一个解为(3,2)。
圆周上有2008个点。选择两个点连成一条线，再选另外两点连一条线，这两条线段相交的概率为多少？
给定四个点，在三种连接方案中恰有一种会发生相交。取遍所有C(2008,4)种组合，相交的总情况数总是占了1/3，因此所求的概率就是1/3。
小学四年级数学 第二学期期末测试题
(时间：90分钟 总分：100分)
一、直接写得数(每题0.5分，共10分)
32.8＋19＝ 0.51÷17＝ 240÷30＝ 1000×0.8＝
3.06＋0.2＝ 0.67＋1.24＝ 8×125＝ 7－6.28＝
8.2－0.01＝ 99×23＝ 50×4＝ 5÷1000＝
0.42＋9.5＝ 65×25×4＝ 0.08÷100＝ 10×0.5＝
1.82－0.63＝ 4.5＋1.5＝ 1－0.63＝ 231－99＝
二、填空(每空1分，共15分)
1．一个数，亿位上是6，百万位上是4，十万位上是5，千位上是8，其余各位上都是0，这个数写作( )，读作( )，最高位的计数单位是( )．
2．三百二十三亿六千八百七十万，写作( )，改写成用“亿”作单位的数约是( )．
3．25米60毫米＝( )毫米
4．3.45平方米＝( )平方米( )平方分米
5．150分＝( )时( )分
6．15吨60千克＝( )千克
7．自然数和0都是( )数．
8．在
、
、
、
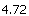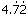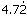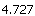这四个数中，最大的数是( )，最小的数是( )．