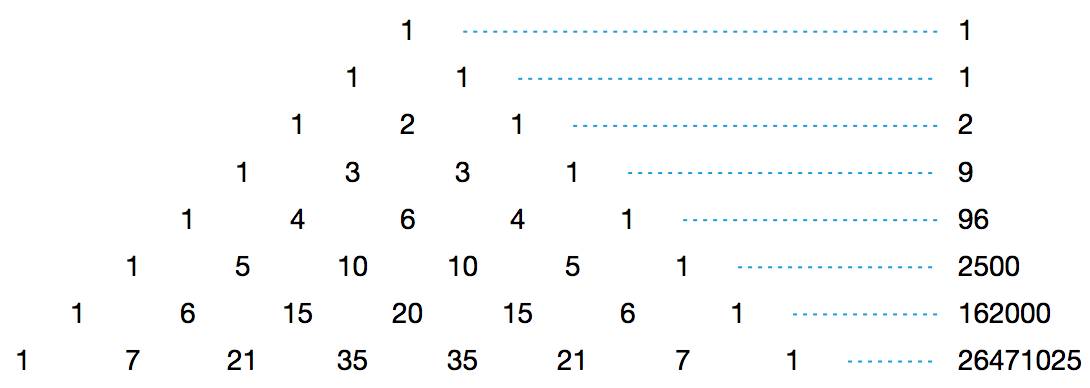
你相信吗,杨辉三角里竟然也有自然底数 e 的身影。 2012 年, Harlan Brothers 发现了杨辉三角中的一个有趣的事实。不妨把杨辉三角第 n 行的所有数之积记作 sn ,那么随着 n 的增加, sn · sn+2 / sn+12 会越来越接近 e ≈ 2.718 。事实上,我们有:
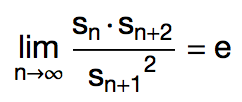
这是为什么呢? John Baez 在这个网页上给出了一个漂亮的解释。

你相信吗,杨辉三角里竟然也有自然底数 e 的身影。 2012 年, Harlan Brothers 发现了杨辉三角中的一个有趣的事实。不妨把杨辉三角第 n 行的所有数之积记作 sn ,那么随着 n 的增加, sn · sn+2 / sn+12 会越来越接近 e ≈ 2.718 。事实上,我们有:
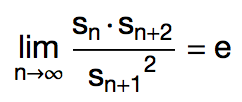
这是为什么呢? John Baez 在这个网页上给出了一个漂亮的解释。
保加利亚单人纸牌游戏(Bulgarian solitaire)的玩法如下:
取出 45 张牌,然后把它们随意分成若干堆。接下来,从每一堆里各取一张牌,叠在一起形成一堆新的牌。不断这样做下去,如果某个时候桌面上正好有 9 堆牌,并且各堆牌数分别为 1, 2, 3, 4, …, 9 ,你就获胜了。
乍看上去,如果初始局面设定不佳,游戏很可能会陷入某个循环,从而永远无法获胜。然而, 1981 年,丹麦数学家 Jørgen Brandt 证明了,对于任意一个初始局面(包括把所有牌摆成 1 堆,以及把所有牌分成 45 堆这样的极端局面),游戏都能在有限步之内获胜。事实上,如果把 45 换成任意一个三角形数 n = 1 + 2 + … + k ,结论仍然成立。
观察下面几个式子:
13 = 1; (1)2 = 1
13 + 23 = 9; (1 + 2)2 = 9
13 + 23 + 33 = 36; (1 + 2 + 3)2 = 36
13 + 23 + 33 + 43 = 100; (1 + 2 + 3 + 4)2 = 100
…… ……
大家应该可以猜到,事实上,对于任意正整数 n ,下述等式永远成立:
13 + 23 + … + n3 = (1 + 2 + … + n)2
这个恒等式的证明方法有很多很多,今天我看到了一种有趣的组合证明方法,来源于《Proofs that Really Count》的第 8 章。
问题:能否用多米诺骨牌既无重复又无遗漏地覆盖一个 6 × 6 的棋盘,使得棋盘上的每一条水平线和每一条竖直线都会穿过至少一个多米诺骨牌?举个例子,下图所示的棋盘覆盖方案就是不满足要求的,因为棋盘的第二条水平线不会切断任何一个多米诺骨牌。
