给定一个集合S和数n，从集合S中取出两个不同的数a,b满足a+b=n的总方案数叫做“集合S中关于n的互补数对个数”。是否有可能把全体非负整数划分为A、B两个集合，使得对于任意一个n，集合A和集合B中关于n的互补数对的个数都相同？

 
Read more…

如果一个矩形可以分割为若干个小矩形，每个小矩形都有至少一边为整数长，则原矩形同样有至少一个长度为整数的边。换句话说，用至少有一边的长度是整数的小矩形拼成一个大矩形，大矩形也有至少一条整数长的边。

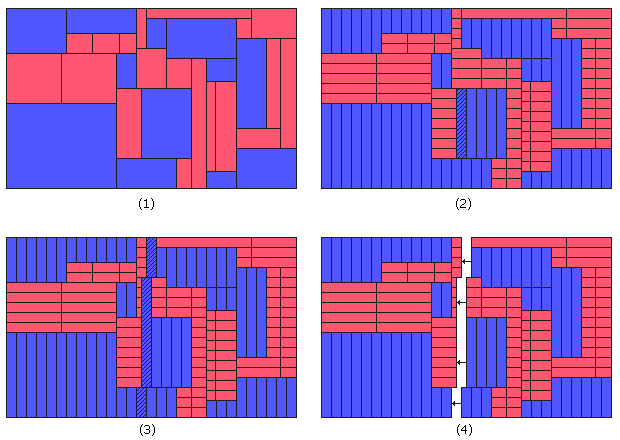
    我们首先把每个小矩形都分割成单位长或单位宽的长条。这样的话，大矩形里就只有两种小矩形：宽为1的（图(2)中的蓝色矩形）和高为1的（图(2)中的红色矩形）。我们对蓝色矩形的个数施归纳。随便选择一个蓝色的矩形（例如图(2)中的阴影矩形）。增加它的高度，让它“穿过”它头顶上的红色矩形（把它正上方的红色矩形截成左右两段），直到这根竖条状矩形的顶端碰到了另一个蓝色矩形的底端。把那个矩形作为新的操作对象，继续增加其高度（并可能再次更换“当前矩形”），直到达到整个大矩形的上边界。我们用同样的方法让最初所选的阴影矩形向下“生长”到大矩形的下边界。注意到在此过程中，蓝色矩形始终保持着单位宽度，红色矩形始终保持着单位高度。整个过程结束后，红色矩形变多了，但蓝色矩形的个数不变。此时我们得到了一条上下贯穿整个大矩形的蓝色矩形链。把它们擦掉，将右半部分左移一个单位，重新拼成一个大矩形。新的大矩形高度不变，宽度减一（因此原来的整数边还是整数，非整数边仍然不是整数），并且最关键的是蓝色矩形的个数减少了。反复进行这样的操作，总有一个时候大矩形里只剩下红色的矩形（则原大矩形高度显然为整），或者某次操作后所有矩形都被去掉了（则原大矩形宽度为整）。
    借用这种方法我们还可以得到一个有点搞笑的反证法。假设大矩形的横边竖边都不是整数。每一步操作后，这两个边仍然是非整数，这表明大矩形里不可能只剩一种颜色的小矩形，于是我们可以无限制地调用上面的操作。最后的结果是：我们得到了一个用整数长或整数宽的小矩形拼接而成的一个横边竖边都小于1的大矩形！这显然是荒谬的。

参考资料：http://www.cut-the-knot.org/Curriculum/Algebra/IntRectRobinson.shtml

    网友hetong_007在他的Blog上分享了几个“一句话证明”：

    在一个圆周上有若干个实数，将它们染成或红或蓝，满足红数等于左右两个相邻数的和，蓝数等于左右两个相邻数的和再除以2。求证，红色数的总和为零。
    我们用S红来表示所有红数的和，S蓝来表示所有蓝数的和，S表示所有数的和。于是不难得出S红+S蓝=S；S红+2S蓝=2S。

    定义f(x)满足：定义域及值域都是不为零的实数，且f(x)+f(y)=f(x·y·f(x+y))，求解f(x)。
    可知，在条件下y·f(x+y)≠1，于是f(x+y)≠1/y；令z=x+y，则f(z)≠1/(z-x)；对于每一个固定的z，x可以取任意非0实数，而它们所产生的1/(z-x)都不等于f(z)，那么f(z)只能等于1/(z-0)。经验证，答案满足条件。

    在一个平面上对所有点任意红蓝染色，求证一定存在两个自同色的相似凸n边形，满足相似比为e^pi。自同色是指自己的顶点都是一种颜色，两个凸n边形不一定要互相同色。
    在平面上做两个同心圆，且半径比为e^pi。在内圆上选2n-1个同色的点，分别与圆心连接，延长交于外圆。由鸽笼原理，外圆上的2n-1个点一定有n个点同色。

    网友B.Storm告诉我说，他正在写一个Mathematica的进阶教程。看这个趋势的话，这很可能会成为最强大的Mathematica中文教程了，希望能坚持写完。

    hetong_007发来邮件说，那位牛人在kloonigames把所有的原创游戏都列了出来。相当强大。

    网友Gestorm在TopLanguage里问到，如何构造一个[0,1]到(0,1)的一一映射。两个集合的势显然相等，它们之间一定有一个一一对应的函数。注意到(0,1)是[0,1]的子集，利用Cantor-Bernstein-Schroeder定理，只要我们能找到一个从[0,1]到(0,1)的单射函数，我们便找到了两个集合间的双射函数（因为上述定理的证明是构造性的）。这非常简单，例如f(x)表示x与0.5的平均数即可。考虑上述定理的Julius König证明，我们立即得到一个[0,1]到(0,1)的一一映射：f(0)=1/4, f(1/4)=3/8, f(3/8)=7/16, …，不断进行(x+1/2)/2的迭代；同样地，f(1)=3/4, f(3/4)=5/8, f(5/8)=9/16, …；对于其它所有未定义到的x，f(x)=x。这个函数显然是双射的。
    仔细观察这个函数。当你领会到这个函数的真谛时，你突然恍然大悟：我可以用类似地办法弄出无穷多个[0,1]到(0,1)的一一映射。例如，最简单的便是f(0)=1/2, f(1)=1/3；然后f(1/2)=1/4, f(1/3)=1/5, f(1/4)=1/6, …, f(1/i)=1/(i+2)；对于其它未定义的x，f(x)=x。
    查看TopLanguage的原帖可以看到一些类似的结果。

  
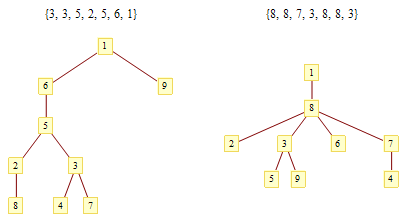
    Cayley公式是说，一个完全图K_n有n^(n-2)棵生成树，换句话说n个节点的带标号的无根树有n^(n-2)个。今天我学到了Cayley公式的一个非常简单的证明，证明依赖于Prüfer编码，它是对带标号无根树的一种编码方式。
    给定一棵带标号的无根树，找出编号最小的叶子节点，写下与它相邻的节点的编号，然后删掉这个叶子节点。反复执行这个操作直到只剩两个节点为止。由于节点数n>2的树总存在叶子节点，因此一棵n个节点的无根树唯一地对应了一个长度为n-2的数列，数列中的每个数都在1到n的范围内。下面我们只需要说明，任何一个长为n-2、取值范围在1到n之间的数列都唯一地对应了一棵n个节点的无根树，这样我们的带标号无根树就和Prüfer编码之间形成一一对应的关系，Cayley公式便不证自明了。
Read more…