想必搞OI/ACM的朋友都应该知道八皇后问题,这是学习编程的必修课程之一:在国际象棋棋盘上最多可以放置多少个互不攻击的皇后(皇后可以攻击它所在的行、列、对角线方向上的棋子)?显然,能够放置的皇后数不超过8个,因为国际象棋的棋盘一共就8行8列。事实上,放置8个互不攻击的皇后是有可能的,并且方法不止一种。
上个月的IBM Ponder This考虑了一个八皇后问题的扩展:最多可以在国际象棋棋盘上放置多少个皇后,使得每一个皇后最多只能攻击到一个其它的皇后?
证明
数学思维游戏两则:Gabriel喇叭、世界末日论
看到新词就上一下Wikipedia确实是一个好习惯。前一篇日志的那个pdf里作者提到了Gedankenexperiment(Thought experiment),上Wikipedia一查果然学到了牛B的新东西。好多物理定律其实完全是由思维实验推导出来的,难以置信仅仅是思考竟然就能得出物理世界遵从的各种法则。经典的物理思维实验有Newton大炮、Galileo斜塔实验、Schrödinger的猫猫、Maxwell的妖怪等等。还有,Turing机也是一个伟大的思维实验。

数学上的不少悖论(特别是涉及到维度和无穷的悖论)都是相当有趣的思维实验。Gabriel喇叭是y=1/x在[1,+∞)上的图象沿x轴旋转一周所形成的旋转体。这个简单的三维图形有一个奇特的性质:它的表面积无穷大,却只有有限的体积。为了证实这一点,只需注意到:
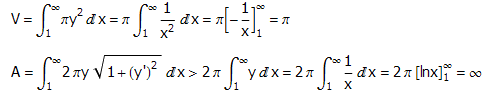
Gabriel喇叭会导出一个非常诡异的悖论:如果你想用涂料把Gabriel喇叭的表面刷一遍,你需要无穷多的涂料;然而把涂料倒进Gabriel喇叭填满整个内部空间,所需要的涂料反而是有限的。
有网友一定会问,那有没有什么二维图形,面积有限大,周长却无限长呢?答案是肯定的,Koch雪花就是这样一个经典的例子。不过,通过分形构造出来的这类图形似乎并不存在涂料悖论,因为递归到一定深度时分形图形的尺度将小于表面涂料的厚度,因此表面大小不能永无止境地算下去,涂满表面所需的涂料不再是无穷多。当考虑到涂料厚度时,原先的悖论也可以解释清楚了:填充内部空间仅仅涂满了图形的内表面,一旦考虑到涂料的厚度,它和外表面的区别就出来了。
最酷的证明:Pick定理另类证法
难以想像,一段小小的证明竟然能比一个瘦小的留着长头发穿黑色短袖T恤紧身牛仔裤边跳边弹吉他的MM还要酷。原来一直以为这个证明已经很酷了,现在显然我已经找到了一个更酷的证明。
Pick定理是说,假设平面上有一个顶点全在格点上的多边形P,那么其面积S(P)应该等于i+b/2-1,其中i为多边形内部所含的格点数,b是多边形边界上的格点数。绝大多数证明都是用割补的办法重新拼拆多边形。这里,我们来看一个另类的证明。
假设整个平面是一个无穷大的铁板;在0时间,每个格点上都有一个单位的热量。经过无穷长时间的传导后,最终这些热量将以单位密度均匀地分布在整个铁板上。下面我们试着求多边形P内的热量。考虑多边形的每一条线段e:它的两个端点均在格点上,因此线段e的中点是整个平面格点的对称中心,因而流经该线段的热量收支平衡(这半边进来了多少那半边就出去了多少),即出入该线段的热量总和实际为0。我们立即看到,P的热量其实完全来自于它自身内部的i个格点(的全部热量),以及边界上的b个格点(各自在某一角度范围内传出的热量)。边界上的b个点形成了一个内角和为(b-2)*180的b边形,从这b个点流入P的热量为(b-2)*180/360 = (b-2)/2 = b/2-1。在再加上i个内部格点,于是S(P)=i+b/2-1。
来源:
http://zhuhcheng.spaces.live.com/blog/cns!DE38E96268C49F28!212.entry
http://www.math.ethz.ch/~blatter/Pick.pdf
趣题:2n+1个点中任n个都与同一点相连,则存在一个连接所有点的点
有2n+1个人,他们的朋友关系满足这样一种奇特的性质:任选n个人,则在剩下的人中总能找到一个人,他和这n个人都是朋友。求证,存在这样一个人,他和所有人都是朋友。我们假设朋友关系是双向的,也就是说如果A是B的朋友,那么B一定是A的朋友。
这明显可以转化为一个图论问题。选出两个互为朋友的人。我们得到了一个大小为2的团(一个“团”就是一个所有结点两两相连的子图,或者干脆说是完全图形状的子图)。和另外n-2个人并在一起,则存在一个人和他们都是朋友(当然和那两个人也就是朋友了)。把这个人加进刚才那个团里,于是我们得到了一个大小为3的团。又随便取n-3个人和这3个并在一起,则有一个人和所有这些人都是朋友,于是我们继续扩展出一个大小为4的团。反复进行这个操作,直到我们得到一个大小为n+1的团,此时团的大小已经不能再继续扩展了。但是,一旦注意到此时不属于团的人只剩n个了时,我们发现问题已经解决了:在团里面存在一个人P,他和不属于这个团的那n个人都是朋友。而P本身在一个大小为n+1的团里面,他和团里的其余n个人都是朋友。因此,P和所有人都是朋友。
来源:http://www.cut-the-knot.org/arithmetic/combinatorics/Clique.shtml
趣题:循环赛中总存在一人“可传递一次”地打败了所有人
n个人中每两个人之间都进行过一次比赛。假设比赛不可能出现平局。证明,一定能找出这样的一个人,对于其它任何一人p,他击败了p或者击败了某个打败了p的人。
一句话证明:赢的次数最多的那个人显然满足我们的条件。反证,假设被他打败的所有人的集合为P,万一有个人既没有输给他,也没有输给P里面的任何一人,那这个人至少赢了|P|+1次,成了获胜次数更多的人,矛盾。我故意在这里多写一句话,目的是想说明前面的空白有多短。在Ctrl+A之前,不妨试试看自己能否想到如此简单的证明。
来源:http://www.cut-the-knot.org/arithmetic/combinatorics/RoundRobinTournament.shtml