三个好朋友到一家餐厅吃饭。饭快吃完的时候,一个服务员过来告诉他们说,他们的账单已被匿名支付了。三个人都尊重他人匿名付款的权利,但同时他们也想知道,这个匿名支付者是他们三位中的一个,还是他们三人之外的一个第四者。有没有什么办法能够让他们知道在他们之间是否有人付账,但又保证任何人都推测不出究竟是谁付的账?利用三枚硬币可以轻易做到这一点。你能想到这个办法吗?
证明
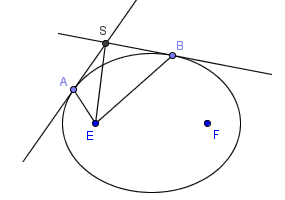
趣题:椭圆焦点到两切线交点的连线平分焦点对两切点的张角
八卦的学问:实现所有人消息共享最少需要多少通电话?
最近看到了一个有趣的问题Gossip Problem。假如我们班有n个MM,每一个MM都有一个独家八卦消息。两个MM可以通过电话联系,一通电话将使得双方都获知到对方目前已知的全部消息。要想所有n个MM都知道所有n条八卦消息,最少需要多少通电话?
一个最简单的办法就是从n个人中选一个消息汇总人,所有n-1个人都打电话给她,她再打电话给所有人。这样总共需要2n-2通电话。其实,汇总阶段的最后一通电话和发布阶段的第一通电话可以合并为一通电话,这样的话该方案实际上只需要2n-3通电话。打电话的次数还能更少吗?给出一个最优解,并证明这个数目已经不能再少了。
显然,n=2时只需要一通电话,n=3时必须要3通电话。当n=4时,可以让AB互相通话,CD互相通话,此时每个人都知道了(包括自己的)两条消息;然后A和C通话,B和D通话,从而使得每个人都获知另外两条自己还不知道的消息。显然,对于4个人的情况,4通电话已经是最少的了。
对于n>4的情况,有一种算法可以保证在2n-4通电话内解决问题。首先,选出4个人作为消息汇总人。其余每个人都选择一个汇总人并与之通话;然后4个汇总人再用4通电话互相更新一下消息(用刚才n=4的办法);最后4个汇总人把电话再打回去,实现所有消息全部共享。下面我们证明,2n-4已经是最少的了。证明方法很多,也都很复杂。最常见的证明由Brenda Baker和Robert Shostak在1972年给出。
经典证明:不用数学归纳法直接推导平面图的Euler公式
把《三体II黑暗森林》看完后,又把上学期已经放下的Proofs from THE BOOK拿出来翻了几页。当结束了数论部分进入几何学时,一些离散性的东西让整本书陡然科学了起来。前面那篇日志里的牛B证明就是我从这本书的第9章中看到的,运用线性代数的基本定理我们居然可以证明一个无从下手的图论问题!今天我又看到牛B证明了:平面图Euler公式V+F=E+2的非数学归纳法证明。以前我见到过各种Euler公式的证明,证明方法千奇百怪,其中不乏很多独具匠心的精巧证明,但它们本质上都是运用数学归纳法不断拆边重组减低规模,将复杂的平面图一点一点变得简单。在Proofs from THE BOOK的第11章,我见到了一个用半页纸写下的巧妙证明,证明方法简单、美观而有趣,读后让人会心一笑。

在介绍这个证明之前,让我们先来回顾一下什么是Euler公式。Euler公式是说,在一个由若干顶点和它们之间的一些不相交的边所组成的图中,等式V+F=E+2总成立,其中V表示顶点个数,E表示总的边数,F表示这个图分割出来的区域个数(包括一个“外部区域”,例如一个圆把平面分割为两个区域)。如图1,这个图共有6个顶点、10条边和6个区域,可以看到6+6=10+2是成立的。为了证明这个结论,考虑这个图的任意一个生成树(图1中加粗了的边)。再考虑这个图的“对偶图”:新图的每个顶点代表原图的一个区域,原图的两个区域相邻则在新图上的两个对应顶点之间连一条边(图2中的虚线部分)。接下来,我们找出原图中那些不属于生成树的边界线,把它们在新图中所对应的边加粗(图2中的加粗虚线)。容易看出,加粗的虚线是连通的,因为原图的粗线条是一棵生成树,它没有隔离出任何一块区域;同时呢,加粗虚线是没有环的,否则它将把某个原图的顶点包起来,从而原图中的加粗线条就不可能是生成树了。只需要注意到一棵树的顶点数等于边数加一,我们的结论就直接出来了:原图的顶点数就是Euler公式中的V,它等于原图生成树的边数加一;新图的顶点数就是Euler公式中的F,它等于新生成树的边数加一;而两棵生成树的边数总和正好就是原图中的E。于是呢,我们就得到了V+F=E+2。
趣题:完全图K_n最少可以拆成多少个完全二分图?
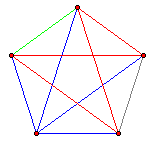
一个完全图K_n是指一个有n个顶点的图,其中每两个点之间都有一条边相连。一个完全二分图是指这样一种图,图中的顶点分为两个点集L和R,L里的每个顶点都和R里的所有点相连。上图显示了一种把K_5划分为四个完全二分图的方法(分别用红蓝绿灰四种颜色来表示这四个子图)。你觉得,最少可以把完全图K_n划分成多少个完全二分图?给出一种划分方案,并证明这个数目已经不能再少了。