如果删除字符串A中的若干字母可以得到字符串B,我们就说A包含B(熟悉相关概念的网友可能知道,有一个准确的说法叫做“B是A的子序列”,但为了避免和后面的“序列”混淆,我们不用这种说法)。例如,字符串“matrix”包含了“mix”,也包含“ati”,但不包含“it”。字符串序列aaaaa, ab, bbaa, baaaa, aa, bbacc, cbcacc, bb中的每个字符串都不包含它前面的任何一个字符串,我们称这样的字符串序列为“非生成序列”(我自己取的名字,意思是说任一字符串都不能由前面的项通过添加字母生成出来)。我们可以构造出任意长的非生成序列,例如字符串长度严格递减的序列,或者所有不同的长度为n的字符串。现在的问题是,你能构造出一个无穷长的非生成序列吗?当然,你不能使用无穷多种字母来达到这一点。
证明
经典证明:Chaitin定理 不可能编程判断代码的最简性
今天学到一个好玩的东西。仿照停机问题的研究方法,我们可以想出很多有趣的不可解问题。Gregory Chaitin曾经提出过下面这个问题。如果两段代码运行之后能够输出相同的结果,我们就称较短的代码比长一点的那个更简洁(注意,如果程序需要读入数据,读入的数据也算进代码长度)。对于一个指定的输出,一定存在一个“最简的”代码,它是所有能输出此内容的程序代码中最短的一个。在刚刚结束的TLE比赛中,参数选手拼了命地缩减每一个字符,写出来的代码一个比一个短。有人或许在想,这些代码究竟能短到什么程度?你如何才能知道你的代码已经不再有改进的空间了?受此启发,我们的问题出来了:你能否编写一个程序,使得该程序能够判断任意一段代码是否是最简的?
Chaitin定理指出,上述问题是一个不可解问题,再牛的人也不可能编写出这样的程序。证明方式与大多数此类问题一样,都是采用反证加构造的方法证明的。你能想到这个证明方法吗?
关于0.9999….=1的证明
某日凌晨4点多,网友Superwyh发来短信说,他梦到了这样一个颇具启发性的问题:如果我们能够证明两个数之间不存在其它的数,这是否足以说明这两个数是相等的?正好当时我还没睡,稍微想了一下,发现这个命题是成立的,因为它的逆否命题显然成立。倘若两个数不相等,那它们之间一定能够插入其它的数(例如这两个数的算术平均值);反过来,如果两个数之间无法插入别的数,这两个数自然就应该相等了。
这个命题是相当具有启发性的。或许有人会想,能不能用这一思路去证明两个数相等呢?
关于两数是否相等的争论,最著名的就是那个关于0.9999….和1是否相等的问题了。这一问题理解起来简单,细想起来争议颇大,真可谓是一个全民化的数学争论,与著名的Monty Hall问题有得一拼。不了解极限概念的人可能会说,不管你在后面写多少个9,它都不能达到1的,量变和质变存在本质上的区别。因此,当高中数学课上老师明确指出0.9999….精确地等于1时,还是有不少人瞠目结舌,甚至高声反对。
一个难看的证明和一个漂亮的证明
正逢考试周,抱歉这几天更新很慢。最近6天天天都有考试,今天上午考完英语后,终于有机会喘一口气了。下一次考试是后天下午的古代文学史,打算从明天开始借别人的笔记来背。今天下午先稍微休息一下。
前几天准备考离散数学时,烦躁得真想把课本撕了。北大出的那本《离散数学教程》是我所见过的最破的教材,里面频繁出现一些诸如假设m和n怎么怎么样结果推出了p和q怎么怎么样的印刷错误;在短短三页纸中,“Peano”被拼写错了四次,而且每次错的都不一样。
离散数学本身是相当科学的。离散数学中的证明,特别是图论证明,都是相当有趣的。但是,课本上的证明写得太丑了,符号和语言晦涩难懂,思维缺乏直观性和启发性。于是呢,我深刻体会到了这个Blog存在的必要性。我非常反对缺乏直观思维方式的证明过程。一个合格的教科书需要在严格的形式证明之外附上一段证明思路的直观描述。大家或许注意到了,我在写Blog时很不愿意定义变量,能用自然语言描述的地方就尽可能用自然语言来说。在介绍种种精妙的趣题和证明时,我往往会改变证明步骤的顺序和语言表述的方式,以顺应人的直观思维方式;否则,证明的巧妙性和启发性很难被表现出来。
根号2是无理数的又一个精彩证明
The American Mathematical Monthly新年第一期中有一段精彩的根号2无理性证明。
假设√2等于p/q,那么对于任意自然数n都有:
(√2)n q = 2n/2 q 当n是偶数时
2(n-1)/2 p 当n是奇数时
无论哪种情况,(√2)n q都是一个自然数。由二项式定理,对任意大的n都有:
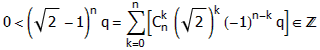
但这显然是不可能的,因为序列(√2 – 1)n q是收敛到0的。
参考资料:http://www.cut-the-knot.org/proofs/sq_root.shtml#proof16
相关文章:五种方法证明根号2是无理数,又一种证明根号2是无理数的方法