勾股定理有上百种证明，但其实它们都大同小异——无非是构造一组三角形和正方形并进行一系列变换。今天我看到了一个用圆面积来解释勾股定理的办法，颇有一些新意。
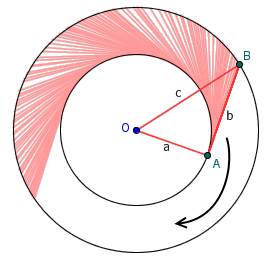
考虑直角三角形OAB绕着一个锐角顶点O旋转一周。顶点A的轨迹是一个半径为a的圆，顶点B的轨迹是一个半径为c的圆。那么，线段AB扫过的区域（一个圆环）的面积就应该是大圆面积减去小圆面积，即π(c^2-a^2)。如果我们能够有一种办法说明，线段AB扫过的面积正好是πb^2，我们就相当于得到了勾股定理的另一个证明。
证明
俄罗斯方块可以永无止境地玩下去吗？
大家在玩俄罗斯方块的时候有没有想过这样一个问题：如果玩家足够牛B的话，是不是永远也不可能玩死？换句话说，假设你是万恶的游戏机，你打算害死你面前的玩家；你知道任意时刻游戏的状态，并可以有针对性地给出一些明显不合适的方块，尽量迫使玩家面对最坏情况。那么，你有没有一种算法能保证害死玩家，或者玩家无论如何都存在一种必胜策略呢？注意，俄罗斯方块的游戏区域是一个宽为10，高为20的矩形，并且玩家可以预先看到下一个给出的方块是什么。在设计策略时，你必需考虑到这一点。
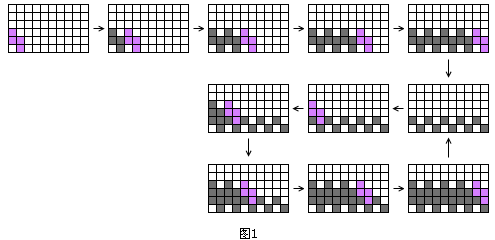
相信很多人有过这样的经历：玩俄罗斯方块时一开局就给你一个“S”型方块，让完美主义者感到异常别扭；结果，第二个方块还是这个“S”，第三个方块依旧是“S”，相当令人崩溃。于是，我们开始猜测，如果游戏机给你无穷个“S”形方块，玩家是不是就没有解了？答案是否定的。如图1，从第10步开始，整个局面产生一个循环；只要机器给的一直都是“S”方块，玩家可以不断重复这几个步骤，保证永远也死不了。
不过，这个循环是在游戏场地清空了的情况下才产生的。有人会进一步想了，要是在玩着玩着，看着你局势不好时突然给你无穷多个“S”方块呢？事实上，此时局面的循环依然可能存在，如图2。在第5个“S”形方块落地后，循环再次产生。
有限域的二次剩余与x^2+y^2=c的解的个数
上个月的UyHiP谜题涉及到一些抽象代数的东西：考虑一个有f个元素的有限域，其中c是有限域中的一个元素。试求x^2+y^2=c有多少个解。你的答案应该是一个关于f和c的函数。
有趣的是，对所有c≠0的情况，x^2+y^2=c的解的个数与c都是无关的。事实上，方程解的个数只与f模4的余数和c是否为零元有关。具体地说：
| c = 0 | c ≠ 0 | |
| f mod 4 = 0 或 2 | f | f |
| f mod 4 = 1 | 2f – 1 | f – 1 |
| f mod 4 = 3 | 1 | f + 1 |
经典证明：推箱子游戏所需步数可达指数级
今天在写一个稿件时又翻阅了一下Erich Friedman的Math Magic，发现了一个有趣的东西——场地大小为n的推箱子游戏所需要的最少步数最坏情况是多少。下面这个构造说明，最坏情况至少也是指数级的。
首先，让我们来看看该构造中的一个基本单元：
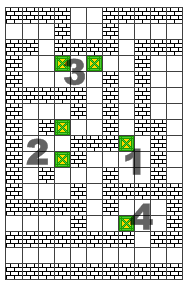
这个构造中共有6个箱子，且它们都已经在目的位置上了。不难看出：
1. 假如你人在这个区域之外，你只可能从右上角的出入口进入该区域，从其它地方进去都会导致死局
2. 从右上角进入后你只能往下走，进入1区；走左边的话直接导致死局
3. 你可以通过2区前往3区，但若从3区左上角的出口出去了，则2区动过的箱子将永远无法回到原位（除非你原路返回）
4. 你可以通过2区前往3区，并把3区左边的那个箱子左移一格，再返回2区；这样下次你再从右上角进入该区域时便可以直接经过3区从左上角出去
5. 最后你只能从4区离开
一个实际问题：如何放本本使得其占地面积最小？
我的书桌已经乱到一定的程度了，以至于每次把笔记本从包包里拿出来，准备把它放到桌子上去时，我都要在桌子上非常下功夫地寻找一块能够放得下本本的空地。久而久之，我开始思考：怎样放置笔记本才能使得它占据桌面的面积最小，而又保证它不会掉下去呢？