说勾股定理是一切科学的基础恐怕一点也不夸张。一些最基本的物理定律就与勾股定理之间产生了完美的对应。在我初三学到动能的公式时,我就想到,动能与速度的平方成正比是有内在原因的,这正是由数理科学中最基本的定理——勾股定理——决定的。考虑一个质量为1的物体向正北方向运动,如果它的速度为a,那么所需要的能量就是(a^2)/2;类似地,让同一个物体以b的速度向正东方向运动,所需要的能量应该为(b^2)/2。如果把这两个力叠加在一起,我们就得到了这样一个事实:用(a^2)/2 + (b^2)/2的能量可以让物体往大致东北的方向运动,其速度正好就是一个以a和b为边的矩形的对角线长。因此,(a^2)/2 + (b^2)/2正好也就是对角线长度的平方的一半,这恰好与勾股定理的内容一致。可以说,我们用数学定理验证了一个物理定律;也可以说,我们用物理定律证明了一个数学定理。
证明
Pick定理的几个出人意料的应用
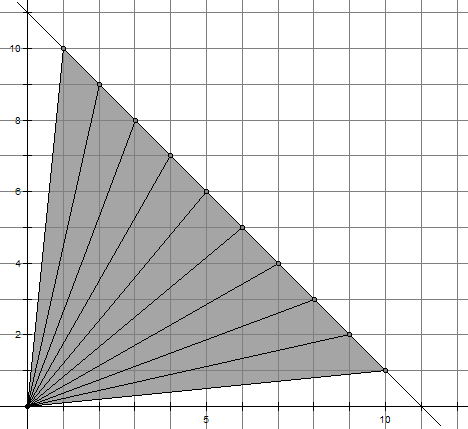
考虑直线x+y=n,其中n是一个素数。这条直线将恰好通过第一象限里的n-1个格点(如上图,图中所示的是n=11的情况)。将这n-1个点分别和原点相连,于是得到了n-2个灰色的三角形。仔细数数每个三角形内部的格点数,你会发现一个惊人的事实:每个三角形内部所含的格点数都是一样多。这是为什么呢?
趣题:用松了的圆规作给定一端点的指定长度线段
《几何原本》的命题1是“作以给定线段为边的等边三角形”,其做法也正如大家所料:以AB为半径,分别以A、B为圆心作圆,交点C就是等边三角形的第三个顶点,于是连接AC和BC即可。《几何原本》的命题2则是一个看似更加简单的作图问题:给定点A和线段BC,作以A为其中一个端点的、长度等于BC的线段。我原以为《几何原本》的做法也和我们平常的做法一样——以A为端点向任意方向作一射线,再用圆规截取出和BC等长的线段。因此,每次在网上看到关于《几何原本》命题2时,我都会直接略过去。最近我才发现,《几何原本》中命题2的做法和大家想象的完全不一样,因为这种做法在《几何原本》中是不允许的。圆规只能用来作圆,不能用来度量和转移长度;换句话说,公设3中的“圆规”是一个“松”的圆规,一旦离开纸面后圆规的两脚便会“啪”的一声自动合拢。在这种条件下,你又如何实现上面提到的作图问题呢?
证明集合可数的简便方法
在集合论中,一个重要的概念就是集合的可数性。我们说一个集合是可数的,如果这个集合内的元素能够与自然数集N建立一一对应的关系。换句话说,我们能够给这个集合里的所有元素按次序排好,能够以某种顺序为所有元素进行编号。在这里,我们看到了两个重要的结论:全体有理数集合是可数的,以及全体实数集合是不可数的。在证明全体有理数可数时,我们用到的方法通常是当年Cantor所用的对角线方法。不过,事实上我们还有一个更简便的方法。在证明一个集合可数时,我们只需要建立一个映射到自然数集N的函数,使得每个自然数的原像都只有有限个即可。这样的话,我们便可以从小到大考虑自然数集中的每个元素,列举出它所对应的原像,从而得到原集合的一种编号次序。
例如,欲证明全体整数是可数的,只需要考虑函数f(x)=|x|,这是一个从全体整数到自然数的函数,并且每个自然数最多只有两个原像。这样的话,我们便可以立即说明全体整数是可数的。类似地,为了说明全体有理数也是可数的,只需要令函数f(p/q)=|p|+|q|。显然分子分母的绝对值和为某一指定自然数的只有有限多种情况。
趣题:随机选取两个无穷大的图,求两者相同的概率
假设我们俩各自独立地随机选取一个有无穷多个顶点的图(两点之间1/2的概率有边1/2的概率没有边)。那么,我们俩选到相同的图的概率是多少?
令人难以置信、但想通了之后又异常显然的是,两个图相同的概率为1。并且,我可以精确地告诉你,这个相同的图是什么样子的。考虑这样一个无穷大的图,我们用自然数1, 2, 3, …给所有顶点标号,然后如果y的二进制表达中的右起第x位为1,就在顶点x和顶点y之间连一条线。比如,顶点5就和顶点1、顶点3相连。我可以证明,我们俩都100%地会选取到上述这个图。