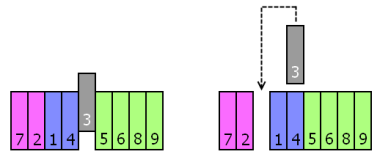
书架的某一层里放了一套百科全书，但它们排列的顺序却是乱的。一个傻子想要把这套书排好顺序，也就是说他想要书架里的书从左至右分别是第 1 卷，第 2 卷，……，第 n 卷。他给这套书排序的办法是这样的：不断取出一本原应放在更左边的书，插进它该在的位置。比方说，某本书的卷号是 3 ，它的位置却是左起第 5 ，位于其目标位置的右侧。那么傻子就可以把这本书拿出来，插入当前左起第 2 本书的右边，把那些占了它位置的书挤到更右边去，而不管这一操作是否会破坏掉已经就位的书。注意到这种排序法很可能捡了芝麻，丢了西瓜，为了一本书的位置而破坏掉一连串原已排好的书，可谓是鼠目寸光，缺乏远见。我们的问题是，在哪些情况下这样的排序法最终一定能实现排序，哪些情况下可能会陷入永无止境的死循环？
在继续探索多边形内接图形问题之前，我们先来看一个看似无关的趣题。从水平线上的一点起笔，在这条水平线上方随意画一条折线段，最后回到水平线上（如下图）。把这个折线段想象成一座座山峰。我们以最高峰所在位置为界把整座山分成左右两部分。现在，假设有一对相恋的登山者，一个站在最左侧的山脚出（即点 0 处），一个站在最右侧山脚处（即点 0′ 处）。这两个人将同时从山脚出发，同时到达山顶，并且保证在此过程中他们俩总处于同一海拔高度。不管这座山是什么形状，这种浪漫的想法总可以实现吗？
注意，在登山的过程中，登山者可以为了照顾对方而走回头路。例如，对于图中所示的小山，两个人可以按照下列方法实现同步登山。左右两个人的路线分别为：
0 → 1 → 2 → 3 → 4 → 5 → 6 → 5 → 4 → 3 → 2 → 1 → 2 → 3 → 4 → 5 → 6 → 7
0'→ 1'→ 2'→ 3'→ 2'→ 3'→ 4'→ 5'→ 6'→ 5'→ 6'→ 7'→ 8'→ 9'→ 8'→ 9'→ 10'→ 11'
当我们进一步考虑内接菱形时，情况有了一些变化——证明任意多边形内均存在内接菱形没有前几个问题那么容易了。但我们可以轻易证明一个弱化版的命题：任意凸多边形内均存在内接菱形。下面将给出这个命题的两种不同的证明，它们都相当经典。
证明 1 ：考虑凸多边形内的一条水平线段由上至下扫过，这条线段的中点所形成的轨迹就是一条连接凸多边形最顶端与最底端的折线段。类似地，考虑一条从左至右移动的竖直线段，它的中点就构成了从凸多边形最左端到最右端的连线。显然，这两条连线会有一个交点，也就是说我们找到了两条互相垂直且中点重合的线段，它们对应的四个端点显然就是一个菱形的四个顶点。
大家或许知道 Banach-Tarski 悖论——把一个三维球分成有限多份并重新拼成两个和原来一模一样大的球——这个悖论告诉我们利用选择公理我们能够推出看上去多么不合逻辑的东西。今天我听说了另一个类似的悖论叫做 Sierpinski-Mazurkiewicz 悖论，它的结论在直观上同样令人难以接受，并且推导不依赖于选择公理。
Sierpinski-Mazurkiewicz 悖论是说，存在平面上的一个点集 S ，我们能把它划分成两个子集 A 和 B ，使得 A 旋转 1 弧度后与 S 完全重合， B 平移一个单位后也与 S 完全相同。换句话说，存在这么一个点集，我们能把它分成两个与自身一模一样的子集！这听上去实在是不可思议，然而构造却极其简单。
紧接着，我们想问：是否任意一个多边形内都能找到内接矩形呢？有意思的是，答案也是肯定的。但此时，前一节我们用到的两种证明方法现在都派不上用场了，我们需要用到一些全新的手段。下面这个证明真可谓是巧妙到了诡异的地步，真不知是谁想出来的。
对于多边形边界上的任意两点 A(x1, y1) 、 B(x2, y2) ，作出它们在三维空间中所对应的点 ((x1+x2)/2, (y1+y2)/2, √(x1-x2)^2+(y1-y2)^2) 。换句话说，把多边形放在水平面 z=0 上，对于多边形上的每一组无序点对 A 、 B ，在线段 AB 中点的正上方 |AB| 处作一个点。再把这个多边形本身加进去，我们就得到了一个三维空间中的封闭曲面。
可以看到，图中所示的例子中，这个曲面与自身相交了。这就表明，存在多边形边界上的两组点对 A 、 B 和 C 、 D ，它们满足线段 AB 和 CD 的中点重合，并且两线段一样长。这样，四边形 ABCD 就是多边形的一个内接矩形了。下面我们将说明，这个曲面一定会与自身相交。