上个月的 UyHiP 趣题非常妙,个人认为是近几个月里最漂亮的一道谜题了。
典狱长要和 100 个囚犯玩这么一个游戏。典狱长给每个囚犯发两个手套,一个黑色的,一个白色的。之后,每个囚犯的额头上都会写上一个实数,所有这 100 个实数互不相同。每个囚犯都能看到其他 99 个囚犯前额上所写的数,但不能看到自己的数。接下来,每个囚犯必须独立地决定把哪个手套戴在哪只手上。等到所有囚犯都戴好了手套,典狱长会把他们按照前额上所写的数从小到大地排好,并要求他们手牵着手站成一横排。如果每两只握在一起的手都戴着相同颜色的手套,那么所有 100 个囚犯都可以被释放。
在游戏开始前,他们可以聚在一起,商量一个对策。游戏开始后,囚犯与囚犯之间不允许有任何交流。囚犯们能够保证全部释放吗?
证明
谬证大全:1+1≠2的n种可能
最近看到几个有趣的数学谬证,想写下来与大家分享;结果写到这个又想到那个,一写就写个没完,于是想到干脆做一篇谬证大全,收集各种荒谬的证明。
如果你有什么更棒的“证明”,欢迎来信与我分享,我会更新到这篇日志中。我的邮箱是 matrix67 at tom.com ,或者 gs.matrix67 at gmail.com 。
1=2?史上最经典的“证明”
设 a = b ,则 a·b = a^2 ,等号两边同时减去 b^2 就有 a·b – b^2 = a^2 – b^2 。注意,这个等式的左边可以提出一个 b ,右边是一个平方差,于是有 b·(a – b) = (a + b)(a – b) 。约掉 (a – b) 有 b = a + b 。然而 a = b ,因此 b = b + b ,也即 b = 2b 。约掉 b ,得 1 = 2 。
这可能是有史以来最经典的谬证了。 Ted Chiang 在他的短篇科幻小说 Division by Zero 中写到:
There is a well-known “proof” that demonstrates that one equals two. It begins with some definitions: “Let a = 1; let b = 1.” It ends with the conclusion “a = 2a,” that is, one equals two. Hidden inconspicuously in the middle is a division by zero, and at that point the proof has stepped off the brink, making all rules null and void. Permitting division by zero allows one to prove not only that one and two are equal, but that any two numbers at all—real or imaginary, rational or irrational—are equal.
这个证明的问题所在想必大家都已经很清楚了:等号两边是不能同时除以 a – b 的,因为我们假设了 a = b ,也就是说 a – b 是等于 0 的。
趣题:半径相等的半圆和圆 内接正方形的面积之比
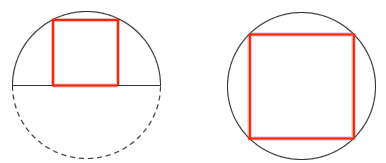
在半径相等的半圆和圆中各画一个内接正方形。这两个正方形的面积之比是多大?有什么简单些的算法吗?
Read more…
用数学解赌博问题不稀奇,用赌博解数学问题才牛B
有一个经典的概率问题:平均需要抛掷多少次硬币,才会首次出现连续的 n 个正面?它的答案是 2^(n+1) – 2 。取 n=2 的话,我们就有这样的结论:平均要抛掷 6 次硬币,才能得到两个连续的正面。或许这个期望次数比你想象中的要多吧。我们不妨试着来验证一下这一结果。由简单的递推可得,所有 1 都不相邻的 k 位 01 串有 Fk+2 个,其中 Fi 表示 Fibonacci 数列中的第 i 项。而“抛掷第 k 次才出现连续两个正面”的意思就是, k 位 01 串的末三位是 011 ,并且前面 k – 3 位中的数字 1 都不相邻。因此,在所有 2^k 个 k 位 01 串中,只有 Fk-1 个是满足要求的。因此,我们要求的期望值就等于 ∑ (k=2..∞) k * Fk-1 / 2^k 。这个无穷级数就等于 6 。我怎么算的呢?我用 Mathematica 算的。
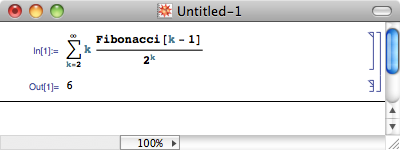
显然,当 n 更大的时候,期望值的计算更加复杂。而简单美妙的结论让我们不由得开始思考,这个问题有没有什么可以避免计算的巧妙思路?万万没有想到的是,在赌博问题的研究中,概率论帮了不少大忙;而这一回,该轮到赌博问题反过来立功了。
Read more…
100个囚犯和灯泡的那些事儿(下)
即使灯泡的初始状态不定,当 n=2 时,两个人也能保证都知道对方进过房间。假设双方手中各有两个球,囚犯 A 总是试图把自己的小球放进盒子,囚犯 B 总是试图把小球取走。如果 B 拿到了 4 个小球,他就知道了 A 一定来过房间;而只要 A 放好的小球被拿走了, A 也知道 B 进过了房间。
但是,当 n>2 时,不存在这样的协议,使得有两个人都能获知所有人都已进过房间。 Peter Winkler 的 Mathematical Puzzles: A Connoisseur’s Collection 一书中给出了这个结论的一个大致证明思路。
让我们考虑其中任何一个囚犯。我们假设他的策略是确定性的,他的下一步行动完全取决于之前看到的状态序列。假设在某一步,他看到的状态和上次离开房间时的状态相同,但他选择了改变状态。这时,你可以质问他,那你为啥不在上次就把状态改过来,偏偏要这次才去扳开关呢?看守完全有可能连续两次都是叫你进的房间,这样你不就浪费了一次进房间的机会了吗?因此,我们可以假设,当他进入房间时看见的状态和上次走的时候一样,他是不会去扳动开关的。
接下来,让我们假设在某一步,这个囚犯的策略是“不动开关,保留原状态”。那么,我们可以认为他以后就再也不会动那个开关了!因为在最坏情况下,他根本没有改变灯泡状态的机会!具体地说,若无视掉这个囚犯以后的行动,今后的房间状态序列里必然有一种状态将出现无穷多次,比方说状态“开”出现了无穷多次吧。那么在最坏的情况下,这个囚犯从此开始总是在开灯的时候进屋。而他在这一步没有变动开关,并且以后的每一步里他所看到的状态都将和上次看到的一样,因此以后他都不会变动开关了。