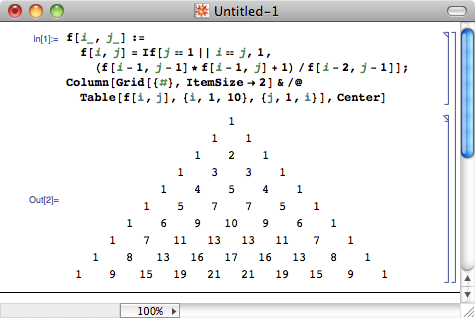
如果有人问你，三角形
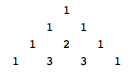
的下一行数是什么，你一定会毫不犹豫地说，下一行是 “1 4 6 4 1” ——这是 Pascal 三角，每个数都等于两肩的数之和。不过，最近 The College Mathematics Journal 上的一篇论文却给出了一个同样合理的正确答案： 1 4 5 4 1 。理由同样对称而美观：每个数都等于两肩的数之积加 1 ，除以头顶上（再上一行的对应位置上）的数。例如，第 2 个数 4 就等于 (1*3 + 1) / 1 ，而第 3 个数 5 则等于 (3*3 + 1) / 2 。我们不妨就紧跟 Pascal 的脚步，把它取名为 Rascal 三角吧。
有网友肯定会说了，你就瞎掰吧， Rascal 三角形的生成规则里有除法，这会让三角形里面充斥着大量的分数的。你错了，这才是 Rascal 三角形的神奇之处：尽管每个数都是由两数相除得来的，但它们保证都是整数！你能看出这是为什么吗？
大家或许都知道经典的两人分饼问题——为了实现公平性，只需要一个人切，另一个人选即可。不过，在现实生活中，情况远没有那么理想。如果把大饼换成蛋糕，问题就复杂了很多——你想吃奶油，我想吃巧克力，他想吃水果⋯⋯如果分蛋糕的人对蛋糕各部分的价值看法有分歧，还能实现公平的分割吗？如果分蛋糕的人不止两个呢？
事实上，对于两个人分蛋糕的情况，经典的“你来分我来选”的方法仍然是非常有效的，即使双方对蛋糕价值的计算方法不一致也没关系。首先，由其中一人执刀，把蛋糕切分成两块；然后，另一个人选出他自己更想要的那块，剩下的那块就留给第一个人。由于分蛋糕的人事先不知道选蛋糕的人会选择哪一块，为了保证自己的利益，他必须（按照自己的标准）把蛋糕分成均等的两块。这样，不管对方选择了哪一块，他都能保证自己总可以得到蛋糕总价值的 1/2 。
不过，细究起来，这种方法也不是完全公平的。对于分蛋糕的人来说，两块蛋糕的价值均等，但对于选蛋糕的人来说，两块蛋糕的价值差异可能很大。因此，选蛋糕的人往往能获得大于 1/2 的价值。一个简单的例子就是，蛋糕表面是一半草莓一半巧克力的。分蛋糕的人只对蛋糕体积感兴趣，于是把草莓的部分分成一块，把巧克力的部分分成一块；但他不知道，选蛋糕的人更偏爱巧克力一些。因此，选蛋糕的人可以得到的价值超过蛋糕总价值的一半，而分蛋糕的人只能恰好获得一半的价值。而事实上，更公平一些的做法是，前一个人得到所有草莓部分和一小块巧克力部分，后面那个人则分得剩下的巧克力部分。这样便能确保两个人都可以得到一半多一点的价值。
但是，要想实现上面所说的理想分割，双方需要完全公开自己的信息，并且要能够充分信任对方。然而，在现实生活中，这是很难做到的。考虑到分蛋糕的双方尔虞我诈的可能性，实现绝对公平几乎是不可能完成的任务。因此，我们只能退而求其次，给“公平”下一个大家普遍能接受的定义。在公平分割 (fair division) 问题中，有一个最为根本的公平原则叫做“均衡分割” (proportional division) 。它的意思就是， 如果有 n 个人分蛋糕，则每个人都认为自己得到了整个蛋糕至少 1/n 的价值 。从这个角度来说，“你来分我来选”的方案是公平的——在信息不对称的场合中，获得总价值的一半已经是很让人满意的结果了。
考虑这么一个游戏：不断在区间 [0, 1] 中概率均等地选取随机数，直到所取的数第一次比上一个数小。那么，平均需要抽取多少个随机数，才会出现这样的情况？
答案：记 Pi 为第 i 次才取到小于前一个数的数的概率。则我们要求的就是 P1 + 2 * P2 + 3 * P3 + 4 * P4 + … 。妙就妙在下面这个变形（在继续看下去之前你能想到吗）：
目前，我正在《新知客》杂志上主持一个趣题栏目。每月杂志发行后，我将在 Blog 上同步更新。点击 这里 可以查看往期题目。
推理
1. 高三 (17) 班有 50 个同学，他们的学号分别是 1, 2, 3, …, 50 。一次数学考试结束后，同学们都交完试卷离开了考场。数学老师小 A 清点试卷时发现，他手中只有 49 张卷子。究竟是谁没有交卷呢？正巧小 A 手边没有笔，他也不想把所有卷子按照学号重新排序。他希望不借助任何工具，仅仅通过依次查看每张卷子上写的学号，便能找出缺失的那个学号。和常人一样，小 A 的记忆力很有限，他没法记住之前到底看到过哪些学号；不过，作为一个数学老师，小 A 拥有无人匹敌的计算能力。他有办法找出没交卷的那位同学的学号吗？
2. 小 A 和小 B 玩游戏。从小 A 开始，两个人轮流从 1 到 9 当中选一个数（已经选过的数不能再选），约定谁先选到三个和为 15 的数，谁就获胜了。比方说，小 A 先选了 4 ，然后小 B 选 5 ，小 A 选 6 ，小 B 选 2 。为了阻止小 B 获胜，下一步小 A 就必须得选 8 （否则小 B 将靠 5 、 2 、 8 三个数获胜）。为了阻止小 A 获胜，小 B 选择了 1 （否则小 A 将靠 6 、 8 、 1 三个数获胜）。但是，这已经阻止不了小 A 的胜利了——小 A 可以选择 3 ，从而得到 4 、 8 、 3 三个加起来等于 15 的数。
在这个游戏中，小 A 有必胜策略吗？
