MIT每年一月份都会举行一次谜题比赛(MIT Mystery Hunt)，由上一年的获胜队伍来组织，比赛通常持续两天两夜。每年MIT的解谜比赛都会吸引数千人的到来，他们组成大大小小的队伍，共同参与到解谜游戏中来。游戏要求每支参赛队伍解决近百个谜题，而这些题目的答案又组成了新的谜题(Metapuzzle)；所有这些谜题的答案最终会领引参赛队伍寻找到隐藏在校园中的一块硬币。这些题目不是一般的BT，很多题目连个说明都没有，你要是能独立搞出一两个来你就无敌了。
    今年的谜题已经放在了MIT的网上，大家可以到这里去看看：http://www.mit.edu/~puzzle/08/
    绝大多数题目内容都不知所云，你很可能根本看不出这道题需要你干啥；但事实上，每一道谜题都有唯一的答案。你可以点击右上角的Check Answer看到答案。

官方网站：http://www.abstractica.mjkgames.com/
demo版下载：http://www.abstractica.mjkgames.com/download.html (只含100多关)

这个Blog里已经发过很多在线解谜游戏了，但离线的解谜游戏估计大家还是第一次见到。
下面是我做到的一个很有趣的题目。猜猜看答案是什么？看看有没有人猜到。

    将123456789翻一倍，你会发现结果仍然是这9个数字的一个排列：

123456789 x 2 = 246913578

    我们再次将246913578翻倍，发现：

246913578 x 2 = 493827156

    结果依旧使用了每个数字各一次。操，没完了吗？我们继续翻倍：

493827156 x 2 = 987654312

    牛B了，一个很有特点的数987654312，显然每个数字又只用了一次。
    你或许会想，这下到头了吧，再翻倍就成10位数了。不过，请看：

987654312 x 2 = 1975308624

    又使用了每个数字各一次，只不过这一次加上了数字0。再来？

1975308624 x 2 = 3950617248

    恐怖了，又是每个数字各出现一次。
    出现了这么多巧合之后我们开始怀疑，这并不是什么巧合，一定有什么简单的方法可以解释这种现象的。
    但是，下面的事实让这个问题更加复杂了。到了第6次后，虽然仍然是10位数，但偏偏就在这时发生了一次例外：

3950617248 x 2 = 7901234496 <– 第一次出现例外

    于是，我们不得不相信，前面这一切很可能只是一个巧合，它背后并没有什么简单的原理。
    即使有办法解释这种巧合，解释方法可能也很麻烦。寻找一个漂亮的解释是一个有趣的课题。

http://topsecret.quadium32.com/

根据该站点的统计，目前共有5491个人成功进入了第一关，只有224个人完成了最后一关（第10关）。你会是第225个人吗？

呃……如果你连第一关都不知道该咋办的话，可以看看下面的答案（Ctrl+A显示）：
You have to enter "the password" to access Level 1.

接下来就靠大家自己来完成了。

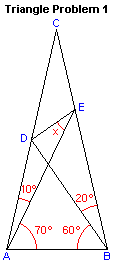    给你四个角度值，请用初等平面几何知识找出x的角度值是多少。这是一道相当难的平面几何题。在这里，这道题被称为是世界上最难的初等几何问题。那个网页上还有这个问题的另一个版本，号称是“世界上第二难的初等几何问题”。引用它的几句话：
    “你只能使用初等几何知识，比如三角形内角和为180度，全等三角形判定法则等等。你不能使用高级的三角学知识，比如正弦定理、余弦定理等等。
    “这是我见过的最难的几何问题。它的确可以用初等几何的方法做出来。这是一个很“正常”的题目，解决它并不需要什么匪夷所思的诡计。
    “抱歉我不会给出这个问题的证明或答案。你只能自己一直做下去，直到问题被成功解决，或者你被这个问题彻底整疯。
    “这个问题有多难？任何一个初中学生都可以读懂证明，但能自己找到证明的人非常非常的少。给我发来电子邮件的几百个人中，估计只有1%到2%的人（多数都是数学教授和大学学生）最终解决了这个问题（没看任何关键的提示）。大多数人以为自己找到了答案，但它们的证明是错误的。
    “这个问题已经在很多地方发表。问题2第一次出现在1922年，问题1第一次出现则是在70年代。我不会告诉你这个问题出自哪里，否则很多人会直接在网上搜答案，而不会去绞尽脑汁地想问题。”

大家动笔挑战吧，我过几天发一份答案。
答案已发布，在这里：http://www.matrix67.com/blog/article.asp?id=431