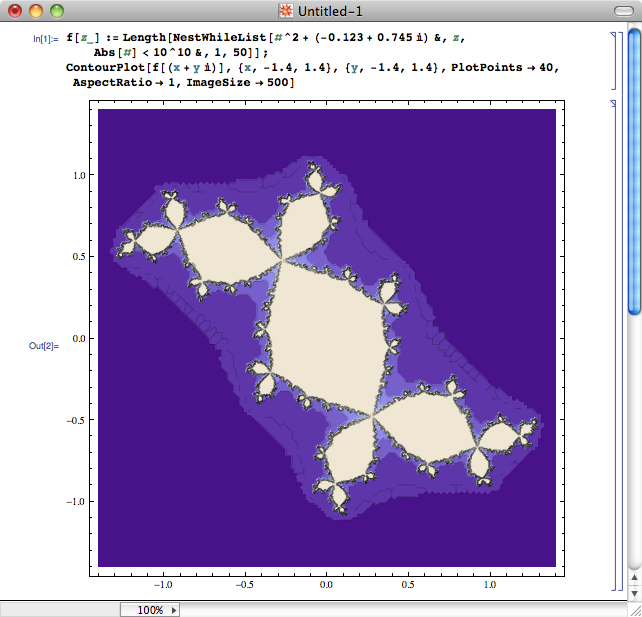
昨天无聊时用 MPlayer 和 Mathematica 做了一张图。大致过程是，用 MPlayer 从各个电影中提取出间隔大致均等的 600 帧图像，导入到 Mathematica 中，再取各帧图像的颜色平均值，用一根根宽度为 1 像素的竖条来表示。得到的结果就是下面这个样子。你能在看到答案之前先猜出电影名字吗？你能识别出每一段颜色都对应着什么情节吗？
Update: 看了大家的回复，我才悲催地发现，这件事情早有人做过了，而且做得比我更好。大家感兴趣的话可以前往： http://moviebarcode.tumblr.com/
很早以前，我简单介绍过 Julia 集和 Mandelbrot 集，文章在此。这可以说是数学中最神秘、最令人敬畏的研究对象之一。不过，那时我对这个话题了解还不太深。今天见到这个网页，让我对 Julia 集和 Mandelbrot 集有了更深的了解。我查阅了一些其他的资料，然后写下这篇长文，与大家一同分享。继续阅读以前，建议先看看我原来那篇文章（很短），那里面有很多漂亮的 Julia 集和 Mandelbrot 集的图片，这篇文章就不再展示了。
还是让我们先来简单复习一下复数吧。由于承认“负数也能开平方”将会带来很多幽雅和便利的结论，因此我们发明了虚数，用 i 来表示 -1 的平方根（即虚数单位），并把实数扩展为复数（即一切形如 a + b i 的数）。正如实数可以用数轴上的点来表示一样，复数可以用平面直角坐标系上的点来表示。令 x 轴表示复数的实数部分，令 y 轴表示复数的虚数部分，则 a + b i 就对应了平面上的点 (a, b) 。我们把这个平面直角坐标系叫做“复平面”。
考虑复数域上的迭代公式 zn+1 = zn^2 + (- 0.123 + 0.745 i) 。取不同的初始值 z0 ，迭代后 zi 的发散速度是不一样的。对于复平面上的每个点，以它为初始值的数列发散速度越快，就染越深的颜色表示；如果以它为初始值数列发散缓慢甚至收敛，则用相对较浅的颜色来表示。那么，整个图形将会是什么样子呢？本人纯手工打造 Mathematica 代码两行，为大家送上这幅神奇的图形：
难以置信，简单的公式竟然生成了如此复杂的分形图形，看上去仿佛是大大小小的兔子竖着耳朵跳出来给大家拜年一样。这个图形叫做 Douady 兔子，是由法国数学家 Adrien Douady 发现的。它是一种 Julia 集。
Lee Sallows 最近做了一个网站，收集了很多在几何意义上也成立的幻方，集数学与艺术于一体，为传统意义的幻方赋予了新的生命。大家来欣赏一下吧。
这是一个幻方，它由九块积木组成。这些积木所含的小方格数分别是 2, 6, 8, 10, 12, 14, 16, 18, 22，每行每列和两对角线上的方格总数都是 36 。 牛 B 的是，每条线上的三块积木正好也都能拼成一个 6 × 6 的矩形。
此 MM 叫做 Vi Hart 。她制作了一系列叫做 Doodling in Math Class 的视频，在 YouTube 上的观看人数都是好几万。在欣赏其无比强大的画图能力的同时，你也将会从一个全新的角度体验到数学的美妙。
Doodling in Math Class – Infinity Elephants