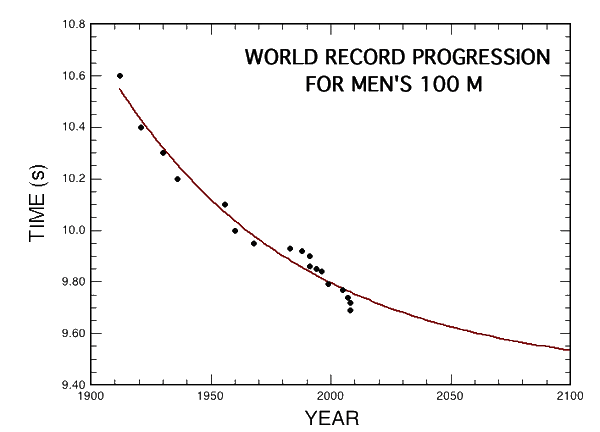
看来,已经有人提前做了一件我最近一直想要做的事情。
最近的几个有点不正常的数据点估计把整条曲线拉低了不少。
来源:http://blog.wired.com/wiredscience/2008/08/bolt-is-freaky.html
统计
立体图与三维数据展示
 我的左眼有相当严重的散光,因此无缘各种类型的3D立体图,包括看对眼、立体眼镜、左右两幅图(一只眼睛看一个)等等。后来,网上出现了一种只需要一只眼睛就能体验的3D图,原理非常简单,效果也比较震撼。只需要在两个眼睛的位置分别拍照,然后做成gif循环显示两个图片,大脑也可以从中迅速获取信息分辨出第三维来。闲逛ffffound时偶然发现这个图,突然想到:同样的方法为何不用于展示三维数据呢?于是试着用Mathematica做了一个。Mathematica输出gif动画相当简单,只需要一句Export[“file.gif”,{g1, g2, …}]就行了。在这里,我们将用三维空间的点来展示组合数的各位数字之和的分布情况。可以看到,使用3D动画的效果非常明显。
我的左眼有相当严重的散光,因此无缘各种类型的3D立体图,包括看对眼、立体眼镜、左右两幅图(一只眼睛看一个)等等。后来,网上出现了一种只需要一只眼睛就能体验的3D图,原理非常简单,效果也比较震撼。只需要在两个眼睛的位置分别拍照,然后做成gif循环显示两个图片,大脑也可以从中迅速获取信息分辨出第三维来。闲逛ffffound时偶然发现这个图,突然想到:同样的方法为何不用于展示三维数据呢?于是试着用Mathematica做了一个。Mathematica输出gif动画相当简单,只需要一句Export[“file.gif”,{g1, g2, …}]就行了。在这里,我们将用三维空间的点来展示组合数的各位数字之和的分布情况。可以看到,使用3D动画的效果非常明显。
img = ListPointPlot3D[
Table[Total[IntegerDigits[Binomial[i, j]]], {i, 0, 50}, {j, 0, 50}],
ViewVertical -> {0, 0, 1}, ImageSize -> 600];
Export["F:\file.gif", {Show[img, ViewVector -> {-32, -20, 60}],
Show[img, ViewVector -> {-31, -21, 60}]}];
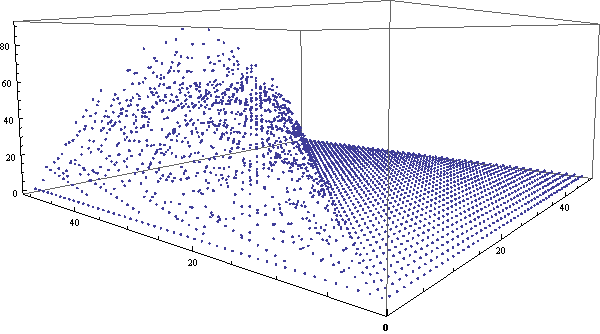
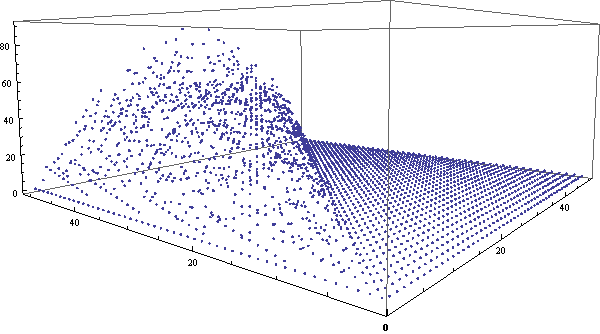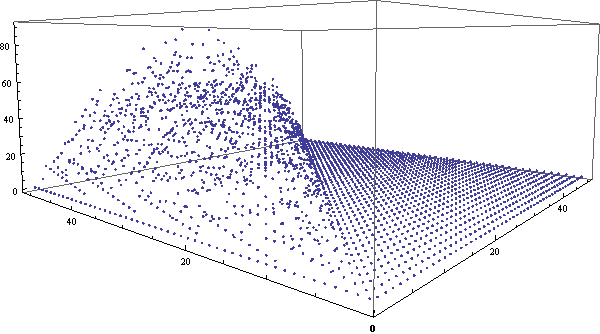
类似地,我们还可以做出环视一周的gif动画来,虽然这样将很难观察出细节,但对总体的把握效果将更好。
设计调查问卷的艺术:怎样才能绝对地保证个人隐私不被泄露
我在学校时,时不时会有人闯进宿舍,给宿舍里的每个人发一张调查表邀请大家填写。如果我不是很忙的话,通常还是很乐意填写的。不过,有时我很悲哀的发现,很多调查表的设计都很缺乏科学性。设计一张合理的调查表并不是一件容易的事情,你需要综合考虑各方面的因素。例如,假如你需要在调查表中问一个极度隐私的问题,尽管你在调查表上再三强调你们的保密措施,但你真的指望所有人都能够如实地回答吗?你真的指望会有人在“我不是处男/处女”或“我有同性恋倾向”前面打一个勾然后把表递到问卷回收人的手中吗?
让我们考虑这样一个问题:你希望在调查表上问一个隐私问题。为了方便起见,假设这个问题只有“是”和“否”两个选项。有什么方案能够绝对地保证个人隐私完全不可能被泄露,让每个人都能够放心地填写,并且问卷回收之后能够得到一个准确的统计结果?
Read more…
Bayesian评分系统:解决样本数量过少引起的问题
本来还打算给这个Blog写一个日志评分系统的,现在看来估计没时间了。之前曾经找过一些关于日志评分系统的资料,偶然在我很喜欢的web 2.0站点TheBroth里找到了一篇介绍Bayesian评分系统的旧文,觉得非常科学,大致翻译一下。
很多网站都有用户评分功能。比如,你可以给某篇文章打分,1分表示这篇文章太烂了,10分表示你爱死这篇文章了。有些网站用加号和减号来代替评分功能。点击“+”表示你喜欢这篇文章,点击“-”表示你不喜欢这篇文章。网站很可能会在首页醒目处加一行黑体二号加粗高亮发光的字,“评价最高的10篇文章”;然后在下面放上平均得分最高的几篇文章的链接,用来吸引点击率。这时,问题就出来了:评分最高的文章不一定真的是评价最高的文章。比如说,某篇文章特别无聊,没一个人评分,然后有个人不小心点错了链接进去了,又一个不小心点到了评分栏上的最后一颗五角星,于是此网站惊现平均得分高达满分的文章;再比如说,某人刚发了一篇文章,然后趁别人还没评分前自己先给自己评几个10分,于是又一篇满分文章横空出世。事实上,可以想到绝大多数新文章刚发表时平均得分不是极高就是极低,这是这种简单的评分机制的一个很突出的问题。应该怎样解决这个问题呢?我们可以分析一下问题的根源,集中思考解决这个问题根源的办法,然后用新的公式来定义一篇文章的最终得分。
问题的根源是什么?问题的根源就是,样本少了会导致结果不可靠。某篇文章的评分人数越少,其平均得分越不可靠,我们应该想办法让得分越靠近所有文章的总平均得分。事实上,评分人数少正说明这篇文章既不受欢迎也没啥争议,它的得分应该接近所有文章的总平均分才对。要是有一种东西能够实现“票少了不算”、“得的票越多对最终得分的影响越大”之类的想法就好了。于是,我们想到了加权平均数。
我们希望得票越少的文章,其得分越接近所有文章的总平均分;得票越多的文章,其得分越接近它本来的平均分。于是我们为所有文章的总平均分和这篇文章的平均分各设一个权值。这篇文章的平均分的权值就是该文的评分人数,这没话说。关键是所有文章总平均分的权值。这可以根据你的喜好来设:权值越小说明你对评分要求越不严格,影响文章得分所需要的票数越少;权值越大说明你越在意样本过少所带来的负面影响,同时说明参与评分的人数一定会很多。因此,这个权值应该由你的网站的总评分人数的多少来决定,用每篇文章的平均评分人数来当权值是一个不错的选择。因此,我们可以用以下公式来算出每篇文章的最终得分:
所有文章的总平均分*每篇文章的平均评分人数 + 这篇文章的平均分*这篇文章的评分人数
文章最终得分 = ———————————————————————————
每篇文章的平均评分人数 + 这篇文章的评分人数
这里,总平均分的权值用的是每篇文章的平均评分人数。你也可以自己设定一个合适的权值。
这种评分方法叫做Bayesian评分。很多web 2.0站点都在用这种评分系统。
顺便记录一下今天的心情。今天我很开心,非常开心:) 原因嘛……秘密
信息学竞赛中可能有用的概率学知识
说到概率,有些好玩的东西不得不提。比如,你知道吗,23个人中至少两个人生日相同的概率竟然超过了1/2;假如你们班上有50个人的话,那更不得了,至少两人生日相同的概率达到97% !如果你会计算这个概率问题的话,你可以亲自证实这一点。本文适宜的读者是知道上述问题怎么算的高中朋友,上述问题也是高中阶段学的一些基本概率知识。
上面的问题都是简单概率,它包含了一个最基本的原则,即使没有系统地学习过,平常人们也都在无形之中使用它:概率等于你要算的东西除以总的数目。比如。我们要计算23个人中任何两个人都不在同一天生的概率。假设2月29日与其它日期出现概率相同的话(这是为了便于计算我们做出的假设,它有悖于常理),那么它的概率为A(366,23)/366^23。它约为0.493677。因此,至少两人在同一天生的概率为1-0.493677=0.506323。当然,对于“你要算的东西除以总的数目”的认识是片面的,比如“投两个骰子出现的数字和从2到12共有11种可能,问数字和大于10的概率”这一问题的答案并不是2/11,因为这11个点数和出现的概率不是相等的,我们只能从投出的两个数字共6*6=36种情况中进行统计,可能的情况只有(5,6)、(6,5)和(6,6) (不会有人说还有(6,7)之类的吧),答案应该是3/36=1/12。这些都是废话,我不细说了。
但是,你有想过这个问题吗:要是这些数目是无穷的怎么办?换句话说,统计的东西不是“离散”的怎么办?比如看这样一个问题。明天早上我要和MM约会,但是具体见面时间我忘了,好像是8:00-9:00的某个时候。那么我随便在这个时段中选一个时间去等MM,最多等她半个小时,正好能见到MM的概率是多少(假设MM先到的话不会等我)。这个问题和我们平时见到的问题不同的地方在于,它的“情况”是连续的,不是离散的,不能逐一统计数目。咋办呢?我们注意到,我的时间随机取一个,MM的时间随机取一个,对于某些组合我们是有缘分的(这些组合无穷多)。这些组合正好对应了平面区域上的点。就是说,搞一个横坐标表示我的时间,纵坐标表示MM的时间,那么肯定能画出那么一块区域,区域里的所有点(x,y)对应所有我和MM可能相见的组合。任何一个时间组合有多大的可能落在这个区域呢?由于在矩形区域内点(x,y)是均匀分布的,我们只需要计算一个面积之比就行了。下图中显而易见,答案是3/8。
一个类似的问题是Buffon投针实验。有一个人,叫Buffon。他在地板上画了很多间隔相同的平行线,然后叫了一帮狐朋狗友来,把一些长度相同的针扔在地上。然后,他统计有多少针和地板上的线相交,并宣称可以得到圆周率π的值。换句话说,一根针投到间隔相同的平行线中,与平行线相交的概率和π有关。我们时常感到数学的神奇之处,比如当这个π在很多不该出现的场合莫明其妙的出现时。例如,Stirling近似公式(黑书上的这个公式写错了)出现了π值:n!≈sqrt(2πn) * (n/e)^n (sqrt是开方的意思)。再比如,两个整数互质的概率是6/(π^2),而无穷级数1+1/4+1/9+1/16+…=(π^2)/6。当然,还有最神奇的e^(πi)+1=0。现在,π又出现在了这样一个看似与圆周率更加没有关系的概率问题中:针与线相交的概率为两倍针的长度除以平行线的间隔再除以π。这个结论的证明和刚才我等MM的问题是一样的。建立这样一个坐标系,x轴是针的中点到离它最近的那根平行线的距离,y轴是针与平行线的夹角。我们一定能做出这样一块“可行区域”,这块可行区域中的点(x,y)所对应的针的位置和平行线相交。然而,这块区域的面积并不像刚才那么简单,它是由一些方程围出来的图形,求这块区域的面积需要使用定积分。这里就不再接着说了,反正能求出来。
当然,涉及无穷的概率问题还有很多其它的统计方法,这里不说明了。
有这么一个笑话。据说一个飞机上有炸弹的概率为十万分之一,但某人并不认为这个概率很小。概率小毕竟意味者可能,每天航班这么多,十万分之一确实不是一个小数目。因此,这个人从来不敢坐飞机。有一次,他居然和朋友上了飞机,朋友吃惊地问,你咋不害怕了。他说,飞机上有一个炸弹的概率不是十万分之一么?那么飞机上同时有两个炸弹的概率就是一百亿分之一了,对吧。朋友说,对,一百亿分之一已经很小了。这人说,那好,我自己已经带了一颗炸弹上来。
从没听过这个笑话的人或许会笑笑说那人真傻,但仔细想想似乎自己解释一下也很困难。这涉及到了条件概率,这在高中课本里(至少在我的高中课本里)没有说过,你把书翻烂了都找不到。
条件概率,顾名思义,就是有条件的概率。比如,有两个炸弹的概率和知道已经有一个炸弹后存在两个炸弹的概率是不同的。假如我们把有两个炸弹的概率记作P(两个炸弹)=百亿分之一,那么后一个问题就是P(两个炸弹|已经有一个炸弹了)。记号P(A|B)就表示在B已经发生了的情况下,A的概率是多少。后面我们可以知道,它仍然等于十万分之一。
换一个问题。还记得最前面我们说的“投两个骰子出现的数字和大于10的概率”这个问题吗?它的答案是3/36。现在改一下,如果我们事先就知道至少有一个骰子是6点。那么概率变成多少了(或者问概率变了没有)?很显然,多了一个条件,概率肯定变大了,笨蛋都知道如果有一个骰子搞出那么大一个点数,那赢的几率肯定增加了。关键在于,前面分析过数字和大于10的情况只有(5,6)、(6,5)和(6,6),它们本来就含有6啊,为什么概率变了。仔细思考发现,原来是总的情况变少了。原来总的情况是36种,但如果知道其中一个骰子是6点的话,情况数就只有11种了。概率变成了3/11,大了不少。我们还需要补充,如果把我们“至少有一个骰子是6点”换成“至少有一个骰子是5点”的话,总的情况数还是11,但3/11将变成2/11,因为有一种情况(6,6)不满足我的已知条件。我们可以纯粹用概率来描述这一个思考过程。如果P(E)表示点数和大于10的概率,P(F)表示至少有一个5点的概率,那么我们要求的是P(E|F),即已知F发生了,求E发生的概率。于是P(E|F)=P(E∩F)/P(F)。这就是条件概率的公式。简单说明一下就是,E∩F表示满足E的情况和满足F的情况的交集,即同时满足E和F的所有情况。P(E∩F)就是E和F同时发生的概率。这个公式使用原来的非条件概率(总情况数目还是36时的概率)之比来表示条件概率(相当于分式同时除以一个数,就如P(E|F)=2/11=(2/36)/(11/36))。回到炸弹问题上,P(A|B)就应该等于出现两个炸弹的概率除以出现一个炸弹,他仍然等于一个炸弹的概率。
高中课本里对“独立事件”的定义是模糊的。其实,现在我们可以很好地给独立事件下定义。如果事件E和事件F独立,那么F就不能影响E,于是P(E|F)=P(E)。把P(E|F)展开,就成了P(E∩F)/P(F)=P(E),也即P(E∩F)=P(E)*P(F)。这不就是“两个独立事件同时发生的概率”的计算公式么。
条件概率的应用很广泛,下面举个例子。
有两个人,他们每三句话只有一句是真的(说真话的概率是1/3)。其中一个人说,Matrix67是女的。另一个人说,对。那么,Matrix67的确属于女性的概率是多少?
这是一个条件概率问题。如果P(E)表示Matrix67是女性的概率,P(F)表示第二个人说“对”的概率,那么我们要求的就是P(E|F),即在第二个人回答后的情况下第一个人说的话属实的概率。按照公式,它等于P(E∩F)/P(F)。P(E∩F)是说,Matrix67是女的,第二个人也说对,表示的实际意义是两个人都说的真话,他的概率是1/3 * 1/3=1/9。P(F)表示第二个人说“对”的概率,这有两种情况,有可能他说对是因为真的是对的(也即他们俩都说真话),概率仍是1/9;还有一种可能是前一个人撒谎,第二个人也跟着撒谎。他们都说谎的可能性是2/3 * 2/3 =4/9。没有别的情况会使第二个人说“对”了,因此P(F)=1/9+4/9=5/9。按照条件概率的公式,P(E|F)=P(E∩F)/P(F)=(1/9) / (5/9)=1/5。后面我们接着说,这其实是Bayes定理的一个非常隐蔽的形式。
你或许看过我的这篇日志:http://www.matrix67.com/blog/article.asp?id=87。我用相当长的篇幅介绍了Monty Hall问题。下面所要讲的东西与这个有关,建议你先去看看那篇日志。不看也没啥,我把题目意思在下面引用一下。
这个问题最初发表在美国的一个杂志上。美国有一个比较著名的杂志叫Parade,它的官方网站是http://www.parade.com。这个杂志里面有一个名字叫做Ask Marylin的栏目,是那种“有问必答”之类的一个Q&A式栏目。96年的时候,一个叫Craig.F.Whitaker的人给这个栏目写了这么一个问题。这个问题被称为Monty Hall Dilemma问题。他这样写到:
Suppose you're on a game show, and you're given the choice of three doors. Behind one door is a car, behind the others, goats. You pick a door, say number 1, and the host, who knows what's behind the doors, opens another door, say number 2, which has a goat. He says to you, "Do you want to pick door number 3?" Is it to your advantage to switch your choice of doors?
这个问题翻译过来,就是说,在一个游戏中有三个门,只有一个门后面有车,另外两个门后面是羊。你想要车,但你不知道哪一个门后面有车。主持人让你随便选了一个门。比如说,你选择了1号门。但你还不知道你是否选到了车。然后主持人打开了另一扇门,比如2号。你清楚地看到2号门后面是一只羊。现在主持人给你一个改变主意的机会。请问你是否会换选成3号门?
对于这个问题,Marylin的回答是:应该换,而且换了后得到车的概率是不换的2倍。
对于这个问题,十年来涌现出了无数总也想不通的人,有一些冲在最前线的战士以宗教般的狂热传播他们的思想。为了说服这些人,人们发明创造了十几种说明答案的方法,画表格,韦恩图,决策树,假设法,捆绑法(我的那篇日志里也提到一种最常见的解释方法),但是都没用。这群人就是不相信换了拿到车的概率是2/3。他们始终坚定地认为,换与不换的概率同为1/2。下面,我们用一个更科学的方法来计算换了一个门后有车的概率。我们使用刚才学习的条件概率。
上面的图表形象地表明了打开某个门的概率是几分之几。横坐标是选择的第几个门,纵坐标是门后面车与羊的排列。对于有些情况(非主对角线上的格子),主持人打开哪个门只有一种选择,我们把它标在这个格子上;对于对角线上的格子,打开门有两种选择,这两种选择出现的几率相等,因此我们用一条斜线划开。现在,还是假设我们选了1号门,那么此时我选到车的概率显然是1/3,同时,这个车在2号门后面的概率也是1/3,在3号门后面仍为1/3。当主持人打开了第2扇门后,我们需要计算一下这导致原来的这些1/3都变成了什么。我们要求在已经知道主持人亮出二号门后面的羊后车在这三个门后面的概率分别是多少。由于我“最初选择1号门”是整个问题的一个假设(大前提),因此对概率的计算只在我们图表中的第一列进行。我们用事件A、B、C分别表示车在1、2、3号门后的概率,事件D表示主持人打开了2号门。在第一列中,打开2号门的情况占了一格半,因此P(D)=1.5/3。A∩D和C∩D的部分分别用灰色和紫色画了出来,B∩D显然为空集。于是,P(A|D)=P(A∩D)/P(D)=(0.5/3) / (1.5/3)=1/3,结果1号门后面有车的概率仍然是1/3。显然,P(B|D)变成0了,因为P(B∩D)=0,B和D根本不可能同时发生。我们惊奇地发现,3号门后面有车的概率从1/3增加到了2/3,因为P(C|D)=P(C∩D)/P(D)=(1/3) / (1.5/3)=2/3。我们使用条件概率从理论上再一次得到了这个雷打不动的事实。
我们最后看一个问题。这个问题是条件概率的终极应用,是概率学中一个最重要,应用最广的东西。把下面这个问题搞明白了,从此对概率学的学习就真正入门,可以摆脱“初级”、“菜鸟”的称号了。这就是传说中的Bayes定理。我已经写了五千字了,不想再写了,这保证是我想说的最后一个东西。
首先你得知道,P(A|B)和P(B|A)是截然不同的两个概念。有些条件概率,正着算P(A|B)容易,把条件反过来算P(B|A)却无从下手,而人们往往更加关心P(B|A)。生活中有很多这样的例子,我们小举一个。
某个地区性病传播飞快,性病患者高达15%。医院临床实验表明,对有性病的人检测,有95%的人显阳性;对没有性病的人检测,有2%的人阳性。现在,假如某个人搞了一个小MM,突然有点担心,跑到医院去检测,查出了阳性。那么他确实有性病的概率是多少?
假如事件A是显阳性,B是有性病,我们可以看到在现实生活中P(A|B)比P(B|A)更容易得到。P(A|B)表示对有性病的人进行检测搞出阳性的概率,这可以通过医院里的抽样统计得到,题目中已经说了是95%。但是,P(B|A)就不好说了,它表示对于某个人来说,显阳性意味者真的有性病的概率是多少。这是针对个人的,统计资料通常没有这一项,但人们却往往更关心这个问题。事实上,我们可以通过已有的条件把P(B|A)算出来。把P(B|A)展开,它等于P(B∩A)/P(A),而因为P(A|B)=P(A∩B)/P(B),把P(B)乘过去,得到P(B∩A)=P(A∩B)=P(A|B)*P(B)。我们把分子的部分转换成了已知量P(A|B)和P(B)的乘积,它等于95% * 15%。那么P(A)怎么算呢?P(A)是由两种情况构成的,可能是有性病的人显的阳性,即P(A∩B);也可能是没有性病的人显的阳性,即P(A∩~B)。~B表示B的补集,也可以在B上面画一条横线表示,我这里画不出来,算了。~B就是没有病的人,它的概率是1-15%=85%。P(A∩B)和P(A∩~B)都可以用已有的概率算出来,分别是刚才得到的P(A|B)*P(B),以及用类似的方法得到的P(A|~B)*P(~B)。。因此整个概率就等于(95% * 15%)/(95% * 15% + 2% * 85%)≈0.8934。这就是Bayes定理的一个具体应用。
在上面的题里,我们求P(A)时把“显阳性”按照“是否有病”分成了两个不相交的部分,并分别求
出概率后再求和。事实上,对于事件A可以按照B的属性分成多个不相交的部分。此时再完整地叙述一下Bayes定理,大家就不难理解了。如果B1、B2、B3一直到Bn是n个互不相交的事件,而且这n个事件是“一个完整的分类”(即并集是全集,包含了所有可能的情况),那么有公式:
P(B1|A)=[ P(A|B1)*P(B1) ]/[P(A|B1)*P(B1) + P(A|B2)*P(B2) + …+ P(A|Bn)*P(Bn)]
下面再举一个例子。这个例子和前一个例子非常相似。事实上,它也和前面说我是女的的那个例子如出一辙。它将是我们的最后一个例子,并且我不给解答,写完例子立马走人。解决这个问题有助于理解和联系前面这两个例子。
我经常约同学单独出去玩。据统计,和一个女同学出去玩的概率高达85%,和一个男同学出去的概率只有15%。现在,某人宣称他看到昨天我和某某男在外面玩。长期观察表明,这人的可信度(说真话的概率)为80%。那么,我昨天真和一个男的出去玩的概率是多少?
Matrix67原创
做人要厚道,转贴请注明出处