Alice 的手中有 n 件物品,每件物品的价值都是一个 1 到 n 之间的整数; Bob 的手中也有 n 件物品,每件物品的价值也都是 1 到 n 之间的整数。现在,两人想要进行一次等值的交易,即 Alice 从自己手中拿出至少一件物品, Bob 从自己手中拿出至少一件物品,使得两人所拿出的物品总价值相等。求证:这是总能办到的。
组合数学
Hofstadter的非线性递推数列
在著名奇书 Gödel, Escher, Bach: An Eternal Golden Braid 的第五章中,为了展现出递推序列的神奇之处,作者 Douglas Hofstadter 定义了这么一个递推序列: G(n) = n – G(G(n – 1)) ,其中 G(1) = 1 。这个序列的前 30 项如下:
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| G(n) | 1 | 1 | 2 | 3 | 3 | 4 | 4 | 5 | 6 | 6 | 7 | 8 | 8 | 9 | 9 | 10 | 11 | 11 | 12 | 12 | 13 | 14 | 14 | 15 | 16 | 16 | 17 | 17 | 18 | 19 |
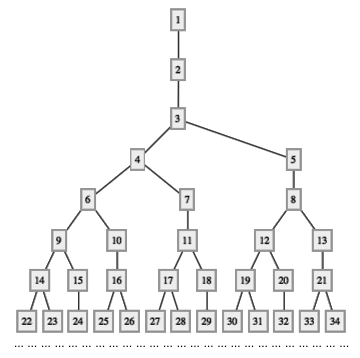
这个数列通常被称作 Hofstadter G-sequence 。它有什么特别的地方呢?如上图,如果把每个标号为 n 的结点都连接到标号为 G(n) 的结点下方,这样的话你将会得到一棵树。从第二行开始算起,各行的结点个数依次为 1, 1, 2, 3, 5, 8, 13, … 正好是著名的 Fibonacci 数列(头两个数都是 1 ,从第三个数开始,每个数都是前两个数之和)。如果我们把第 i 个 Fibonacci 数记作 Fi 的话,上面的规律可以重新表述为:当 n ≥ 2 时,这棵树的第 n 行的结点总个数为 Fn-1 。另外,这棵树的前 n 行的结点总数(也就是第 n 行最右边那个结点的编号)正好等于 Fn+1 ,也是一个个的 Fibonacci 数。对照上面两个事实,你会惊奇地发现,莫非 F1 + F2 + … + Fn-1 + 1 总是等于 Fn+1 ?事实的确如此,上面这个式子对于所有大于等于 2 的正整数 n 均成立。
趣题:证明所有乘积的总和与分拆的方式无关
有 1000 枚硬币堆在一起。把它们任意分成两堆,并计算出这两堆的硬币数的乘积。然后,任意选择其中的一堆硬币,把它继续分成两个更小的堆,并计算出这两堆的硬币数的乘积。不断这样做下去,直到最后每堆都只剩一枚硬币为止。求证:把途中产生的所有乘积全部加在一起,结果是一个定值,它不随分法的改变而改变。
趣题:八根并排放置的水管
下面这个有趣的问题来自于 2012 年 4 月的 IBM Ponder This 谜题。
有 8 根很长的并且颜色不同的水管并排放在一起, A 、 B 两人分别位于这些水管的两端。两个人手中各有若干根很短的橡皮管,他们可以用这些橡皮管任意连接自己这一侧的水管口。 A 的旁边还有一个水龙头, A 可以用橡皮管把水龙头与自己这一侧的其中一个水管口相连。
A 、 B 两人各将获得一个五位 01 串,然后两人可以根据自己手中的 01 串来连接水管口。当 A 打开水龙头后,容易看出,水必然会从其中一侧流出。两人需要保证,如果两人手中的 01 串相等,则水从 A 的一侧流出,否则水从 B 的一侧流出。他们事先可以商量一个策略,但游戏一旦开始,两人一旦拿到各自的 01 串之后,就不允许再交流了(因此两人都不知道对方手中的 01 串是什么)。请你想出一个能保证两人获胜的策略。
Fibonacci数列性质的组合证明
数列 1, 1, 2, 3, 5, 8, 13, 21, 34, … 叫做 Fibonacci 数列。这个数列有很多神奇的性质,其中一个性质是,每一个 Fibonacci 数的平方与它前后两个 Fibonacci 数的乘积一定正好相差 1 。具体地说,如果把第 n 个 Fibonacci 数记做 Fn ,那么有:
Fn+1 · Fn+1 – Fn · Fn+2 = (-1)n
今天看到了这个定理的一个组合数学证明,觉得非常有意思,在这里和大家分享。