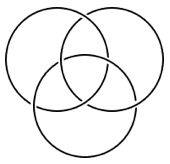
下图中的图 (a) 是由三个绳圈组成的。这是一个非常经典的图形，叫做 Borromean rings 。 Borromean rings 有一个非常神奇的特点：它们是套在一起的，没有哪个绳圈能从中取出来；但是，仔细观察你会发现，每两个绳圈之间都并没有直接套在一起！
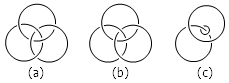
Borromean rings 还有一个听上去更离奇的性质：如图 (b) 所示，如果把其中任意两个绳圈真的套在一起，那么第三个绳圈就会自动脱落掉！为了看出这一点来，我们可以像图 (c) 那样，把其中一个绳圈缩小，让它紧紧地裹在另一个绳圈上，这下就很容易看出，它已经不再对第三个绳圈有任何限制作用了。
为了说明“同痕”这一概念直观上并不容易把握，《The Knot Book》一书中举了一个经典的例子。如下图，左图是一个有三个洞的立体图形，右图是被挖出了三条通道的立方体（但其中一个通道在另一个通道上缠绕了一圈）。令人难以置信的是，两者之间竟然是同痕的，换句话说前者可以连续地变形成为后者。你能想象出这个变换过程吗？
下图中的三个绳圈套在一起，没有哪一个绳圈能从中分离出来。不过，真正有趣的是，如果去掉其中任意一个绳圈，那么其他所有的绳圈都全部散开了。如果 n 个绳圈套在一起，并且任意去掉其中一个绳圈都会同时解开其他所有套着的绳圈，我们就把它叫做 n-component Brunnian link 。
你能想出一个 n = 4 的 Brunnian link 吗？ n = 5 呢？ n 可以任意大吗？