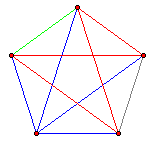
一个完全图K_n是指一个有n个顶点的图，其中每两个点之间都有一条边相连。一个完全二分图是指这样一种图，图中的顶点分为两个点集L和R，L里的每个顶点都和R里的所有点相连。上图显示了一种把K_5划分为四个完全二分图的方法（分别用红蓝绿灰四种颜色来表示这四个子图）。你觉得，最少可以把完全图K_n划分成多少个完全二分图？给出一种划分方案，并证明这个数目已经不能再少了。
算法
趣题：用最少的“并行交换”完成排序
今天是10月25日。祝古汉MM生日快乐。
曾经有一段时间这个Blog的访问量和订阅量剧增，后来才知道因为这个Blog上的一道牛B题目被出成POJ的月赛题了。那道题目真的很好玩，题目和解答都很简单有趣。其实我挺喜欢这种“给出一个算法并证明该算法最优”类型的数学题目。这里再和大家分享一个类似的比较老的题目，有兴趣的话不妨先想想再看答案。
一次“交换”操作是指将数列中的两个数位置对换。我们假设，互不相交的若干个交换操作可以一次同时进行；换句话说，如果k个交换中任两个都不会对同一个数进行操作，那么这k个操作可以并行完成。例如，在数列
10, 6, 8, 5, 2, 3, 1, 4, 7, 9
中，我们可以同时交换第4个数和第6个数，第8个数和第9个数，以及第3个数和第7个数。经过这一次“并行交换”后，数列变为：
10, 6, 1, 3, 2, 5, 8, 7, 4, 9
任意给定一个长度为n的全排列，请问对该序列进行排序最坏情况下需要多少次并行交换？给出一种具体的算法，说明这个次数足够了；并且给出一种最坏情况，证明这个次数是必需的。
趣题：只用赋值、自增和循环操作实现减法运算
网友Mingliang Zhu在TopLanguage上发起提问。
设想这样一个计算机系统，它只支持以下几个操作：
1. 定义变量、给变量赋值；
2. 变量自身加一；
3. 令一段语句循环执行指定的次数。
这个系统只处理且只能处理0和正整数。系统不存在“溢出”的问题。
注意这个系统没有比较运算，事实上它甚至不存在Boolean值和判断语句。
循环语句也不是FOR i=a TO b DO的形式，只能是LOOP n的形式。
在这个系统上实现加法很容易，让a自增b次即可。现在的问题是，你能在这个系统上实现减法吗？
停机问题、Chaitin常数与万能证明方法
高中一次英语课上，英语老师问我们，如果你有机会乘坐时光机回到过去，你想利用这次机会来干啥。“人上一百，形形色色”这句老话得到了完美的验证。什么“回去看看四大美女”呀、“看看金字塔是怎么建造的”呀、“回到三年前的那个风雨交加的夜晚握住她的手深情地告诉她其实我不想让你离开我你知道你走了之后我有多么痛苦吗”之类的东西，各种稀奇古怪的想法都被我们说了个遍。我还记得当时我说的啥——一个无比实用的雕虫小技。我说，我就想回到一个星期前，然后去买彩票。发明一个新东西并不是关键，关键是你怎么去使用它。
最奇怪的幻想总是来自于最奇怪的需求。大家有过这种经历吗？看到自己写的程序运行了半天都还没有任何结果，于是开始纠结，到底是再等一会儿呢还是强行终止了检查一下看程序写错没；犹豫了半天决定杀掉进程后，检查了半天又发现程序没有写错。于是开始怨念，早知道程序没有死循环的话刚才就多等一会儿了。此时，你会突然开始幻想，有没有什么编译器能够事先告诉你你的程序是否会无限运行下去？虽然编程判断一段代码是否会无限执行下去很可能会相当的困难，但我们仍然不排除会有某个天才程序员想出了一个比三角恋爱更加复杂的算法，花它五年的功夫为他心爱的编译器写出了这样一个强大的插件。为什么不可能呢？这个东西看上去似乎比时光旅行机更现实一些。或许我们会在某个科幻电影中看到，一个程序员在黑黢黢的屏幕上输入了几个数，敲了一下回车，然后屏幕上立即用高亮加粗字体显示“警告：该输入数据会导致程序无限运行下去，确定执行？(Y/N)”。如果有一天，这一切真的成为了现实，那么你能利用这个玩意儿来做些什么实用的、有价值的事情？如果我说你能靠这玩意儿发大财你相信么？
随机洗牌：哪一种算法是正确的？
记得当年搞NOIp时，我犯过一个相当严重的错误：错误地把Floyd算法的i, j, k三层循环的位置顺序搞颠倒了。直到准备省选时我才突然意识到，Floyd算法应该最先枚举用于松驰操作的那个“中间变量”k，表示只经过从1到k的顶点的最短路；而我却一直习惯性地以为i, j, k应该顺次枚举。令人惊讶的是，这个错误跟了我那么久我居然从来都没有注意到过。后来，我发现有我这种经历的人不止一个。惯性思维很可能会让你接受一些明显错误的算法，并且让你用得坦坦荡荡，一辈子也发觉不了。
假使你需要把一个数组随机打乱顺序进行重排。你需要保证重排后的结果是概率均等、完全随机的。下面两种算法哪一种是正确的？其中，random(a,b)函数用于返回一个从a到b（包括a和b）的随机整数。
1. for i:=1 to n do swap(a[i], a[random(1,n)]);
2. for i:=1 to n do swap(a[i], a[random(i,n)]);