网上有各种直观的排序算法图形化演示(见这里和这里),我自己也曾经做过一个。
今天我看到了一个我所见过的最酷的、最可爱的排序算法演示。
某网站被干掉了后,大家会错过很多精彩的视频。我注册了一个土豆网的帐号,把一些精彩的视频搬过来与大家分享。
算法
记09年北大ACM校内赛
大学生活混起来很快,不知不觉又是一年过去了。去年5月10日的ACM校内赛给我留下了许多美好的回忆,因此今年我主动去报了名(上次是被人给拖去的)。今年有点装怪,题目数量不变,但时间缩短为4个小时。原计划是从8:00做到12:00,结果可能是因为我们所在的7号机房迟迟没有开门,时间临时改成了8:15到12:15。总的来说,今年的题目比去年要糟糕得多,但也不乏一些精彩的题目。
和去年一样,第一题依旧是所有题目中最科学的一道。题目给定一个不超过2000*2000的网格,你在最左下角的位置(即(0,0)点),你的目的地在(x,y)。要求你的路线不得经过同一个交叉点两次,且不允许左转(题目背景让这个条件顺理成章:街道靠右行,左转不方便),问合法的路线共有多少种。题目难点就是你不一定要走最近的路,完全允许你绕上一大圈;这破坏了有序性,很难构造出递推公式或动态规划模型。稍微画一下图,我们发现了一些显然但很有启发性的规律:每一次右转后,你左手边方向的所有区域都不能再走了,这很可能产生出规模更小的子问题来。另外,所有合法路线必然是有如螺旋线一样的一圈一圈绕着终点走,这种隐藏的有序性也为动态规划提供了可能。但顺着这个思路想下去屡屡碰壁,我猜不少队伍都卡在这儿了吧。
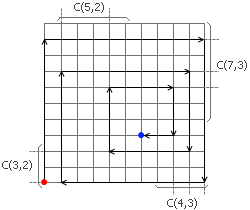
后来我完全打翻前面的全部思路,猛然想到了一个具有决定意义的想法:街道的选取唯一地决定了整个路线。例如,假设我想计算转弯恰好11次的路线有多少条。这样的路线一定含有三条向上走的路、三条向右走的路、三条向下走的路和三条向左走的路。除去第一条路和最后一条路的位置都是确定的,其它的路选在哪一行或者哪一列唯一地决定了整个路线。因此,我们可以用排列组合直接计算出答案来。向上走的路是五选二,向右走的路是七选三,向下走的路是四选三,向左走的路是三选二。把它们各自的选取方案数乘起来就得到了拐弯11次的合法路径。于是,计算所有的路线数只需要从小到大枚举拐弯的次数,每一次计算都是常数的,总复杂度是O(n)的;整个算法的瓶颈反倒是O(n^2)的组合数预处理,不过这个复杂度完全可以承受。
(召集)你能想到的最奇妙的算法题是什么?
昨天和老朋友BY一起吃饭时又一次不可避免地谈到了算法问题。一个有趣的话题是:提起那些最巧妙的、最离奇的牛B算法时,你想到的第一个算法题是什么?
我第一想到的算法题是那道经典问题:n个数中有且仅有一个数出现了奇数次(其它数都出现了偶数次),如何用线性时间常数空间找出这个数。解法也只有一句话:从头到尾异或一遍,结果就是要求的那个数。该问题的加强版也异常牛B,我曾经在这里介绍过。不过,这个算法我在茶余饭后已经聊过无数次了……
脑海中出现的另一个牛B算法题则是POJ3318:给你三个n*n的矩阵A、B、C,问你A*B是不是等于C。数据保证O(n^3)铁定超时,因此你需要想一个不用把A和B乘起来就可以验证的算法。一个基于概率的算法是随机生成一个n乘1的矩阵R,然后判断A*B*R是否等于C*R,而前者相当于A*(B*R),与后者一样都可以在O(n^2)的时间里算出来。如果算出来的结果相等,几乎可以肯定A*B和C也是相等的。
趣题:均匀分布且和为常数的n个变量
不知道大家有没有幻想过,数学中是否存在这样一个牛B的问题,发表出来后十几年硬是没有一个人解开;后来某人惊奇地发现,它有一个极其精妙的解答,整个解决过程只需要几句话就能说清楚,但它实在是太巧妙了,这么多年就没有任何人想到。最近我就遇到了这样的事情。3月份UyHiP的题目非常有趣,整个证明几句话就完了,但想到解法的却只有一人。
题目描述也极其简单。对于哪些n,存在一种生成n个随机变量的算法,使得它们在0和1之间均匀分布,且它们的和是一个常数?更进一步,如果这n个变量中任意k个都相互独立,满足要求的k最大是多少(表示成关于n的函数)?
当然,这道题目我也没想出来。答案公布前,我思考了很久,最后还是放弃了。显然n是偶数时这样的算法是存在的,例如当n=6时,只需要先独立地选取3个随机变量X_1, X_2, X_3,然后令X_4 = 1 – X_1,X_5 = 1 – X_2,X_6 = 1 – X_3即可。这可以保证6个变量之和总为3,且它们均匀地分布在[0,1]区间里。但是当n是奇数时,满足要求的算法就未必存在了。例如当n=3时,不妨让X_1和X_2随机取,X_3等于1.5 – X_1 – X_2。这种算法似乎很和谐,问题就出在X_3有可能不在0和1之间。那么,重复执行该操作直到返回一个落在[0,1]里的X_3呢?这样的话变量又不是均匀分布的了,这将让变量更容易取到中间去,因为X_1和X_2太小或太大往往算不出合法的X_3(下图是Mathematica模拟的结果)。我试图从“n个变量的和的期望值是n/2”出发,证明和为1.5的3个变量不可能均匀分布在0到1之间。不过,最终还是没有找到突破口。
趣题:寻找策略使得总有一人猜出他背上的数
正在上虚词研究课,好友Chain发来短信说,北大BBS化学学院版上发了一道很有趣的谜题,已经上十大热门话题第三了。我也是第一次看到这个题目,和大家分享一下。
话说周一某实验室有16名同学,有一天*老师把大家叫到一起说:下周来做实验的时候,我会给你们每个人背后贴一张纸,纸上的数字从1到16都有可能,不同同学背后的数字可以重复。你们每个人可以看到别人背上的数字,但不能看到自己的数字。贴纸之后你们之间不允许进行任何形式的沟通交流。之后你们排队依次来D***,告诉我你自己背后的数字是多少;由于D***室隔音效果很好,室外的人不能听到室内的同学的说话声(更好的说法是,每个人独自在一张小纸条上写下猜测结果,这就避免了可能由排队猜数的时间和顺序带来的“交流”)。等到16名同学都猜完之后公布结果。只要你们16个人中间能有一个人猜对自己背后的数字,我会让大家都得满分;但如果你们都没有猜对自己背后的数字的话,则你们全部都要重修有机实验。那么你要怎样做才能避免挂科的命运呢?
这道题目很有意思,看答案之前不妨自己先想一下。
提示:先从两个人的情况开始想起。