出了一道好题目却不知道该怎样投递到各大OJ上?现在不用担心这个问题了,因为你可以直接把自己的Blog变成一个OJ。Scarky是一个建立在SPOJ系统上的OJ平台。所不同的是,任何人无需注册便可以编写自己的题目并发在自己的网站上与网友分享,并且网友们提交答案时也不需要进行注册。这个网站的功能还在不断扩充中,但目前就Programming Challenge模块看来,这个网站已经很强大了。以后我有了好题目就用这种方式和大家分享了,这里先试用一下,题目来源好像是某次USACO月赛。
算法
聆听排序算法的声音
在网上偶然看到这篇文章,决定把之前创作排序算法内存状态演示图所用的Mathematica程序修改一下,于是搞出来5个midi音乐。这些midi文件用音高来表示内存状态,初始时的音都是乱的,然后声音渐渐变得有序,最后就成了从低到高的一串音符。
http://www.matrix67.com/data/bubble_8_elements.mid
http://www.matrix67.com/data/insert_8_elements.mid
http://www.matrix67.com/data/select_8_elements.mid
http://www.matrix67.com/data/quick_12_elements.mid
http://www.matrix67.com/data/bogo_6_elements.mid
哪位兄弟能推荐一个在线放midi文件的好方法?
俄罗斯方块可以永无止境地玩下去吗?
大家在玩俄罗斯方块的时候有没有想过这样一个问题:如果玩家足够牛B的话,是不是永远也不可能玩死?换句话说,假设你是万恶的游戏机,你打算害死你面前的玩家;你知道任意时刻游戏的状态,并可以有针对性地给出一些明显不合适的方块,尽量迫使玩家面对最坏情况。那么,你有没有一种算法能保证害死玩家,或者玩家无论如何都存在一种必胜策略呢?注意,俄罗斯方块的游戏区域是一个宽为10,高为20的矩形,并且玩家可以预先看到下一个给出的方块是什么。在设计策略时,你必需考虑到这一点。
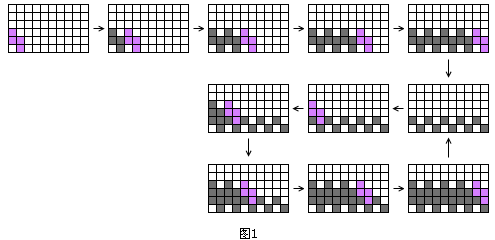
相信很多人有过这样的经历:玩俄罗斯方块时一开局就给你一个“S”型方块,让完美主义者感到异常别扭;结果,第二个方块还是这个“S”,第三个方块依旧是“S”,相当令人崩溃。于是,我们开始猜测,如果游戏机给你无穷个“S”形方块,玩家是不是就没有解了?答案是否定的。如图1,从第10步开始,整个局面产生一个循环;只要机器给的一直都是“S”方块,玩家可以不断重复这几个步骤,保证永远也死不了。

不过,这个循环是在游戏场地清空了的情况下才产生的。有人会进一步想了,要是在玩着玩着,看着你局势不好时突然给你无穷多个“S”方块呢?事实上,此时局面的循环依然可能存在,如图2。在第5个“S”形方块落地后,循环再次产生。
经典证明:推箱子游戏所需步数可达指数级
今天在写一个稿件时又翻阅了一下Erich Friedman的Math Magic,发现了一个有趣的东西——场地大小为n的推箱子游戏所需要的最少步数最坏情况是多少。下面这个构造说明,最坏情况至少也是指数级的。
首先,让我们来看看该构造中的一个基本单元:
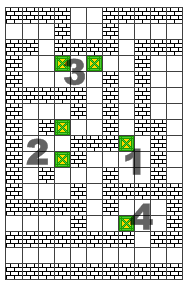
这个构造中共有6个箱子,且它们都已经在目的位置上了。不难看出:
1. 假如你人在这个区域之外,你只可能从右上角的出入口进入该区域,从其它地方进去都会导致死局
2. 从右上角进入后你只能往下走,进入1区;走左边的话直接导致死局
3. 你可以通过2区前往3区,但若从3区左上角的出口出去了,则2区动过的箱子将永远无法回到原位(除非你原路返回)
4. 你可以通过2区前往3区,并把3区左边的那个箱子左移一格,再返回2区;这样下次你再从右上角进入该区域时便可以直接经过3区从左上角出去
5. 最后你只能从4区离开
趣题:构造整数域上的函数f使得f(f(n))等于-n
StackOverflow最近有一个面试题特别火爆:构造一个定义域和值域都是全体整数的函数f使得f(f(n)) = -n。如果你不能设计出函数对于所有n都成立,那就设计函数能够满足尽可能多的数。
一些比较容易想到的解如:
if n > 0:
return -n
else:
return n
不过这个函数只适用于所有非负整数。当然,这并不是我们的最优解。你还能想到更好的办法吗?