2006 年,我在博客(当时还是 MSN Space)上发了 《什么是 P 问题、NP 问题和 NPC 问题》 一文。这是我高二搞信息学竞赛时随手写的一些东西,是我的博客中最早的文章之一。今天偶然发现,这篇现在看了恨不得重写一遍的“科普”竟仍然有比较大的阅读量。时间过得很快。《星际争霸》(StarCraft)出了续作,德国队 7 比 1 大胜东道主巴西,《学徒》(The Apprentice)里的那个家伙当了总统,非典之后竟然出了更大的疫情。现在已经是 2022 年了。这 16 年的时间里,我读了大学,出了书,娶了老婆,养了娃。如果现在的我写一篇同样话题的科普文章,我会写成什么样呢?正好,我的新书《神机妙算:一本关于算法的闲书》中有一些相关的内容。我从书里的不同章节中摘选了一些片段,整理加工了一下,弄出了下面这篇文章,或许能回答刚才的问题吧。
算法
称假币问题的变形:无假币与“天平机”
大家应该听说过 9 枚硬币的问题吧。9 枚硬币当中有 8 枚是真币,有 1 枚是假币。所有的真币重量都相同,假币的重量则稍重一些。怎样利用一架天平两次就找出哪一枚硬币是假币?方法是,先把 9 枚硬币分成三组,每组各 3 枚硬币。然后,把第一组放在天平左边,把第二组放在天平右边。如果天平向左倾斜,说明假币在第一组里;如果天平向右倾斜,说明假币在第二组里;如果天平平衡,说明假币在剩下的第三组里。现在,假币的嫌疑范围就被缩小到 3 枚硬币之中了。选择其中 2 枚硬币分放在天平左右两侧。类似地,如果天平左倾,就说明左边那枚硬币是假的;如果天平右倾,就说明右边那枚硬币是假的;如果天平平衡,就说明没放上去的那枚硬币是假的。
9 硬币问题实在是太经典了,你甚至能在人教版小学五年级下册的课本里看到它。9 硬币问题还衍生出了很多变形,其中最著名的当属 12 硬币问题了:有 12 枚硬币,其中一枚是假币,但我们不知道假币是更重一些还是更轻一些;请利用一架天平三次找出哪一枚硬币是假币,并判断出它比真币更重还是更轻。12 硬币问题的经典程度恐怕不亚于 9 硬币问题。早在 20 世纪 40 年代,12 硬币问题就已经吸引了一大批数学家和数学爱好者,甚至有人建议把这个问题扔到德国去,以削弱德国人在二战中的战斗力。如果你想知道答案,可以在网上找找,应该很容易找到。我们今天就不讨论了。
今天,我们真正想聊的其实是这个问题的另外一种比较少见的变形:仍然是要在 9 枚硬币当中寻找 1 枚假币,仍然假设假币的重量要稍重一些,仍然只能使用天平两次;但是这一次,你所使用的是一种“天平机”,它不会立即告诉你现在是哪边重哪边轻,而是在你两次称完后把这两次的结果一并打印给你。这下,你就没法根据天平的反馈结果随机应变了,必须事先把每次怎么放硬币全规划好。那么,你该怎么办?在本文后面的内容中,均已知假币比真币更重,直至另有说明。
趣题:为什么偏偏是 6 格?
无穷多个相同大小的正方形格子排成一排,向左右两边无限地延伸。每个格子里都有 0 个、 1 个或多个原子。每一次,你可以对它们做下面两种操作之一:
- 选择某个格子,保证该格子内至少含有 1 个原子。将该格子内的其中 1 个原子分裂为 2 个,从而使得该格子内的原子数量减 1 ,两边的邻格里的原子数量分别加 1。
- 选择某个格子,保证两边的邻格里均至少含有 1 个原子。从两边的邻格里各取 1 个原子聚合起来,从而使得两边的邻格里的原子数量分别减 1 ,该格子内的原子数量加 1。
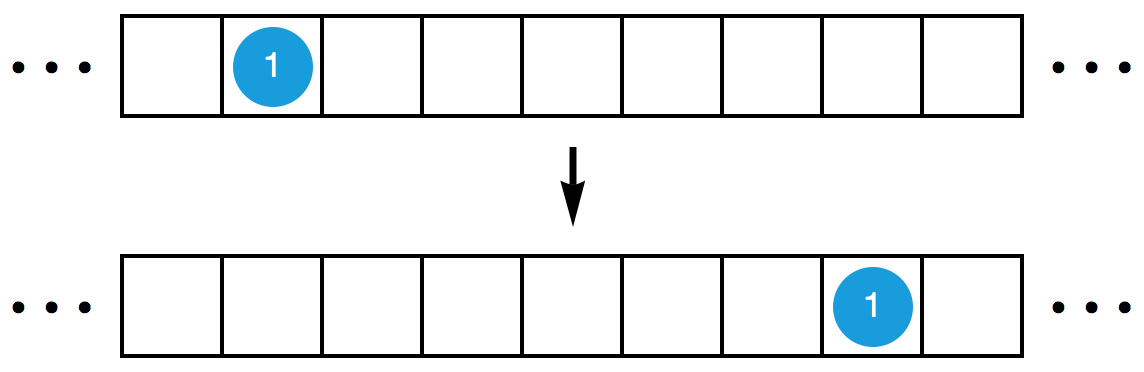
初始时,某个格子里有 1 个原子。现在,你需要在若干次操作之后,让它右移 6 格。也就是说,你需要用若干次操作把下面的第一个图变成第二个图(其中,数字 1 表示该格内的原子数为 1 )。继续阅读下去之前,你不妨自己先试一试。你可以在纸上画好格子,用硬币、大米、巧克力豆等物体代替原子。
捡石子游戏、 Wythoff 数表和一切的 Fibonacci 数列
让我们来玩一个游戏。把某个国际象棋棋子放在棋盘上,两人遵循棋子的走法,轮流移动棋子,但只能将棋子往左方、下方或者左下方移动。谁先将棋子移动到棋盘的最左下角,谁就获胜。如果把棋子放在如图所示的位置,那么你愿意先走还是后走?显然,答案与我们放的是什么棋子有关。
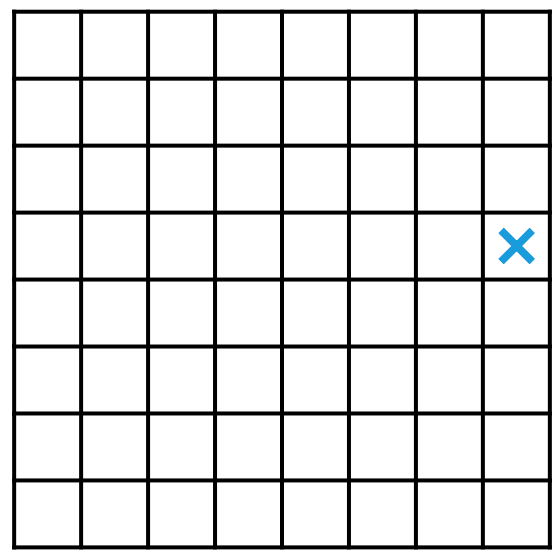
这个游戏对于兵来说是没有意义的。在如图所示的地方放马或者放象,不管怎样都无法把它移动到棋盘的最左下角,所以我们也就不分析了。因此,我们只需要研究王、后、车三种情况。
趣题:如果每次只增加一个区域的话
著名的四色定理(four color theorem)告诉我们,如果一个地图由若干个连通区域构成(没有飞地),那么在给每个区域染色时,为了让相邻区域的颜色不同,最多只需要四种颜色就足够了。不过,这个结论成立有一个条件:整个地图已经事先确定了。如果我们每次只增加一个区域的话呢?具体地说,如果每次你给一个区域染色之后,我再画出下一个区域,并且之前已经染好颜色的区域不能再修改了,那么四种颜色还足够吗?这里,我们假设,在染色时,你总是遵循一个非常朴素的贪心策略:用第一个合法的颜色给每个新的区域染色。下面这个例子告诉我们,在这些假设下,四种颜色就不够了,有时五种颜色是必需的。

我们的问题就是,在这些假设下,五种颜色就一定够吗?有没有可能构造出某个情况,使得六种颜色是必需的?有没有可能构造出某个情况,使得七种颜色是必需的?