Mathematica 强大的符号计算和化简能力相信会让不少人震撼不已。输入 Sum[1/n^2, {n, 1, ∞}] ， Mathematica 竟然知道它等于 π^2/6 。我不禁问自己， Mathematica 真的什么都能化简出来吗？今天，我偶然遇到一个简单的表达式， Mathematica 竟然不知道它的精确值。
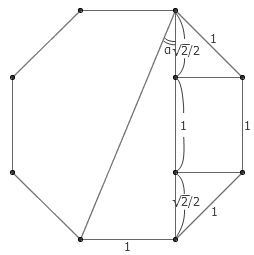
在 Mathematica 中输入 Cot[π/2] ， Mathematica 会告诉你它等于 0 ；在 Mathematica 中输入 Cot[π/4] ， Mathematica 会告诉你它等于 1 ；但在 Mathematica 中输入 Cot[π/8] ， Mathematica 返回的却还是一个 Cot[π/8] ，并没有给出它的值。而 Cot[π/8] 并不是一个复杂到无法用四则运算和平方开方表达出来的数。在一个边长为 1 的正八边形中，每条边的所对应的“圆心角”为 2π/8 = π/4 ，因此“圆周角” α 就等于 π/8 。由下图我们可以轻易看出， Cot[π/8]=√2+1 。
Alphametic 是指这样一种有趣的文字游戏。在一个用字母组成的加法算式中，相同的字母代表相同的数字，不同的字母代表不同的数字。如果算式成立，那么这个数字谜有唯一解。而 Alphametic 的精髓就在于，整个算式本身也必须“有意义”。最经典的 Alphametic 可能是这个：
SEND + MORE = MONEY
它的唯一解是 9567 + 1085 = 10652 。
就像灯谜、对联一样，作为一种文字游戏， Alphametic 也有很多异常牛 B 的，比如：
EARTH + AIR + FIRE + WATER = NATURE
1969 年，有人发现了这样一个有趣的 Alphametic：
THREE + THREE + TWO + TWO + ONE = ELEVEN
这样的 Alphametic 叫做 Doubly-True Alphametic 。可以证明上面这个 Doubly-True Alphametic 是合法的 Alphametic 中“最小的”一个。一个稍微大一点的 Doubly-True Alphametic 为：
SEVEN + SEVEN + SIX = TWENTY
IBM Ponder This 上个月的题目很有意思：利用各种数学函数和数学符号，用两个数字 2 得到一个 5 。不过，有一些限制条件：
1. 只能够使用两次数字 2 。因此，像 2 + 2 + 2/2 这样的算式是不行的。
2. 不允许使用变量，因此 (2x + 2x + x)/x 也是不合法的。
3. 不允许使用其它常量，因此 2 + 2 + ln(e) 是不合法的，因为用到了常量 e 。诸如 (2+i)(2-i) 的妙解也因此被禁止了。
4. 不允许使用取整类的函数，否则问题就太简单了，例如⌈√(2*2)!⌉。
电子公告板上的式子原本是正确的，只是因为有一个像素点坏了，才显示出如此荒谬的结果。
你能看出是哪一个像素点坏了吗？
题目来源：http://www.braingames.ru/?path=comments&puzzle=393
答案很简单，这里就不公布了……