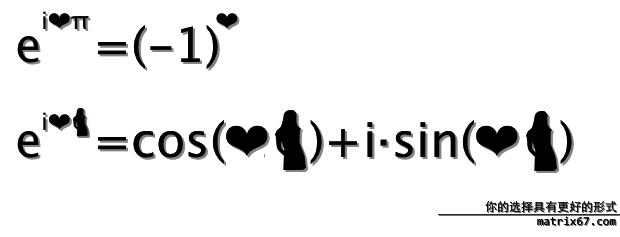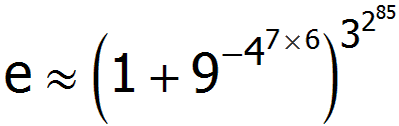你是否很小就注意到了下面这两个有趣的算术现象？这两个简单的算术谜题是否一直都困扰着你？今天，大家终于有机会解开谜团了。
问题一： 2 加 2 等于 4 ， 2 乘 2 也等于 4 。还有其他的整数对，它们的和与积也相等吗？
我们要求的就是 m + n = mn 的整数解。方程可以变为 mn – m – n + 1 = 1 ，也就是 (m – 1)(n – 1) = 1 。由于 m 、 n 都是整数，因此 m – 1 和 n – 1 也都是整数。两个整数之积为 1 ，只有两种情况——这两个数都是 1，或者这两个数都是 -1 。前者对应了 m = 2, n = 2 ，后者解出来则是 m = 0, n = 0 。如果把 (0, 0) 看作平凡解（或者如果我们把问题限制在正整数范围）的话，非平凡解就只有 (2, 2)，没有其他的了。
最近看到几个有趣的数学谬证，想写下来与大家分享；结果写到这个又想到那个，一写就写个没完，于是想到干脆做一篇谬证大全，收集各种荒谬的证明。
如果你有什么更棒的“证明”，欢迎来信与我分享，我会更新到这篇日志中。我的邮箱是 matrix67 at tom.com ，或者 gs.matrix67 at gmail.com 。
1=2？史上最经典的“证明”
设 a = b ，则 a·b = a^2 ，等号两边同时减去 b^2 就有 a·b – b^2 = a^2 – b^2 。注意，这个等式的左边可以提出一个 b ，右边是一个平方差，于是有 b·(a – b) = (a + b)(a – b) 。约掉 (a – b) 有 b = a + b 。然而 a = b ，因此 b = b + b ，也即 b = 2b 。约掉 b ，得 1 = 2 。
这可能是有史以来最经典的谬证了。 Ted Chiang 在他的短篇科幻小说 Division by Zero 中写到：
There is a well-known “proof” that demonstrates that one equals two. It begins with some definitions: “Let a = 1; let b = 1.” It ends with the conclusion “a = 2a,” that is, one equals two. Hidden inconspicuously in the middle is a division by zero, and at that point the proof has stepped off the brink, making all rules null and void. Permitting division by zero allows one to prove not only that one and two are equal, but that any two numbers at all—real or imaginary, rational or irrational—are equal.
这个证明的问题所在想必大家都已经很清楚了：等号两边是不能同时除以 a – b 的，因为我们假设了 a = b ，也就是说 a – b 是等于 0 的。
刚才看到这个很漂亮的无理数 e 的近似表达，它恰好用到了 1 到 9 这 9 个数字。
猜猜看它能精确到 e 的小数点后多少位？ 10 位？ 100 位？ 1000 位？ 10000 位？
或许有人会对算式 5^2 = 25 有一种特别的偏好——等式左右两边都用到了相同的数字，让人深感奇妙。类似的算式还有很多，例如
5^(6 – 2) = 625
(4 / 2)^10 = 1024
((86 + 2 * 7)^5 – 91) / 3^4 = 123456789
我们自然而然地提出了这样一个问题：这样的算式究竟有多少呢？答案是：无穷多。只需要借助本文一开始提到的算式 5^2 = 25 ，我们就能轻易构造出无穷多个同样满足这种神奇性质的算式来：
50^2 + 0 = 2500
500^2 + 0 + 0 = 250000
5000^2 + 0 + 0 + 0 = 25000000
……
现在，让我们来看看另一类更加精妙的算式：等式两边的数字顺序也完全一样！
– 1 + 2^7 = 127
(3 + 4)^3 = 343
16^3 * (8 – 4) = 16384
这样的算式是否仍然有无穷多个呢？