一、平面三圆问题1
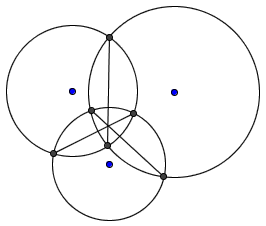
问题:平面上三圆两两相交于六点。试证明三条公共弦共点。
证明:把这三个圆想像为三个球的大圆。为方便叙述,我们把三个球的球心确定的平面记作 α。显然,平面 α 在三个球上的截面就是题目的这三个大圆,而 α 上的三个大圆的三条公共弦即是每两个球之间的公共小圆在 α 上的投影。我们要证明的就是三个公共小圆在平面 α 上的投影共点。注意到三个球交于两点,这两点关于平面 α 对称且这两点就是三个公共小圆的交点。把这两点也投影到平面 α 上,得证。
二、平面三圆问题2
问题:在平面三个圆中,任意两个圆都有两条公切线且两条公切线交于一点。显然,这样的点有三个。试说明这三点共线。
证明:在这个平面的三个圆上放三个球,每个球的半径都等于它底下的那个圆的半径。显然,这个平面是这三个球的一个公切面。再把公切线想像成这三个球确定的三个圆锥的母线在平面上的投影。显然三个圆锥的顶点都在这个平面上,且这三个顶点就是待证共线的三点。这三点是显然共线的,因为我们可以在三个球上找到另一个公切面(想像一块玻璃板从上面盖下去),那么这个切面上也包含了三个圆锥的顶点,而这两个切面的交线是唯一的一条直线。
三、四人旅行问题
问题:平面上四条直线,任两条不平行,任三条不共点。四个旅行者 A、B、C、D 分别匀速地走在这四条直线上(他们的速度可以不相同)。若 A 在行走过程中与 B、C、D 相遇,B 在行走过程中与 C、D 相遇(当然也遇见了 A),求证:C、D 在行走过程中相遇。
证明:作垂直于平面的直线作为时间轴,建立三维直角坐标系。由于四人均匀速行走,因此他们的路程-时间图像是线形的。我们可以在空间中作出 A、B、C、D 四个人行走路程与时间关系的图像并分别命名为 La、Lb、Lc、Ld。这样,我们可以从这四条空间直线中轻易判断某一时刻四人的位置。例如,空间中 P 点 (x, y, t)在直线 Lc 上,则表明在 t 时刻 C 走到了平面(x, y)位置。好,现在强了,真的强了。A、B 不是曾经相遇过吗?这就是说,La 和 Lb 相交。这两条相交直线可以确定一个平面。C 不是与 A、B 都相遇过吗?那就是说,Lc 与 La、Lb 都相交。于是,Lc 也在这个平面上。同样地,Ld 也在这个平面上。既然全部都共面了,Lc、Ld 必然会相交,即 C、D 必相遇。得证。
四、三角形对称问题
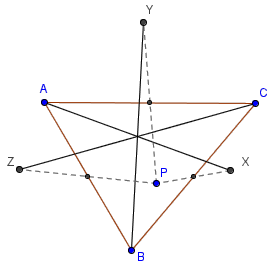
问题:平面上任意三角形 ABC 和异于 A、B、C 三点的点 P。 X、Y、Z 三点分别是 P 点关于三边 BC、AC、AB 的中点的对称点。求证:AX、BY、CZ 共点。
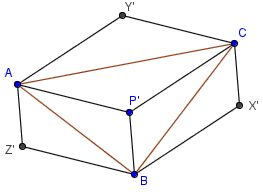
证明:考虑空间中一点 P' 使 PP' 垂直于平面 ABC。作出 X'、Y'、Z' 关于三边 BC、AC、AB 的中点对称。可以得到,点 A、B、C、P'、X'、 Y'、Z' 是一个平行六面体的顶点。AX'、BY'、CZ' 是三条体对角线,他们显然共点。这个证到了有什么用呢?把这几个带了一撇的点全部投影到平面 ABC 上,结论就证到了。