前两篇文章中,我们提到了两个用杠杆原理解决数学问题的例子。这篇文章将从另一个物理领域出发,探索光学的一个重要原理与几何极值问题的关系。
物理学的美不仅仅表现在简洁的公式上。我们还惊奇地发现,很多物理现象都是按照使某个变量达到极值的方式发生。一个典型的例子就是Fermat原理,它指出了光的传播路径的一个重要规律:光总是沿着所花时间最短的路径传播。这里我们将简单介绍一下Fermat原理,该系列后面的文章里将会用到这一原理。
Fermat原理俗称“最快到达原理”、“最小时间原理”,意思是光线传播的路径总是满足这样一个规律:它总能使光在最短的时间内到达目的地。这个原理完美地统一了直线传播定律、反射定律和Snell定律,解释了为什么光线总是沿直线传播,为什么入射角等于反射角,以及光线在不同介质间传播为什么会发生折射现象。
在Ted Chiang的著名科幻小说The Story of Your Life里有这样一段形象的描述:
“好,这是一条光线从空气射进水中所走的路线。在碰到水面前,光线沿着直线前进;水有不同的折射率,所以光改变了前进方向。你以前听过这个,对吗?”
我点点头,“当然。”
“现在关于光所走路线有个有趣的性质。这条路线是这两点之间可能的最快的路线。”
“又来了?”
“想象一下,光线沿着这条路线前进。”他在图解中加了条虚线。
“这条假想中的路线比光实际走的路线要短。但是光在水中前进的速度比在空气中小,而这条假想的路线的很大一部分是在水中的,所以光沿着这条假想的路线所花的时间要比沿着实际路线要长。”
“好,我明白了。”
“现在想象一下,假设光沿和另一条路线前进。”他画了第二条虚线。
“这条路线减少了在水中的比例,但总长增加了。光沿着这条假想的路线所花的时间也要比沿着实际路线要长。”
Gary放下粉笔,用蘸着粉笔屑的手指指着黑板上的图解,“任何假想的路线都比实际的要花更多的时间。换一句话说,光线走的路线是最有可能走得走快的一条。这就是Fermat定理的最小时间原理。”
你发现Fermat原理有什么奇怪的地方了吗?你是不是感觉Fermat原理很诡异,但自己也说不清楚到底是为什么诡异?仔细想想你会发现,“最快到达”这种原理显然是不符合我们的行为方式的:假如我是光,我的传播规律是“最快到达”,但此时我要传播到哪里还不知道呢。Ted Chiang的小说对此也做出了详细的描述:
“然而我仍要问你关于Fermat定理的东西。它的一些东西让我感到奇怪,但我不能正确指出那是什么。它只是不像是物理法则。”
Gary的眼睛闪了一下,“我打赌我知道你想谈什么,”他用筷子把锅贴夹成两半,“你习惯于用起因和结果来思考折射:光照到水面上是起因,方向的变化是结果。但Fermat定理听上去很古怪,因为它以目的的形式来描述光的行为。它就像是光线的指挥官,‘你应该将抵达目的的时间最小化或最大化。’”
我想了一下,“继续说。”
“这是物理法则的一个老问题。人们在17世纪Fermat定理第一次成形时就一直在谈论它。Planck写了好几卷。本质是,普通的物理法则的表述是具有因果关系的,而像Fermat定理的可变法则具有目的性,几乎是目的论。”
“嗯,这样解释道挺有趣。让我想一下。”我拿起一支标签笔,在餐巾纸上画了幅图解,就是Gary在我的黑板上画的那幅,“好,”我想我很大声地说道,“那么让我们假设光的目的是要沿着最快的路线前进。这样的话,光如何走呢?”
“好吧,假若按人类行为学来说,光得检验每条可能的路线并计算每条得花多少时间。”他从盘子里戳起最后一块锅贴。
“那样做的话,”我继续道,“光线得知道目的在哪儿。假如目的地在某某其他地方,最快的路线就会不同。”
Gary再次点点头,“完全正确。‘最快的路线’的概念是无意义的,除非有特定的目的地。计算沿着一条假想的路线需多长时间也需要关于在这条路线上有什么东西的信息,比如水面在哪?”
我继续看着纸巾上的图解,“在光开始移动前,它得事先知道所有这一切,对吗?”
“这样说来,”Gary说,“光线不能沿着老路前进,然后再在后来返回。因为引起这样行为的路线不是最快的。在一开始光就已经做好了全部的计算。”
我心中暗想,在光线能够选择它移动的方向前,它已经知道它最终会在那里结束。我知道这让我想起了什么,我抬起头看着Gary,“这让我困扰。”
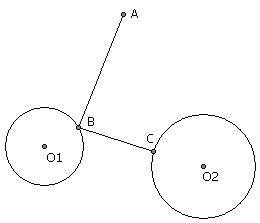
上面的论述似乎很抽象。我们来看一个实际的数学问题。这个问题有点怪,和其它的问题很不一样。给出一个点A,给出两个圆O1、O2,再给定O1上的一点B,问O2上是否存在一点C,使得B点的位置恰好能让AB+BC达到最小,也即对于O1上异于B的任一点B'都有AB'+B'C > AB+BC。你一时间可能找不到这个点C,这很正常,但光可以立即找到这个点C。因为从Fermat原理的角度看,光的思维方式是“逆向”的,这个别扭的题目正好顺应了它的思维方式。只要沿AB发射一条光线,在圆O1表面上发生反射后的光线与O2的交点即为点C。因为,A->B->C这条光路符合光的传播性质,这条路径是所有经过O1上一点到C的路径中最短的一条,其它所有的B'都会使光程增加。事实上,光就有这种神奇的本领:不管之前有过多少反射点,有过多少折射点,这条光线今后传播到的每一个点都满足这种无比别扭的“以它为终点则前面的定点均已达到最优”的性质。对于光来说,这是顺理成章的事;但从我们的角度来看,还没到目的地便能确保路径最优是很不可思议的。我们会习惯性地认为,光从A点出发往B走之前必须得先知道它的终点是C,然后才会知道B可以使光程最短,因此它才会往B走。这是明显有悖于我们熟知的因果关系的。或许说,这个世界本没有什么因果关系,仅仅是因为人类的思维被禁锢在了因果链式思维中?
接下来,我们举两个火星例子。两个都是经典的小学奥赛题。
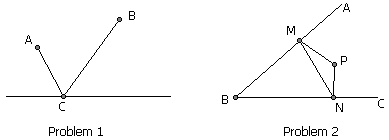
问题1:给定直线l同侧的两点A和B,在直线上找一点C使得折线ACB最短。
问题2:角ABC内有一点P,请在AB上找一点M,BC上找一点N,使得三角形PMN的周长最短。
类似的问题还有很多。很多这类几何极值问题都和Fermat原理有直接