这个月月初就开始看《从一到无穷大》,花了接近两个星期才看完。这确实是一本让人放不下手的好书。考虑到我的阅读速度,一个多星期一本书已经近乎神速了。在这本书里我经常会看到一些有趣的数学知识,前段时间我还写过书里提到的一个有趣的东西——环面上的染色问题反而比平面上的“四色问题”更加简单。这种例子并不罕见,很多时候一些扩展版的问题反而比原问题更加简单。在第八章,我看到了另一个好玩的东西:随机游走(random walk)问题。
随机游走问题是说,假如你每次随机选择一个方向迈出一个单位的长度,那么n次行动之后你离原点平均有多远(即离原点距离的期望值)。有趣的是,这个问题的二维情况反而比一维情况更加简单,关键就是一维情况下的绝对值符号无法打开来。先拿一维情况来说,多数人第一反应肯定是,平均距离应该是0,因为向左走和向右走的几率是一样的。确实,原点两边的情况是对称的,最终坐标的平均值应该是0才对;但我们这里考虑的是距离,它需要加上一个绝对值的符号,期望显然是一个比0大的数。如果我们做p次实验,那么我们要求的平均距离D就应该是
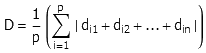
其中d的值随机取1或者-1。这里的绝对值符号是一个打不破的坚冰,它让处于不同绝对值符号内的d值无法互相抵消。但是,当同样的问题扩展到二维时,情况有了很大的改变。我们把每一步的路径投射到X轴和Y轴上,利用勾股定理我们可以求出离原点的距离的平方R^2的值:
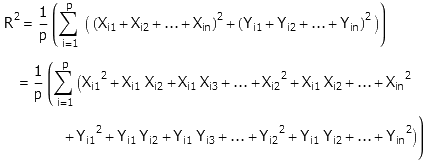
一旦把平方展开后,有趣的事情出现了:这些X值和Y值都是有正有负均匀分布的,因此当实验次数p充分大时,除了那几个平方项以外,其它的都抵消了。最后呢,式子就变成了
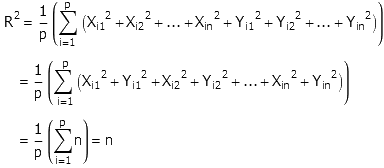
于是呢,就有平均距离R=sqrt(n) (准确的说是均方根距离)。我们得出,在二维平面内随机选择方向走一个单位的长度,则n步之后离出发点的平均距离为根号n。这是一个很美妙的结论。