昨天晚上躺在床上发呆，想了几则数学字谜。下面每个式子都对应一个英文单词，例如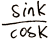
的意思就是tank。
你能猜出多少个来呢？
1. 
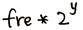
2. 
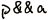
3. 
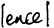
4. 
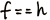
5. 
游戏
趣题：扫雷定理 互补棋盘上的数字和相等
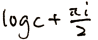
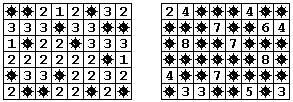
这是一个与扫雷游戏有关的非常好玩的问题。给定一个扫雷布局，定义它的“补集棋盘”为这样一个新布局，原来有雷的地方现在是空地，原来没有雷的地方现在都是雷。在棋盘的每块空地上都标有一个数字，它表示周围的8个方块中有多少颗雷。一个美妙的结论是，两个互补棋盘布局上的数字和是相等的。乍看之下似乎不可思议，但仔细一想便豁然开朗。你能想到这是为什么吗？
Cursor*10竟然出续集了！
学了拓扑学，我猛然领悟到了儿时游戏的真谛……
密码学协议举例（五）：两个人能够在电话上打牌吗？
密码学的应用范围非常广泛。每一样简单的社交活动里都有很大的学问。考虑这样一个问题，两个人想通过一部电话打牌，但他们都不信任对方。有没有可能仅通过一部电话实现扑克牌协议，并且保证游戏的公正性呢？
扑克牌的信息隐蔽性带来了很多与密码学协议相关的有趣问题。两个象棋大师可以在洗澡间一边冲澡一边大喊“炮八平五”、“马八进七”，一对围棋情侣可以在床上一边亲热一边呻吟“点三三”、“拆二”。等事情办完了，一盘精彩的棋局或许也就结束了。这些棋类游戏之所以可以“盲下”，就是因为在棋类游戏中，双方的局面信息都是完全公开的。不过，打牌就是另外一码事了。你说你出方片7，我怎么知道你有一个方片7？事先发牌？那谁来负责发牌呢？怎样发牌呢？难道我告诉你“发到你手中的是两张3一张5一张8一张9”？这样一看，两个人“盲打扑克牌”似乎是不可能的了，要么需要借助道具，要么需要第三者的帮助。不过，运用密码学知识，我们可以设计一套扑克牌协议，该协议能够实现随机的、隐蔽的、公平的发牌，并且不需要其它东西的帮助。我们以一手五张牌为例，说明如何实现“两人各摸五张牌”的程序。