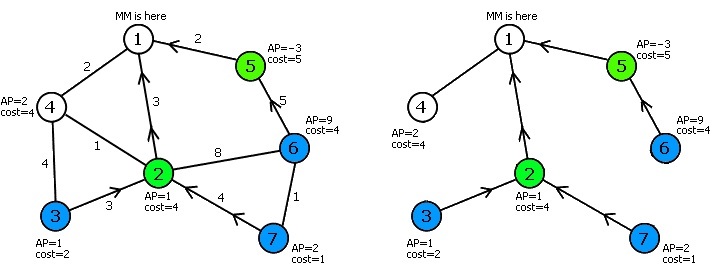
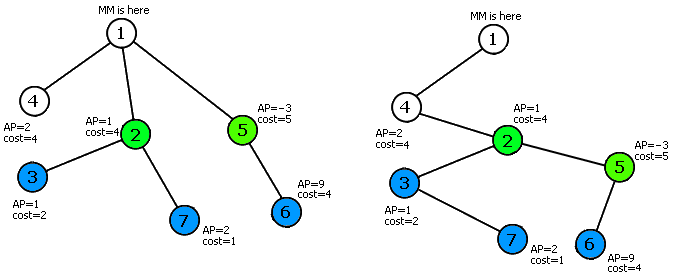
之所以没公布标程,是因为个人觉得标程写得比较丑。
既然有人需要就发布一下吧,标程丑总比没有标程好。
Problem 1
program whyleast;
procedure solve(t,a,b:integer);
begin
if t=0 then exit else
begin
solve(t-1,a,b);
writeln(a,' ',2);
solve(t-1,b,a);
writeln(2,' ',b);
solve(t-1,a,b);
end;
end;
{====main====}
var
n,i:integer;
ans:longint=1;
begin
assign(input,'whyleast.in');
reset(input);
assign(output,'whyleast.out');
rewrite(output);
readln(n);
for i:=1 to n do ans:=ans*3;
writeln(ans-1);
solve(n,1,3);
close(input);
close(output);
end.
Problem 2
program height;
const
OutputString:array[boolean]of string=('YES','NO');
type
rec1=record
h,p:longint;
end;
pointer=^rec2;
rec2=record
x,y:longint;
dir:boolean;
next:pointer;
end;
var
orderHeight : array[1..100000]of longint;
SortHeight : array[1..100000]of rec1;
Deg,DegHash : array[0..100000]of longint;
EdgeHash : array[1..100000]of pointer;
n,m,DegCount:longint;
procedure SwapRec(var t1,t2:rec1);
var
t3:rec1;
begin
t3:=t1;
t1:=t2;
t2:=t3;
end;
procedure SwapInt(var t1,t2:longint);
var
t3:longint;
begin
t3:=t1;
t1:=t2;
t2:=t3;
end;
function InsertEdgeHash(x,y:longint):integer;
var
newp:pointer;
begin
new(newp);
newp^.x:=x;
newp^.y:=y;
if orderHeight[x] > orderHeight[y] then
newp^.dir:=( 1.25*OrderHeight[y] <= orderHeight[x] )
else newp^.dir:=( 1.25*OrderHeight[x] > orderHeight[y] );
newp^.dir:=not newp^.dir;
newp^.next:=EdgeHash[x];
EdgeHash[x]:=newp;
exit( ord( newp^.dir ) );
end;
function FindEdgeHash(x,y:longint):integer;
{ -1: Not Found; 0: x-->y 1: x<--y
x Always Smaller than y }
var
now:pointer;
begin
now:=EdgeHash[x];
while now<>nil do
begin
if now^.y=y then
begin
now^.dir:=not now^.dir;
exit( ord( now^.dir ) );
end;
now:=now^.next;
end;
exit(-1);
end;
procedure UpdateDeg(t,c:longint);
begin
if deg[t]<>c then
begin
dec(DegHash[Deg[t]]);
if DegHash[Deg[t]]=0 then dec(DegCount);
inc(DegHash[c]);
if DegHash[c]=1 then inc(DegCount);
Deg[t]:=c;
end;
end;
procedure ReadHeight;
var
i:longint;
begin
readln(n,m);
for i:=1 to n do
begin
readln(OrderHeight[i]);
SortHeight[i].h:=OrderHeight[i];
SortHeight[i].p:=i;
end;
end;
procedure Sort(l,r:longint);
var
i,j,mid:longint;
begin
i:=l;
j:=r;
mid:=SortHeight[(i+j)div 2].h;
repeat
while SortHeight[i].h<mid do inc(i);
while SortHeight[j].h>mid do dec(j);
if i<=j then
begin
SwapRec(SortHeight[i],SortHeight[j]);
inc(i);
dec(j);
end;
until i>j;
if l<j then Sort(l,j);
if i<r then Sort(i,r);
end;
procedure Init;
var
low:longint=1;
high:longint=1;
i:longint;
begin
DegHash[0]:=n;
DegCount:=1;
for i:=1 to n do
begin
while SortHeight[low].h*1.25 < SortHeight[i].h do inc(low);
while ( high<n ) and ( SortHeight[i].h*1.25 >= SortHeight[high+1].h ) do inc(high);
UpdateDeg( SortHeight[i].p, high+low-i );
end;
end;
procedure Solve;
var
i,x,y:longint;
dir:integer;
newp:pointer;
begin
for i:=1 to m do
begin
readln(x,y);
if x>y then SwapInt(x,y);
dir:=FindEdgeHash(x,y);
if dir=-1 then dir:=InsertEdgeHash(x,y);
if dir=0 then SwapInt(x,y);
UpdateDeg(x,Deg[x]+1);
UpdateDeg(y,Deg[y]-1);
writeln( OutputString[DegCount=n] );
end;
end;
{====main====}
begin
assign(input,'height.in');
reset(input);
assign(output,'height.out');
rewrite(output);
ReadHeight;
Sort(1,n);
Init;
Solve;
close(input);
close(output);
end.
Problem 3
program wolf;
type
rec=record
left,right:integer;
end;
const
infinite=maxlongint div 3-100000;
//Make sure no overflows occur
var
k,n,m : integer;
map : array[1..1000,1..1000]of longint;
dist : array[1..1000]of longint;
hash : array[1..1000]of boolean;
father : array[1..1000]of longint;
; tree : array[1..1000]of rec;
attk : array[1..1000]of longint;
cost : array[1..1000]of integer;
minf : array[1..1000,0..100]of longint;
procedure readp;
var
i,x,y,d:longint;
begin
readln(k,n,m);
for i:=2 to n do
readln(attk[i],cost[i]);
for i:=1 to m do
begin
readln(x,y,d);
map[x,y]:=d;
map[y,x]:=d;
end;
end;
procedure init;
var
i,j:longint;
begin
for i:=2 to n do dist[i]:=infinite;
for i:=2 to n do hash[i]:=false;
dist[1]:=0;
hash[1]:=true;
for i:=1 to n do
for j:=1 to n do
if map[i,j]=0 then map[i,j]:=infinite;
for i:=1 to n do
for j:=1 to k do
minf[i,j]:=-infinite;
end;
procedure sssp;
var
i,j:longint;
min:longint=0;
minj:longint=1;
begin
for i:=1 to n-1 do
begin
for j:=1 to n do if not hash[j] then
begin
if ( min+map[minj,j] = dist[j] ) and ( father[j] > minj ) then
father[j]:=minj
else if min+map[minj,j] < dist[j] then
begin
dist[j]:=min + map[minj,j];
father[j]:=minj;
end;
end;
min:=infinite;
for j:=1 to n do if not hash[j] and (dist[j]<min) then
begin
minj:=j;
min:=dist[j];
end;
tree[ minj ].right:=tree[ father[minj] ].left;
tree[ father[minj] ].left:=minj;
hash[ minj ]:=true;
end;
end;
function solve(x,y:longint):longint; //(node,cost)
procedure update(var t1:longint;t2:longint);
begin
if t1<t2 then t1:=t2;
end;
var
ans:longint=-infinite;
i,t:longint;
begin
if minf[x,y]<>-infinite then exit(minf[x,y]);
if y>=cost[x] then ans:=attk[x];
if tree[x].left>0 then update(ans,solve(tree[x].left,y)+attk[x]);
if tree[x].right>0 then
begin
update(ans,solve(tree[x].right,y));
if y-cost[x]>0 then
update(ans,solve(tree[x].right,y-cost[x])+attk[x]);
end;
if (tree[x].left>0) and (tree[x].right>0) then
for i:=1 to y-1 do
update(ans,solve(tree[x].left,i)+solve(tree[x].right,y-i)+attk[x]);
minf[x,y]:=ans;
exit(minf[x,y]);
end;
procedure writep;
var
ans:longint=-infinite;
i,j:integer;
begin
for i:=0 to k do
if solve(1,i)>ans then ans:=solve(1,i);
writeln(ans);
{===For Debug===
for i:=1 to n do
begin
for j:=1 to k do write(minf[i,j]:3);
writeln;
end;
for i:=1 to n do writeln(tree[i].left,' ',tree[i].right);
}
end;
{====main====}
begin
assign(input,'wolf.in');
reset(input);
assign(output,'wolf.out');
rewrite(output);
readp;
init;
sssp;
writep;
close(input);
close(output);
end.
Problem 4
program garden;
const
dir:array[1..4,1..2]of integer=
((1,0),(0,1),(-1,0),(0,-1));
type
arr=array[1..10]of integer;
rec=record x,y:integer;end;
var
map:array[0..11,0..11]of boolean;
ans:array[1..100]of rec;
n,m,max:integer;
step:integer=1;
state:arr;
procedure readp;
var
i,j:integer;
ch:char;
begin
readln(m,n);
for i:=1 to n do
begin
for j:=1 to m do
begin
read(ch);
map[i,j]:=(ch='1');
inc(max,ord( map[i,j] ))
end;
readln;
end;
end;
procedure writep;
var
i:integer;
begin
for i:=1 to step do
writeln( '(' , ans[i].x , ',' , ans[i].y , ')' );
end;
procedure solve(x,y:integer);
var
tx,ty,d:integer;
step_cache:integer;
state_cache:arr;
begin
step_cache:=step;
state_cache:=state;
if step=max then
begin
writep;
exit;
end;
for d:=1 to 4 do
begin
tx:=x+dir[d,1];
ty:=y+dir[d,2];
while map[tx,ty] and ( not state[tx] and(1 shl (ty-1) )>0) do
begin
inc(step);
ans[step].x:=tx;
ans[step].y:=ty;
state[tx]:=state[tx] or ( 1 shl (ty-1) );
tx:=tx+dir[d,1];
ty:=ty+dir[d,2];
end;
tx:=tx-dir[d,1];
ty:=ty-dir[d,2];
if (tx<>x) or (ty<>y) then solve(tx,ty);
state:=state_cache;
step:=step_cache;
end;
end;
{====main====}
var
i,j:integer;
begin
assign(input,'garden.in');
reset(input);
assign(output,'garden.o
ut');
rewrite(output);
readp;
for i:=1 to n do
for j:=1 to m do
if map[i,j] then
begin
ans[1].x:=i;
ans[1].y:=j;
state[i]:=1 shl (j-1);
solve(i,j);
state[i]:=0;
end;
close(input);
close(output);
end.
依然欢迎大家来挑错