题目在这里:http://www.matrix67.com/blog/article.asp?id=241
如果机房马上要关门了,或者你急着要和MM约会,请看简要题解:
1. 用类似于传统hanoi的递归方法可以做到3^n-1次。这显然是最多的了,因为总的状态数也只有3^n个。
2. 可以证明,竞赛图中不存在环当且仅当所有顶点的出度从小到大排列依次为0, 1, 2, … , n-1 。
3. 在最短路树上做树状DP,需要多叉转二叉。注意几种需要输出0的情况。
4. 搜索,算是练基本功了。用位运算优化,不加任何剪枝就能过。
否则,请慢慢阅读——
Problem 1: 为什么最少
如果你还不熟悉Hanoi塔的解法,去题目中提到的那篇日志看看吧。如果你已经熟悉Hanoi塔的解法,你会立刻想到这道题的解法:依然是递归地解决。至于怎么递归,样例已经告诉我们了:把前n-1个金片从1号柱搬到3号柱,把第n片移到2号柱,又把那n-1片从3号柱搬回1号柱,再把第n片搬到3号柱,最后把那n-1个金片又搬过来,完成整个操作。
我们下面解决三个问题:为什么这样不会重复出现状态,这样的移动步数是多少,为什么这样的操作步数是最多的。
为什么这样不会出现重复的状态呢?因为我们假设前n-1个金片的移动过程中没有重复状态,而三次对n-1的调用时整个状态由于第n个金片的位置不同而不同。
这样的方法获得的操作步数是多少呢?答案是3^n-1。我们可以用数学归纳法证明,n=1时步数为2显然正确,而f(n+1)=3f(n)+2=3*(3^n-1)+2=3^(n+1)-1。
为什么这样的操作步数是最多的呢?废话,这样的操作步数当然是最多的,因为总的状态数也只有3^n个(每个金片的三种可能的位置确定了一种状态),你的移动步骤能比这个数目还多就见鬼了。
这道题有人用了math库,没有提供math库导致无法编译是我的失误,向大家道歉。
Hanoi问题的变种太多了,比如多根柱子、单向移动、双色金片等等。dd上次不是也出了一题么。
这题代码很短,我公布在下面。program whyleast;
procedure solve(t,a,b:integer);
begin
if t=0 then exit else
begin
solve(t-1,a,b);
writeln(a,' ',2);
solve(t-1,b,a);
writeln(2,' ',b);
solve(t-1,a,b);
end;
end;
{====main====}
var
n,i:integer;
ans:longint=1;
begin
assign(input,'whyleast.in');
reset(input);
assign(output,'whyleast.out');
rewrite(output);
readln(n);
for i:=1 to n do ans:=ans*3;
writeln(ans-1);
solve(n,1,3);
close(input);
close(output);
end.
Problem 2: 身高控制计划
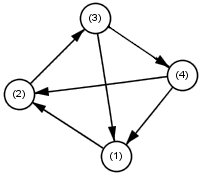
一个竞赛图是指任两个点之间都有一条有向边的图。竞赛图有很多奇妙的性质,比如一个竞赛图必然存在一条经过所有节点的路等等。
下面我们证明,竞赛图中不存在环当且仅当所有顶点的出度从小到大排列依次为0, 1, 2, … , n-1 :
如果一个有向图的所有点出度都至少为1,那么这个图一定有环,因为在找到环之前DFS总可以找到新的节点。如果有向图无环,必然存在一个点没有出度。由于任两点之间都有有向边,那么其它所有点都要连一条边指向它,这样其它所有点的出度都至少为1了。删掉这个出度为0的点后剩下的图仍然无环,不断对剩下的图继续上面的过程就得到了我们的结论。
现在我们的算法就很明确了,首先统计初始状态下的出度,然后设计某种数据结构完成两种操作:改变一个数(加一减一),询问所有数是否恰好为0, 1, 2, … , n-1 。
统计初始状态下的出度方法有很多,这里介绍两个。首先对身高排序,然后对于每个人进行二分,寻找有序数列中该数的4/5和5/4各在什么地方。还有一种方法也是先排序,然后从左到右扫描整个序列,并保持两个指针始终指向4/5和5/4处。每次开始处理一个新的数时都把两个指针适当地右移直到超出了这个数的4/5或5/4为止。两种方法都是O(nlogn)。别以为第二种方法是线性的哦,线性算法之前还有一个排序呢。
操作的处理也有不少方法。最简单的方法就是统计当前图中出度的数目有多少种。就是说,用a[i]表示出度为i的点有多少个,然后不断更新a[i]>0的有多少个。当这个数目等于n时我们就认为图中没有环(因为出度可能的取值只有从0到n-1共n种)。
注意,由于同一条边可能被操作多次,因此需要一个Hash表(开散列)来判重。具体地说,你需要判断这条边以前被操作过奇数次还是偶数次,以决定哪边的出度要增加,哪边的出度要减小。
Problem 3: 狼的复仇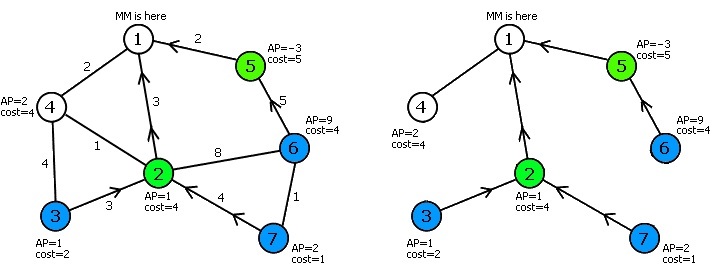
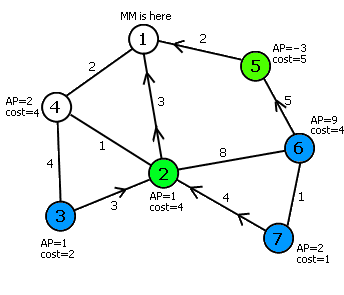
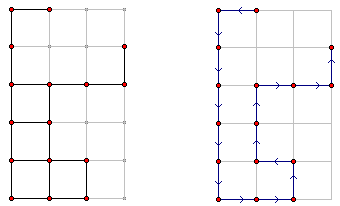
把这个问题中所有的最短路都画出来是什么样子?它一定是一棵树!为什么?首先,图肯定是连通的,因为源点到任一个点都有一条最短路;其次,图肯定无环,因为源点到任一个点只有一条最短路(环的出现将意味着某些点有更短的路存在)。仔细想一下Dijkstra的算法过程,不难想到Dijkstra算法的实质就是在建这棵树——每一次由x节点加上边x-y扩展到y节点就记作x是y的父亲。注意观察上图中左图是如何变成右图的。这样,题目变成了这种形式:在有根树上,除根节点之外的其它节点中选择一些节点,使得这些节点和它们所有祖先的权值和最大。这是一个经典的树型动态规划模型。我们用f[i,j]表示以节点i为根节点的子树花费j个单位的材料最多可以得到多大的攻击力。令节点1的材料和攻击力都为0,那么最后输出f[1,0..k]中的最大值即可。决策分为两类,要么该位置建一个塔,要么把所有材料适当地分给儿子(自己就不需要再建了)。但这样的复杂度太高,我们需要用DP嵌套或者更巧妙的多叉转二叉来解决。
DP嵌套理解起来更简单,它主要是解决这样一个子问题:若某个节点有m个儿子,我们需要寻找当j1+j2+…+jm等于某个定值时f[儿子1,j1]+f[儿子2,j2]+…+f[儿子m,jm]的最大值。这个子问题与我的某次模拟赛中论文课题选择那道DP题几乎是一模一样,看一看那道题就明白了。下面简单描述多叉转二叉的方法。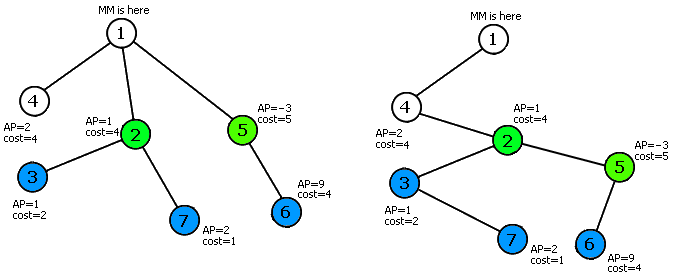
如果你还不知道多叉转二叉的话,这道题是一个绝好的学习材料。一棵多叉树可以用“左儿子右兄弟”的方法转为二叉树,具体的说就是把多叉树转化为这种形式:节点的左儿子才是真正的儿子,节点的右儿子只是和它同辈的兄弟。注意看上图的左图是如何变成右图的。现在,我们的f[i,j]表示