考虑一个事件，它有两种概率均等的结果。比如掷硬币，出现正面和反面的机会是相等的。现在我们希望知道，如果我不断抛掷硬币，需要多长时间才能得到一个特定的序列。
序列一：反面、正面、反面
序列二：反面、正面、正面
首先，我反复抛掷硬币，直到最近的三次抛掷结果形成序列一，然后我记下这次我抛掷了多少次才得到了我要的序列。重复执行这个过程，我可以算出得到序列一平均需要的抛掷次数。同样地，反复抛掷硬币直到序列二产生，它所需要的次数也有一个平均值。你认为这两个平均值哪一个大哪一个小？换句话说，出现序列一平均所需的抛掷次数少还是出现序列二平均需要的次数少？
大多数人会认为，两个序列会以同样快的速度出现，因为在所有“正”和“反”的8种三元组合里，“反正反”和“反正正”各占1/8，其概率是均等的。而事实上，我们将会看到掷出序列二所需的次数更少一些。不妨考虑这样一个问题：在由“正”和“反”构成的n位01序列中，有多少个序列以序列一结尾但之前不曾出现过序列一？有多少个序列以序列二结尾但之前不曾出现过序列二？当n比较小时，两者答案是一样的（例如n=3时符合要求的情况都是唯一的），但到后来n越大时，两者的差距越明显：后者的个数总比前者的个数要多一些。不妨看一看n=6的情况。对于序列一，只有以下5个序列是符合要求的：
- 反反反反正反
- 反正正反正反
- 正正正反正反
- 正反反反正反
- 正正反反正反
但对于序列二来说，符合条件的序列就有7个：
- 反反反反正正
- 反正反反正正
- 反反正反正正
- 正反反反正正
- 正正反反正正
- 正正正反正正
- 正反正反正正
你可以通过计算机编程枚举，计算一下n为其它值的情况。计算结果和刚才也一样：在n位01序列中，以序列二结尾但之前不含序列二的情况不会少于以序列一结尾但之前不含序列一的情况。这说明，抛掷第n次硬币后恰好出现了序列二，其概率不会小于恰好出现序列一的概率。显然，当n渐渐增大时，这个概率应该呈下降趋势；同时，随着n的增长，两个序列各自出现的概率由相等开始慢慢拉开差距，第n次抛掷产生序列二的概率下降得要缓慢一些，或者说更多的情况集中发生在n更小的时候。因此总的来说，出现序列二所需要的抛掷硬币次数的期望值更小。
虽然我们通过一系列的观察验证了这个结论，并且我们也相信这个结论是正确的（虽然没有严格的证明），但我们仍然不是很接受这个结论。这种情况是有悖于我们的直觉的，它与我们的生活经验不相符合。此刻，我们迫切需要一个解释，来说明这种出人意料的反常现象产生的原因。
如果不亲自做几次试验的话，你很难体会到这种微妙的差距。考虑整个游戏的实际过程，“反正正”序列显然会出现得更早一些。假如某一次我们得到了序列“反正”。如果我们需要的是“反正反”序列，那么下一次抛掷结果为反面将结束本轮的抛掷，而下一次是正面则前功尽弃，你必须再次从零开始。如果我们需要的是“反正正”序列，那么下一次抛掷结果为正面将结束本轮的抛掷，而下一次是反面的话我至少不会惨到一切归零，这相当于我已经有了一个反面作为新的开头，只需再来两个正面即可。这样看的话，提前掷出“反正正”的可能性更大一些。
反复体会上面的想法，了解KMP算法的网友会恍然大悟：这就是KMP算法的基本思路！考虑这样一个问题：我们在当前字串中寻找子串“反正正”第一次出现的位置。假如当前已经能匹配模式串的前两个字“反正”，主串中的下一个字是“正”则匹配成功，主串的下一个字是“反”则将使模式串的当前匹配位置退到第一个字。考虑一个更复杂的例子：我们希望在主串中寻找子串abbaba，现在已经在主串中找到了abbab。如果主串下一个字符是a，则成功匹配；如果主串下一个字符是b，则模式串最多能匹配到的位置退到了第三个字符，我只需要从abb开始继续匹配，而不必一切从头再来。
我们可以用KMP算法完美地解决上面的问题。首先预处理出一个数组c，c[i,0]表示模式串匹配到了第i个字符，主串下一个字符为0（反）时，模式串的匹配位置将退到哪里；同样地，c[i,1]表示模式串匹配到了第i个字符，主串下一个字符为1（正）时，新的模式串匹配位置在什么地方。设f[i,j]表示第i次抛掷硬币后恰好匹配到模式串第j位有多少种情况，则f[i,j]=Σf(i-1,k) + Σf(i-1,l)，其中k满足c[k,0]=j，l满足c[l,1]=j。将f[i,j]除以2的i次方，我们就得到了相应的概率值。或者更直接地，设P[i,j]表示第i次抛掷硬币后，最远能匹配到的模式串位置是第j位的概率，则P[i,j]=Σ( P(i-1,k)/2 ) + Σ( P(i-1,l)/2 )。注意，我们还应该添加一种特殊的概率值P[i,*]，它表示在主串第i个字符以前已经成功匹配过的概率，这样的话下表中每一列的和才能为1。
来看一看程序的输出结果：
Pattern 1: s[]="aba"
主串位置 1 2 3 4 5 6 7 8 9 10
匹配到s[0] 0.5000 0.2500 0.2500 0.2500 0.2188 0.1875 0.1641 0.1445 0.1270 0.1113
匹配到s[1] 0.5000 0.5000 0.3750 0.3125 0.2813 0.2500 0.2188 0.1914 0.1680 0.1475
匹配到s[2] 0.0000 0.2500 0.2500 0.1875 0.1563 0.1406 0.1250 0.1094 0.0957 0.0840
匹配到s[3] 0.0000 0.0000 0.1250 0.1250 0.0938 0.0781 0.0703 0.0625 0.0547 0.0479
已找到匹配 0.0000 0.0000 0.0000 0.1250 0.2500 0.3438 0.4219 0.4922 0.5547 0.6094
Pattern 2: s[]="abb"
主串位置 1 2 3 4 5 6 7 8 9 10
匹配到s[0] 0.5000 0.2500 0.1250 0.0625 0.0313 0.0156 0.0078 0.
0039 0.0020 0.0010
匹配到s[1] 0.5000 0.5000 0.5000 0.4375 0.3750 0.3125 0.2578 0.2109 0.1719 0.1396
匹配到s[2] 0.0000 0.2500 0.2500 0.2500 0.2188 0.1875 0.1563 0.1289 0.1055 0.0859
匹配到s[3] 0.0000 0.0000 0.1250 0.1250 0.1250 0.1094 0.0938 0.0781 0.0645 0.0527
已找到匹配 0.0000 0.0000 0.0000 0.1250 0.2500 0.3750 0.4844 0.5781 0.6563 0.7207
这下我们可以清楚地看到，序列二提前出现的概率要大得多。注意到，根据我们的概率定义，表格中每一列的数字之和都是1。同时，倒数第二行的数字之和（有无穷多项）也应该为1，因为最后一行的概率就是倒数第二行的概率值累加的结果，而根据最后一行概率的定义，主串无穷长时已找到匹配的概率应该为1。因此，我们也可以把倒数第二行看作是模式串在主串第i个位置首次匹配成功的概率。我们可以根据这一结果近似地计算出抛掷次数的期望值。
Matrix67原创
转贴请注明出处
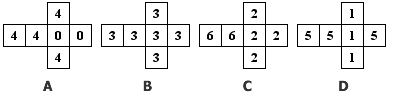在数学中，比较运算是有传递性的。如果A>B，且B>C，那么一定有A>C。但现实生活中却不一定是这样。三个人两两之间进行比赛，有可能A比B要强，B比C要强，但C反过来赢了A。事实上，这种现象即使在数学中也是存在的。在一些概率事件中，类似的“大小关系”很可能并不满足传递性。