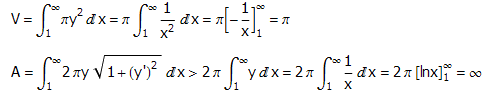看到新词就上一下Wikipedia确实是一个好习惯。前一篇日志的那个pdf里作者提到了Gedankenexperiment(Thought experiment)，上Wikipedia一查果然学到了牛B的新东西。好多物理定律其实完全是由思维实验推导出来的，难以置信仅仅是思考竟然就能得出物理世界遵从的各种法则。经典的物理思维实验有Newton大炮、Galileo斜塔实验、Schrödinger的猫猫、Maxwell的妖怪等等。还有，Turing机也是一个伟大的思维实验。

   
    数学上的不少悖论（特别是涉及到维度和无穷的悖论）都是相当有趣的思维实验。Gabriel喇叭是y=1/x在[1,+∞)上的图象沿x轴旋转一周所形成的旋转体。这个简单的三维图形有一个奇特的性质：它的表面积无穷大，却只有有限的体积。为了证实这一点，只需注意到：
   
    Gabriel喇叭会导出一个非常诡异的悖论：如果你想用涂料把Gabriel喇叭的表面刷一遍，你需要无穷多的涂料；然而把涂料倒进Gabriel喇叭填满整个内部空间，所需要的涂料反而是有限的。
    有网友一定会问，那有没有什么二维图形，面积有限大，周长却无限长呢？答案是肯定的，Koch雪花就是这样一个经典的例子。不过，通过分形构造出来的这类图形似乎并不存在涂料悖论，因为递归到一定深度时分形图形的尺度将小于表面涂料的厚度，因此表面大小不能永无止境地算下去，涂满表面所需的涂料不再是无穷多。当考虑到涂料厚度时，原先的悖论也可以解释清楚了：填充内部空间仅仅涂满了图形的内表面，一旦考虑到涂料的厚度，它和外表面的区别就出来了。

Read more…

    我在学校时，时不时会有人闯进宿舍，给宿舍里的每个人发一张调查表邀请大家填写。如果我不是很忙的话，通常还是很乐意填写的。不过，有时我很悲哀的发现，很多调查表的设计都很缺乏科学性。设计一张合理的调查表并不是一件容易的事情，你需要综合考虑各方面的因素。例如，假如你需要在调查表中问一个极度隐私的问题，尽管你在调查表上再三强调你们的保密措施，但你真的指望所有人都能够如实地回答吗？你真的指望会有人在“我不是处男/处女”或“我有同性恋倾向”前面打一个勾然后把表递到问卷回收人的手中吗？
    让我们考虑这样一个问题：你希望在调查表上问一个隐私问题。为了方便起见，假设这个问题只有“是”和“否”两个选项。有什么方案能够绝对地保证个人隐私完全不可能被泄露，让每个人都能够放心地填写，并且问卷回收之后能够得到一个准确的统计结果？
Read more…

    在这篇文章里，我们从信息论的角度证明了，基于比较的排序算法需要的比较次数（在最坏情况下）至少为log2(n!)，而log(n!)=Θ(nlogn)，这给出了比较排序的一个下界。但那里我们讨论的只是最理想的情况。一个事件本身所含的信息量是有大小之分的。看到这篇文章之后，我的思路突然开阔了不少：信息论是非常强大的，它并不只是一个用来分析理论最优决策的工具。从信息论的角度来分析算法效率是一件很有趣的事，它给我们分析排序算法带来了一种新的思路。

    假如你手里有一枚硬币。你希望通过抛掷硬币的方法来决定今天晚上干什么，正面上网反面看电影。投掷硬币所产生的结果将给你带来一些“信息”，这些信息的多少就叫做“信息量”。如果这个硬币是“公正”的，正面和反面出现的概率一样，那么投掷硬币后不管结果咋样，你都获得了1 bit的信息量。如果你事先就已经知道这个硬币并不是均匀的，比如出现正面的概率本来就要大得多，这时我们就说事件结果的不确定性比刚才更小。如果投掷出来你发现硬币果然是正面朝上，这时你得到的信息量就相对更小（小于1 bit）；反之如果投掷出来居然反面朝上了，那你就得到了一个相对较大的信息量（大于1 bit）。但平均下来，我们得到的信息量是小于1 bit的，因为前者发生的可能性毕竟要大一些。最极端的情况就是，这是一枚被捣了鬼的魔术硬币，你怎么投都是正面。此时，你投了硬币等于没投，反正结果都是正面朝上，你得到的信息量永远为0。
    这个理论是很符合生活实际的。昨天晚上我出去吃饭时，坐在我后面的那个人是男的还是女的？这种问题就比较有价值，因为大家都猜不到答案究竟是什么；但要问我昨天跟谁一起出去上自习去了，问题的答案所含的信息量就变小了，因为大家都知道如果我破天荒地跑去自习了的话多半是有MM陪着一起去的。如果有网友问我是男的还是女的，那就更不可思议了，因为我不但多次在这个Blog里提到我一直想找一个合适的MM，还在AboutMe里面发了我的照片。如果某人刚操完一个MM，突然扭过头去问“对了，你是男的还是女的呀”，那这个人绝对是一个不折不扣的大傻B，因为这个问题所能带来的信息量几乎为0。
    总之，当每种结果出现的概率都相等，事件的不确定性达到最大，其结果最难预测时，事件的发生将会给我们带来最大的信息量。我们把一个事件的不确定程度叫做“熵”，熵越大表明这个事件的结果越难以预测，同时事件的发生将给我们带来越多的信息。如果在排序算法里每次比较的熵都是最大的，理论上来说这种（基于比较的）排序算法就应当是最优的。但我们一会儿将看到，我们已知的排序算法总是不完美的，每种算法都会或多或少地存在一些价值明显不大的比较。

Read more…

1. Goldbach猜想是说，任一大于等于4的偶数一定能表示成两个质数之和。关于质数，我们还有这样一个有趣的结论：对于任何整数n>1，存在质数p满足n<=p<2n。这个结论对Goldbach猜想是很“有利”的，因为它是Goldbach猜想的一个必要条件。倘若对于某个正整数n，n和2n之间没有质数，那么偶数2n就不能表示为两个质数之和了，因为所有可以用的质数都比n小，再怎么也加不出2n来。注意，如果这个结论错了，猜想也就被推翻了；但如果这个结论对了，猜想也不一定是对的。但即使这样，我们仍然习惯性地认为，验证了推论的正确性后猜想的可靠程度也或多或少的有了些提高，换句话说猜想为真的可能性更大了。这种思维合理吗？

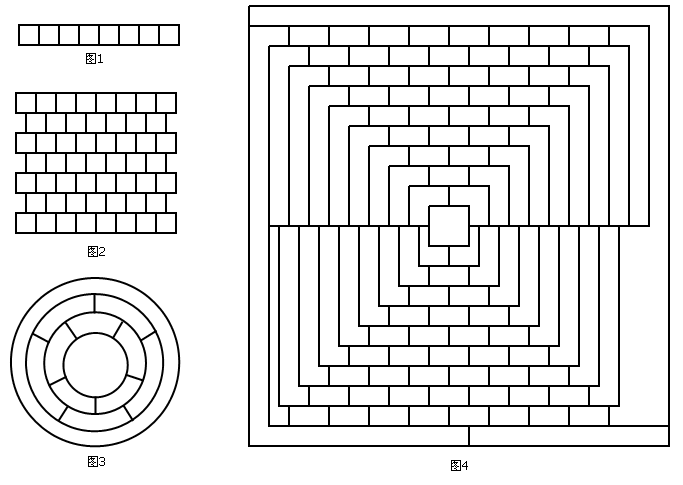
2. 长期以来，人们都在思考：对任一给定的平面图进行染色，要想使得有公共边的区域颜色不同，最少需要多少种颜色。四色猜想（现在已经是四色定理了）认为，只需要最多四种不同的颜色就足够了。我们可以随便画一些图进行验证，每一次检验后我们都会或多或少地更加相信结论的正确性。你可以尝试寻找下面的图1、图2和图3的合法解，检验一下猜想是否正确。验证哪一个图更有价值？你或许会这样回答：验证第一个图毫无价值，因为它显然有可行的染色方案；验证第三个图最有价值，因为它看上去最像反例，证实了它确实有解后，你会更加坚信四色猜想的正确性。1975年的4月1日，杂志Scientific American的数学专栏作家Martin Gardner宣布他找到了一个四色猜想的反例（图4）。当然，这只是一个愚人节的笑话。寻找图4的解非常困难，以致于看上去几乎是不可能的。一旦你成功找出了图4的解，对四色猜想的信任程度可就不只提高一点点了。“对猜想的某个结论进行验证，结论越是不可思议，证实以后原猜想的可靠程度就提高得越多”，这种思维是合理的吗？
  

  
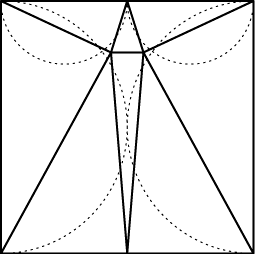
3. 你认为，是否有可能把一个直角三角形分成若干个锐角三角形？你很可能花了一节古代汉语课的时间苦思冥想，结果直角三角形没搞出来，倒是碰巧把一个正方形分成了8个锐角三角形。虽然你仍不知道一个直角三角形是否能分成若干个锐角三角形，但你找到了一个正方形的解，你会强烈地感觉到直角三角形也是有解的。这是什么原因呢？注意到，如果三角形能分的话正方形一定能分，但反过来却不一定。不过，这里面还有一些更微妙的关系：我们倾向于相信如果连直角三角形都没法分，正方形应该更没法分了。既然现在正方形已经解决了，那三角形也就快了。“B是A的结论，且没有A的B很不可靠，则证实了B可以极大地提高A的可信度”，这种思维合理吗？

4. 关于“如果他错了，那我对的概率就更大了”的思维。A、B两人被一个实际问题难住了，双方就问题中的两个变量的变化关系争执不休。A认为，函数图像画出来应该是一个开口朝上的二次函数；B则认为，函数图像应该是一个正弦函数。注意到一个有趣的事实：这两种猜测满足矛盾率，但不满足排中率。就是说，有可能A和B都错了，但是A和B不可能都对。紧接着他们发现，这个函数存在至少一个极大值，A的猜测显然是错的。虽然这并不能表明B的猜测就是对的，但我们能不能说B猜对的概率变大了？

    下面的内容是G.Pólya的Mathematics and Plausible Reasoning Vol 2里的精华：用概率来分析合情推理模式。我们可以用概率知识来描述上面这些合乎情理的推测。如果你还不知道什么叫做条件概率，建议你先看一看这篇文章。
    注意到P(A)*P(B|A)永远等于P(B)*P(A|B)，它们都等于P(A∩B)。如果B是A的一个推论，那么有P(B|A)=1（若A为真则B必为真）。于是我们有P(A)=P(B)*P(A|B)。这里，P(A|B)有一个形象的意义：结论B的证实可以使我们对A的信任改变多少。假如P(A|B)不变，则如果等式右边的P(B)增加了，P(A)也会增加。这也就说明了我们的第一个合情推理模式：对猜想的一个结论更加信任，对猜想本身也更加信任。
    这个式子还能告诉我们更多的东西。把P(B)除过去，我们有P(A|B)=P(A)/P(B)，其中等式左边的P(A|B)表示的仍然是证实了B以后A为真的概率，也就是验证B结论的价值。我们很清楚地看到，P(B)处于分母的位置。那么，结论B本身为真的概率越小，证实了B后对A的影响也就越大。
    注意P(B)=P(A∩B)+P(～A∩B)=P(A)*P(B|A)+P(～A)*P(B|～A)，而B是A的一个结论，即P(B|A)=1。于是，等号右边变为P(A)+[1-P(A)]*P(B|～A)。利用前面的结论，我们用P(A)/P(A|B)代替等式左边的P(B)，则有P(A|B)=P(A)/[P(A)+[1-P(A)]*P(B|～A)]。可以看到，如果P(B|～A)越小，则P(A|B)越大。这就是说，在没有A的前提下B成立可能性越小，证实了B之后A为真的可能性就越大。
    最后，我们看一看A和B不相容的情况。此时，P(A∩B)=0，于是
P(A) = P(A∩B) + P(A∩～B)
      = P(A∩～B)
      = P(～B) * P(A|～B)
      = [1-P(B)] * P(A|～B)
    把1-P(B)除过去，就有P(A|～B)=P(A)/[1-P(B)]，显然P(A|～B)是大于P(A)的，也即排除了B的猜测后A对的可能性比原来更高了。我们还可以清楚地看到，如果我们之前越相信B，则B被驳倒后A正确的可能性提高得就越多。