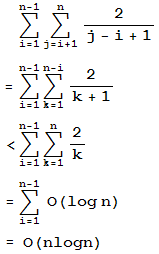在每一代的繁殖中，单个的阿米巴原虫有3/4的概率分裂成两个，有1/4的概率死亡（而不产生下一代）。初始时只有一个阿米巴原虫，求阿米巴原虫会无限繁殖下去的概率。
    答案在下面。

    解答：令p为单个阿米巴原虫分裂的概率（题目中等于3/4），令P为我们要求的概率（无限繁殖的概率）。
    初始时的那个阿米巴原虫有p的概率分裂为两个，至少有一个可以无限生存下去的概率为1-(1-P)^2。那么，我们得到式子：
      P = p*( 1 – (1-P)^2 )

    化简后得到：
      p*P^2 + (1 – 2p)P = 0

    或者写成：
      P * ( pP + ( 1-2p ) ) = 0

    由于P≠0，因此pP+(1-2p) = 0，即P = (2p-1)/p

    可以看到，如果一个阿米巴原虫分裂的概率没超过1/2，那么它不可能永远生存下去无限生存下去的概率为0。在我们的题目中，p=3/4，因此阿米巴原虫无限繁殖的概率为2/3。

    不知道大家见过没有，我今天偶然看到，在这里写一下。
    箱子里有两个信封：“一个信封里有1元钱，另一个有10元”有1/2的概率；“一个信封里有10元钱，另一个有100元”有1/4的概率；“一个信封里有100元钱，另一个有1000元”有1/8的概率……也就是说，有1/2^n的概率发生这样的事情，一个信封里有10^(n-1)元钱，另一个信封里有10^n元钱。现在你拿到一个信封，看到了里面有x元钱。给你一次机会换成另外那个信封，问你换不换。
    举个例子，假如我们拿到了100元钱的信封，那么换一个信封得到1000元的概率是得到10元的概率的一半。也就是说，如果我们拿到了x元钱，换一个信封的话有1/3的概率多得9x元，有2/3的概率失去0.9x元。它的期望值是增加2.4x元，这告诉了我们换一个信封显然更好。
    现在的问题是，既然总是换个信封好些，那么为什么我们不一开始就选择另外那个信封呢？

大家可以在下面讨论
我就不参与讨论了，虽然我也不知道是怎么回事

    这个问题让我想到了Newcomb悖论，说有个妖精可以预言你将拿一个箱子还是两个箱子，大家一定见过。

    A highly superior being from another part of the galaxy presents you with two boxes, one open and one closed. In the open box there is a thousand-dollar bill. In the closed box there is either one million dollars or there is nothing. You are to choose between taking both boxes or taking the closed box only. But there's a catch.
    The being claims that he is able to predict what any human being will decide to do. If he predicted you would take only the closed box, then he placed a million dollars in it. But if he predicted you would take both boxes, he left the closed box empty. Furthermore, he has run this experiment with 999 people before, and has been right every time.
    What do you do?
    On the one hand, the evidence is fairly obvious that if you choose to take only the closed box you will get one million dollars, whereas if you take both boxes you get only a measly thousand. You'd be stupid to take both boxes.
    On the other hand, at the time you make your decision, the closed box already is empty or else contains a million dollars. Either way, if you take both boxes you get a thousand dollars more than if you take the closed box only.

    Newcomb悖论是很荒唐的，很不具有数学的科学性。但这篇日志介绍的悖论在科学性上是可以承认的。

    本文被华丽的分割线分为了四段。对于O(nlogn)的排序算法，我们详细介绍归并排序并证明归并排序的时间复杂度，然后简单介绍堆排序，之后给出快速排序的基本思想和复杂度证明。最后我们将证明，O(nlogn)在理论上已经达到了最优。学过OI的人一般都学过这些很基础的东西，大多数OIer们不必看了。为了保持系列文章的完整性，我还是花时间写了一下。

    首先考虑一个简单的问题：如何在线性的时间内将两个有序队列合并为一个有序队列（并输出）？

A队列：1 3 5 7 9
B队列：1 2 7 8 9

    看上面的例子，AB两个序列都是已经有序的了。在给出数据已经有序的情况下，我们会发现很多神奇的事，比如，我们将要输出的第一个数一定来自于这两个序列各自最前面的那个数。两个数都是1，那么我们随便取出一个（比如A队列的那个1）并输出：

A队列：1 3 5 7 9
B队列：1 2 7 8 9
输出：1

    注意，我们取出了一个数，在原数列中删除这个数。删除操作是通过移动队首指针实现的，否则复杂度就高了。
    现在，A队列打头的数变成3了，B队列的队首仍然是1。此时，我们再比较3和1哪个大并输出小的那个数：

A队列：1 3 5 7 9
B队列：1 2 7 8 9
输出：1 1

    接下来的几步如下：

A队列：1 3 5 7 9         A队列：1 3 5 7 9         A队列：1 3 5 7 9          A队列：1 3 5 7 9
B队列：1 2 7 8 9   ==>   B队列：1 2 7 8 9   ==>   B队列：1 2 7 8 9    ==>   B队列：1 2 7 8 9     ……
输出：1 1 2              输出：1 1 2 3            输出：1 1 2 3 5           输出：1 1 2 3 5 7

    我希望你明白了这是怎么做的。这个做法显然是正确的，复杂度显然是线性。

    归并排序(Merge Sort)将会用到上面所说的合并操作。给出一个数列，归并排序利用合并操作在O(nlogn)的时间内将数列从小到大排序。归并排序用的是分治(Divide and Conquer)的思想。首先我们把给出的数列平分为左右两段，然后对两段数列分别进行排序，最后用刚才的合并算法把这两段（已经排过序的）数列合并为一个数列。有人会问“对左右两段数列分别排序时用的什么排序”么？答案是：用归并排序。也就是说，我们递归地把每一段数列又分成两段进行上述操作。你不需要关心实际上是怎么操作的，我们的程序代码将递归调用该过程直到数列不能再分（只有一个数）为止。
    初看这个算法时有人会误以为时间复杂度相当高。我们下面给出的一个图将用非递归的眼光来看归并排序的实际操作过程，供大家参考。我们可以借助这个图证明，归并排序算法的时间复杂度为O(nlogn)。

[3] [1] [4] [1] [5] [9] [2] [7]
  \ /     \ /     \ /     \ /
[1 3]   [1 4]   [5 9]   [2 7]
     \   /           \   /
   [1 1 3 4]       [2 5 7 9]
           \       /
       [1 1 2 3 4 5 7 9]

    上图中的每一个“ \ / ”表示的是上文所述的线性时间合并操作。上图用了4行来图解归并排序。如果有n个数，表示成上图显然需要O(logn)行。每一行的合并操作复杂度总和都是O(n)，那么logn行的总复杂度为O(nlogn)。这相当于用递归树的方法对归并排序的复杂度进行了分析。假设，归并排序的复杂度为T(n)，T(n)由两个T(n/2)和一个关于n的线性时间组成，那么T(n)=2*T(n/2)+O(n)。不断展开这个式子我们可以同样可以得到T(n)=O(nlogn)的结论，你可以自己试试。如果你能在线性的时间里把分别计算出的两组不同数据的结果合并在一起，根据T(n)=2*T(n/2)+O(n)=O(nlogn)，那么我们就可以构造O(nlogn)的分治算法。这个结论后面经常用。我们将在计算几何部分举一大堆类似的例子。
    如果你第一次见到这么诡异的算法，你可能会对这个感兴趣。分治是递归的一种应用。这是我们第一次接触递归运算。下面说的快速排序也是用的递归的思想。递归程序的复杂度分析通常和上面一样，主定理(Master Theory)可以简化这个分析过程。主定理和本文内容离得太远，我们以后也不会用它，因此我们不介绍它，大家可以自己去查。有个名词在这里的话找学习资料将变得非常容易，我最怕的就是一个东西不知道叫什么名字，半天找不到资料。

    归并排序有一个有趣的副产品。利用归并排序能够在O(nlogn)的时间里计算出给定序列里逆序对的个数。你可以用任何一种平衡二叉树来完成这个操作，但用归并排序统计逆序对更方便。我们讨论逆序对一般是说的一个排列中的逆序对，因此这里我们假设所有数不相同。假如我们想要数1, 6, 3, 2, 5, 4中有多少个逆序对，我们首先把这个数列分为左右两段。那么一个逆序对只可能有三种情况：两个数都在左边，两个数都在右边，一个在左一个在右。在左右两段分别处理完后，线性合并的过程中我们可以顺便算出所有第三种情况的逆序对有多少个。换句话说，我们能在线性的时间里统计出A队列的某个数比B队列的某个数大有多少种情况。

A队列：1 3 6         A队列：1 3 6         A队列：1 3 6         A队列：1 3 6         A队列：1 3 6
B队列：2 4 5   ==>   B队列：2 4 5   ==>   B队列：2 4 5   ==>   B队列：2 4 5   ==>   B队列：2 4 5   ……
输出：               输出：1              输出：1 2            输出：1 2 3          输出：1 2 3 4

    每一次从B队列取出一个数时，我们就知道了在A队列中有多少个数比B队列的这个数大，它等于A队列现在还剩的数的个数。比如，当我们从B队列中取出2时，我们同时知道了A队列的3和6两个数比2大。在合并操作中我们不断更新A队列中还剩几个数，在每次从B队列中取出一个数时把当前A队列剩的数目加进最终答案里。这样我们算出了所有“大的数在前一半，小的数在后一半”的情况，其余情况下的逆序对在这之前已经被递归地算过了。

============================华丽的分割线============================

    堆排序(Heap Sort)利用了堆(Heap)这种数据结构（什么是堆？）。堆的插入操作是平均常数的，而删除一个根节点需要花费O(log n)的时间。因此，完成堆排序需要线性时间建立堆（把所有元素依次插入一个堆），然后用总共O(nlogn)的时间不断取出最小的那个数。只要堆会搞，堆排序就会搞。堆在那篇日志里有详细的说明，因此这里不重复说了。

============================华丽的分割线============================

    快速排序(Quick Sort)也应用了递归的思想。我们想要把给定序列分成两段，并对这两段分别进行排序。一种不错的想法是，选取一个数作为“关键字”，并把其它数分割为两部分，把所有小于关键字的数都放在关键字的左边，大于关键字的都放在右边，然后递归地对左边和右边进行排序。把该区间内的所有数依次与关键字比较，我们就可以在线性的时间里完成分割的操作。完成分割操作有很多有技巧性的实现方法，比如最常用的一种是定义两个指针，一个从前往后找找到比关键字大的，一个从后往前找到比关键字小的，然后两个指针对应的元素交换位置并继续移动指针重复刚才的过程。这只是大致的方法，具体的实现还有很多细节问题。快速排序是我们最常用的代码之一，网上的快速排序代码五花八门，各种语言，各种风格的都有。大家可以随便找一个来看看，我说过了我们讲算法但不讲如何实现。NOIp很简单，很多人NOIp前就背了一个快速排序代码就上战场了。当时我把快速排序背完了，抓紧时间还顺便背了一下历史，免得晚上听写又不及格。
    不像归并排序，快速排序的时间复杂度很难计算。我们可以看到，归并排序的复杂度最坏情况下也是O(nlogn)的，而快速排序的最坏情况是O(n^2)的。如果每一次选的关键字都是当前区间里最大（或最小）的数，那么这样将使得每一次的规模只减小一个数，这和插入排序、选择排序等平方级排序没有区别。这种情况不是不可能发生。如果你每次选择关键字都是选择的该区间的第一个数，而给你的数据恰好又是已经有序的，那你的快速排序就完蛋了。显然，最好情况是每一次选的数正好就是中位数，这将把该区间平分为两段，复杂度和前面讨论的归并排序一模一样。根据这一点，快速排序有一些常用的优化。比如，我们经常从数列中随机取一个数当作是关键字（而不是每次总是取固定位置上的数），从而尽可能避免某些特殊的数据所导致的低效。更好的做法是随机取三个数并选择这三个数的中位数作为关键字。而对三个数的随机取值反而将花费更多的时间，因此我们的这三个数可以分别取数列的头一个数、末一个数和正中间那个数。另外，当递归到了一定深度发现当前区间里的数只有几个或十几个时，继续递归下去反而费时，不如返回插入排序后的结果。这种方法同时避免了当数字太少时递归操作出错的可能。

    下面我们证明，快速排序算法的平均复杂度为O(nlogn)。不同的书上有不同的解释方法，这里我选用算法导论上的讲法。它更有技巧性一些，更有趣一些，需要转几个弯才能想明白。
    看一看快速排序的代码。正如我们提到过的那种分割方法，程序在经过若干次与关键字的比较后才进行一次交换，因此比较的次数比交换次数更多。我们通过证明一次快速排序中元素之间的比较次数平均为O(nlogn)来说明快速排序算法的平均复杂度。证明的关键在于，我们需要算出某两个元素在整个算法过程中进行过比较的概率。
    我们举一个例子。假如给出了1到10这10个数，第一次选择关键字7将它们分成了{1,2,3,4,5,6}和{8,9,10}两部分，递归左边时我们选择了3作为关键字，使得左部分又被分割为{1,2}和{4,5,6}。我们看到，数字7与其它所有数都比较过一次，这样才能实现分割操作。同样地，1到6这6个数都需要与3进行一次比较（除了它本身之外）。然而，3和9决不可能相互比较过，2和6也不可能进行过比较，因为第一次出现在3和9，2和6之间的关键字把它们分割开了。也就是说，两个数A(i)和A(j)比较过，当且仅当第一个满足A(i)<=x<=A(j)的关键字x恰好就是A(i)或A(j) （假设A(i)比A(j)小）。我们称排序后第i小的数为Z(i)，假设i<j，那么第一次出现在Z(i)和Z(j)之间的关键字恰好就是Z(i)或Z(j)的概率为2/(j-i+1)，这是因为当Z(i)和Z(j)之间还不曾有过关键字时，Z(i)和Z(j)处于同一个待分割的区间，不管这个区间有多大，不管递归到哪里了，关键字的选择总是随机的。我们得到，Z(i)和Z(j)在一次快速排序中曾经比较过的概率为2/(j-i+1)。
    现在有四个数，2,3,5,7。排序时，相邻的两个数肯定都被比较过，2和5、3和7都有2/3的概率被比较过，2和7之间被比较过有2/4的可能。也就是说，如果对这四个数做12次快速排序，那么2和3、3和5、5和7之间一共比较了12*3=36次，2和5、3和7之间总共比较了8*2=16次，2和7之间平均比较了6次。那么，12次排序中总的比较次数期望值为36+16+6=58。我们可以计算出单次的快速排序平均比较了多少次：58/12=29/6。其实，它就等于6项概率之和，1+1+1+2/3+2/3+2/4=29/6。这其实是与期望值相关的一个公式。
    同样地，如果有n个数，那么快速排序平均需要的比较次数可以写成下面的式子。令k=j-i，我们能够最终得到比较次数的期望值为O(nlogn)。
  
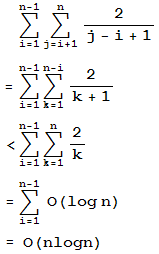
    这里用到了一个知识：1+1/2+1/3+…+1/n与log n增长速度相同，即Σ(1/n)=Θ(log n)。它的证明放在本文的最后。

    在三种O(nlogn)的排序算法中，快速排序的理论复杂度最不理想，除了它以外今天说的另外两种算法都是以最坏情况O(nlogn)的复杂度进行排序。但实践上看快速排序效率最高（不然为啥叫快速排序呢），原因在于快速排序的代码比其它同复杂度的算法更简洁，常数时间更小。

    快速排序也有一个有趣的副产品：快速选择给出的一些数中第k小的数。一种简单的方法是使用上述任一种O(nlogn)的算法对这些数进行排序并返回排序后数组的第k个元素。快速选择(Quick Select)算法可以在平均O(n)的时间完成这一操作。它的最坏情况同快速排序一样，也是O(n^2)。在每一次分割后，我们都可以知道比关键字小的数有多少个，从而确定了关键字在所有数中是第几小的。我们假设关键字是第m小。如果k=m，那么我们就找到了答案——第k小元素即该关键字。否则，我们递归地计算左边或者右边：当k<m时，我们递归地寻找左边的元素中第k小的；当k>m时，我们递归地寻找右边的元素中第k-m小的数。由于我们不考虑所有的数的顺序，只需要递归其中的一边，因此复杂度大大降低。复杂度平均线性，我们不再具体证了。
    还有一种算法可以在最坏O(n)的时间里找出第k小元素。那是我见过的所有算法中最没有实用价值的算法。那个O(n)只有理论价值。

============================华丽的分割线============================

    我们前面证明过，仅仅依靠交换相邻元素的操作，复杂度只能达到O(n^2)。于是，人们尝试交换距离更远的元素。当人们发现O(nlogn)的排序算法似乎已经是极限的时候，又是什么制约了复杂度的下界呢？我们将要讨论的是更底层的东西。我们仍然假设所有的数都不相等。
    我们总是不断在数与数之间进行比较。你可以试试，只用4次比较绝对不可能给4个数排出顺序。每多进行一次比较我们就又多知道了一个大小关系，从4次比较中一共可以获知4个大小关系。4个大小关系共有2^4=16种组合方式，而4个数的顺序一共有4!=24种。也就是说，4次比较可能出现的结果数目不足以区分24种可能的顺序。更一般地，给你n个数叫你排序，可能的答案共有n!个，k次比较只能区分2^k种可能，于是只有2^k>=n!时才有可能排出顺序。等号两边取对数，于是，给n个数排序至少需要log2(n!)次。注意，我们并没有说明一定能通过log2(n!)次比较排出顺序。虽然2^5=32超过了4!，但这不足以说明5次比较一定足够。如何用5次比较确定4个数的大小关系还需要进一步研究。第一次例外发生在n=12的时候，虽然2^29>12!，但现已证明给12个数排序最少需要30次比较。我们可以证明log(n!)的增长速度与nlogn相同，即log(n!)=Θ(nlogn)。这是排序所需要的最少的比较次数，它给出了排序复杂度的一个下界。log(n!)=Θ(nlogn)的证明也附在本文最后。
    这篇日志的第三题中证明log2(N)是最优时用到了几乎相同的方法。那种“用天平称出重量不同的那个球至少要称几次”一类题目也可以用这种方法来解决。事实上，这里有一整套的理论，它叫做信息论。信息论是由香农(Shannon)提出的。他用对数来表示信息量，用熵来表示可能的情况的随机性，通过运算可以知道你目前得到的信息能够怎样影响最终结果的确定。如果我们的信息量是以2为底的，那信息论就变成信息学了。从根本上说，计算机的一切信息就是以2为底的信息量(bits=binary digits)，因此我们常说香农是数字通信之父。信息论和热力学关系密切，比如熵的概念是直接从热力学的熵定义引申过来的。和这个有关的东西已经严重偏题了，这里不说了，有兴趣可以去看《信息论与编码理论》。我对这个也很有兴趣，半懂不懂的，很想了解更多的东西，有兴趣的同志不妨加入讨论。物理学真的很神奇，利用物理学可以解决很多纯数学问题，我有时间的话可以举一些例子。我他妈的为啥要选文科呢。
    后面将介绍的三种排序是线性时间复杂度，因为，它们排序时根本不是通过互相比较来确定大小关系的。

附1：Σ(1/n)=Θ(log n)的证明
    首先我们证明，Σ(1/n)=O(log n)。在式子1+1/2+1/3+1/4+1/5+…中，我们把1/3变成1/2，使得两个1/2加起来凑成一个1；再把1/5,1/6和1/7全部变成1/4，这样四个1/4加起来又是一个1。我们把所有1/2^k的后面2^k-1项全部扩大为1/2^k，使得这2^k个分式加起来是一个1。现在，1+1/2+…+1/n里面产生了几个1呢？我们只需要看小于n的数有多少个2的幂即可。显然，经过数的扩大后原式各项总和为log n。O(logn)是Σ(1/n)的复杂度上界。
    然后我们证明，Σ(1/n)=Ω(log n)。在式子1+1/2+1/3+1/4+1/5+…中，我们把1/3变成1/4，使得两个1/4加起来凑成一个1/2；再把1/5,1/6和1/7全部变成1/8，这样四个1/8加起来又是一个1/2。我们把所有1/2^k的前面2^k-1项全部缩小为1/2^k，使得这2^k个分式加起来是一个1/2。现在，1+1/2+…+1/n里面产生了几个1/2呢？我们只需要看小于n的数有多少个2的幂即可。显然，经过数的缩小后原式各项总和为1/2*logn。Ω(logn)是Σ(1/n)的复杂度下界。

附2：log(n!)=Θ(nlogn)的证明
    首先我们证明，log(n!)=O(nlogn)。显然n!<n^n，两边取对数我们得到log(n!)<log(n^n)，而log(n^n)就等于nlogn。因此，O(nlogn)是log(n!)的复杂度上界。
    然后我们证明，log(n!)=Ω(nlogn)。n!=n(n-1)(n-2)(n-3)….1，把前面一半的因子全部缩小到n/2，后面一半因子全部舍去，显然有n!>(n/2)^(n/2)。两边取对数，log(n!)>(n/2)log(n/2)，后者即Ω(nlogn)。因此，Ω(nlogn)是log(n!)的复杂度下界。

今天写到这里了，大家帮忙校对哦
Matrix67原创
转贴请注明出处]]

    说到概率，有些好玩的东西不得不提。比如，你知道吗，23个人中至少两个人生日相同的概率竟然超过了1/2；假如你们班上有50个人的话，那更不得了，至少两人生日相同的概率达到97% ！如果你会计算这个概率问题的话，你可以亲自证实这一点。本文适宜的读者是知道上述问题怎么算的高中朋友，上述问题也是高中阶段学的一些基本概率知识。
    上面的问题都是简单概率，它包含了一个最基本的原则，即使没有系统地学习过，平常人们也都在无形之中使用它：概率等于你要算的东西除以总的数目。比如。我们要计算23个人中任何两个人都不在同一天生的概率。假设2月29日与其它日期出现概率相同的话（这是为了便于计算我们做出的假设，它有悖于常理），那么它的概率为A(366,23)/366^23。它约为0.493677。因此，至少两人在同一天生的概率为1-0.493677=0.506323。当然，对于“你要算的东西除以总的数目”的认识是片面的，比如“投两个骰子出现的数字和从2到12共有11种可能，问数字和大于10的概率”这一问题的答案并不是2/11，因为这11个点数和出现的概率不是相等的，我们只能从投出的两个数字共6*6=36种情况中进行统计，可能的情况只有(5,6)、(6,5)和(6,6) （不会有人说还有(6,7)之类的吧），答案应该是3/36=1/12。这些都是废话，我不细说了。
    但是，你有想过这个问题吗：要是这些数目是无穷的怎么办？换句话说，统计的东西不是“离散”的怎么办？比如看这样一个问题。明天早上我要和MM约会，但是具体见面时间我忘了，好像是8:00-9:00的某个时候。那么我随便在这个时段中选一个时间去等MM，最多等她半个小时，正好能见到MM的概率是多少（假设MM先到的话不会等我）。这个问题和我们平时见到的问题不同的地方在于，它的“情况”是连续的，不是离散的，不能逐一统计数目。咋办呢？我们注意到，我的时间随机取一个，MM的时间随机取一个，对于某些组合我们是有缘分的（这些组合无穷多）。这些组合正好对应了平面区域上的点。就是说，搞一个横坐标表示我的时间，纵坐标表示MM的时间，那么肯定能画出那么一块区域，区域里的所有点(x,y)对应所有我和MM可能相见的组合。任何一个时间组合有多大的可能落在这个区域呢？由于在矩形区域内点(x,y)是均匀分布的，我们只需要计算一个面积之比就行了。下图中显而易见，答案是3/8。
  

    一个类似的问题是Buffon投针实验。有一个人，叫Buffon。他在地板上画了很多间隔相同的平行线，然后叫了一帮狐朋狗友来，把一些长度相同的针扔在地上。然后，他统计有多少针和地板上的线相交，并宣称可以得到圆周率π的值。换句话说，一根针投到间隔相同的平行线中，与平行线相交的概率和π有关。我们时常感到数学的神奇之处，比如当这个π在很多不该出现的场合莫明其妙的出现时。例如，Stirling近似公式（黑书上的这个公式写错了）出现了π值：n!≈sqrt(2πn) * (n/e)^n （sqrt是开方的意思）。再比如，两个整数互质的概率是6/(π^2)，而无穷级数1+1/4+1/9+1/16+…=(π^2)/6。当然，还有最神奇的e^(πi)+1=0。现在，π又出现在了这样一个看似与圆周率更加没有关系的概率问题中：针与线相交的概率为两倍针的长度除以平行线的间隔再除以π。这个结论的证明和刚才我等MM的问题是一样的。建立这样一个坐标系，x轴是针的中点到离它最近的那根平行线的距离，y轴是针与平行线的夹角。我们一定能做出这样一块“可行区域”，这块可行区域中的点(x,y)所对应的针的位置和平行线相交。然而，这块区域的面积并不像刚才那么简单，它是由一些方程围出来的图形，求这块区域的面积需要使用定积分。这里就不再接着说了，反正能求出来。
    当然，涉及无穷的概率问题还有很多其它的统计方法，这里不说明了。

    有这么一个笑话。据说一个飞机上有炸弹的概率为十万分之一，但某人并不认为这个概率很小。概率小毕竟意味者可能，每天航班这么多，十万分之一确实不是一个小数目。因此，这个人从来不敢坐飞机。有一次，他居然和朋友上了飞机，朋友吃惊地问，你咋不害怕了。他说，飞机上有一个炸弹的概率不是十万分之一么？那么飞机上同时有两个炸弹的概率就是一百亿分之一了，对吧。朋友说，对，一百亿分之一已经很小了。这人说，那好，我自己已经带了一颗炸弹上来。
    从没听过这个笑话的人或许会笑笑说那人真傻，但仔细想想似乎自己解释一下也很困难。这涉及到了条件概率，这在高中课本里（至少在我的高中课本里）没有说过，你把书翻烂了都找不到。
    条件概率，顾名思义，就是有条件的概率。比如，有两个炸弹的概率和知道已经有一个炸弹后存在两个炸弹的概率是不同的。假如我们把有两个炸弹的概率记作P(两个炸弹)=百亿分之一，那么后一个问题就是P(两个炸弹|已经有一个炸弹了)。记号P(A|B)就表示在B已经发生了的情况下，A的概率是多少。后面我们可以知道，它仍然等于十万分之一。
    换一个问题。还记得最前面我们说的“投两个骰子出现的数字和大于10的概率”这个问题吗？它的答案是3/36。现在改一下，如果我们事先就知道至少有一个骰子是6点。那么概率变成多少了（或者问概率变了没有）？很显然，多了一个条件，概率肯定变大了，笨蛋都知道如果有一个骰子搞出那么大一个点数，那赢的几率肯定增加了。关键在于，前面分析过数字和大于10的情况只有(5,6)、(6,5)和(6,6)，它们本来就含有6啊，为什么概率变了。仔细思考发现，原来是总的情况变少了。原来总的情况是36种，但如果知道其中一个骰子是6点的话，情况数就只有11种了。概率变成了3/11，大了不少。我们还需要补充，如果把我们“至少有一个骰子是6点”换成“至少有一个骰子是5点”的话，总的情况数还是11，但3/11将变成2/11，因为有一种情况(6,6)不满足我的已知条件。我们可以纯粹用概率来描述这一个思考过程。如果P(E)表示点数和大于10的概率，P(F)表示至少有一个5点的概率，那么我们要求的是P(E|F)，即已知F发生了，求E发生的概率。于是P(E|F)=P(E∩F)/P(F)。这就是条件概率的公式。简单说明一下就是，E∩F表示满足E的情况和满足F的情况的交集，即同时满足E和F的所有情况。P(E∩F)就是E和F同时发生的概率。这个公式使用原来的非条件概率（总情况数目还是36时的概率）之比来表示条件概率（相当于分式同时除以一个数，就如P(E|F)=2/11=(2/36)/(11/36)）。回到炸弹问题上，P(A|B)就应该等于出现两个炸弹的概率除以出现一个炸弹，他仍然等于一个炸弹的概率。
    高中课本里对“独立事件”的定义是模糊的。其实，现在我们可以很好地给独立事件下定义。如果事件E和事件F独立，那么F就不能影响E，于是P(E|F)=P(E)。把P(E|F)展开，就成了P(E∩F)/P(F)=P(E)，也即P(E∩F)=P(E)*P(F)。这不就是“两个独立事件同时发生的概率”的计算公式么。

 
   条件概率的应用很广泛，下面举个例子。
    有两个人，他们每三句话只有一句是真的（说真话的概率是1/3）。其中一个人说，Matrix67是女的。另一个人说，对。那么，Matrix67的确属于女性的概率是多少？
    这是一个条件概率问题。如果P(E)表示Matrix67是女性的概率，P(F)表示第二个人说“对”的概率，那么我们要求的就是P(E|F)，即在第二个人回答后的情况下第一个人说的话属实的概率。按照公式，它等于P(E∩F)/P(F)。P(E∩F)是说，Matrix67是女的，第二个人也说对，表示的实际意义是两个人都说的真话，他的概率是1/3 * 1/3=1/9。P(F)表示第二个人说“对”的概率，这有两种情况，有可能他说对是因为真的是对的（也即他们俩都说真话），概率仍是1/9；还有一种可能是前一个人撒谎，第二个人也跟着撒谎。他们都说谎的可能性是2/3 * 2/3 =4/9。没有别的情况会使第二个人说“对”了，因此P(F)=1/9+4/9=5/9。按照条件概率的公式，P(E|F)=P(E∩F)/P(F)=(1/9) / (5/9)=1/5。后面我们接着说，这其实是Bayes定理的一个非常隐蔽的形式。

    你或许看过我的这篇日志：http://www.matrix67.com/blog/article.asp?id=87。我用相当长的篇幅介绍了Monty Hall问题。下面所要讲的东西与这个有关，建议你先去看看那篇日志。不看也没啥，我把题目意思在下面引用一下。

    这个问题最初发表在美国的一个杂志上。美国有一个比较著名的杂志叫Parade，它的官方网站是http://www.parade.com。这个杂志里面有一个名字叫做Ask Marylin的栏目，是那种“有问必答”之类的一个Q&A式栏目。96年的时候，一个叫Craig.F.Whitaker的人给这个栏目写了这么一个问题。这个问题被称为Monty Hall Dilemma问题。他这样写到：

    Suppose you're on a game show, and you're given the choice of three doors. Behind one door is a car, behind the others, goats. You pick a door, say number 1, and the host, who knows what's behind the doors, opens another door, say number 2, which has a goat. He says to you, "Do you want to pick door number 3?" Is it to your advantage to switch your choice of doors?

    这个问题翻译过来，就是说，在一个游戏中有三个门，只有一个门后面有车，另外两个门后面是羊。你想要车，但你不知道哪一个门后面有车。主持人让你随便选了一个门。比如说，你选择了1号门。但你还不知道你是否选到了车。然后主持人打开了另一扇门，比如2号。你清楚地看到2号门后面是一只羊。现在主持人给你一个改变主意的机会。请问你是否会换选成3号门？
    对于这个问题，Marylin的回答是：应该换，而且换了后得到车的概率是不换的2倍。

    对于这个问题，十年来涌现出了无数总也想不通的人，有一些冲在最前线的战士以宗教般的狂热传播他们的思想。为了说服这些人，人们发明创造了十几种说明答案的方法，画表格，韦恩图，决策树，假设法，捆绑法（我的那篇日志里也提到一种最常见的解释方法），但是都没用。这群人就是不相信换了拿到车的概率是2/3。他们始终坚定地认为，换与不换的概率同为1/2。下面，我们用一个更科学的方法来计算换了一个门后有车的概率。我们使用刚才学习的条件概率。

  
    上面的图表形象地表明了打开某个门的概率是几分之几。横坐标是选择的第几个门，纵坐标是门后面车与羊的排列。对于有些情况（非主对角线上的格子），主持人打开哪个门只有一种选择，我们把它标在这个格子上；对于对角线上的格子，打开门有两种选择，这两种选择出现的几率相等，因此我们用一条斜线划开。现在，还是假设我们选了1号门，那么此时我选到车的概率显然是1/3，同时，这个车在2号门后面的概率也是1/3，在3号门后面仍为1/3。当主持人打开了第2扇门后，我们需要计算一下这导致原来的这些1/3都变成了什么。我们要求在已经知道主持人亮出二号门后面的羊后车在这三个门后面的概率分别是多少。由于我“最初选择1号门”是整个问题的一个假设（大前提），因此对概率的计算只在我们图表中的第一列进行。我们用事件A、B、C分别表示车在1、2、3号门后的概率，事件D表示主持人打开了2号门。在第一列中，打开2号门的情况占了一格半，因此P(D)=1.5/3。A∩D和C∩D的部分分别用灰色和紫色画了出来，B∩D显然为空集。于是，P(A|D)=P(A∩D)/P(D)=(0.5/3) / (1.5/3)=1/3，结果1号门后面有车的概率仍然是1/3。显然，P(B|D)变成0了，因为P(B∩D)=0，B和D根本不可能同时发生。我们惊奇地发现，3号门后面有车的概率从1/3增加到了2/3，因为P(C|D)=P(C∩D)/P(D)=(1/3) / (1.5/3)=2/3。我们使用条件概率从理论上再一次得到了这个雷打不动的事实。

    我们最后看一个问题。这个问题是条件概率的终极应用，是概率学中一个最重要，应用最广的东西。把下面这个问题搞明白了，从此对概率学的学习就真正入门，可以摆脱“初级”、“菜鸟”的称号了。这就是传说中的Bayes定理。我已经写了五千字了，不想再写了，这保证是我想说的最后一个东西。
    首先你得知道，P(A|B)和P(B|A)是截然不同的两个概念。有些条件概率，正着算P(A|B)容易，把条件反过来算P(B|A)却无从下手，而人们往往更加关心P(B|A)。生活中有很多这样的例子，我们小举一个。
    某个地区性病传播飞快，性病患者高达15%。医院临床实验表明，对有性病的人检测，有95%的人显阳性；对没有性病的人检测，有2%的人阳性。现在，假如某个人搞了一个小MM，突然有点担心，跑到医院去检测，查出了阳性。那么他确实有性病的概率是多少？
    假如事件A是显阳性，B是有性病，我们可以看到在现实生活中P(A|B)比P(B|A)更容易得到。P(A|B)表示对有性病的人进行检测搞出阳性的概率，这可以通过医院里的抽样统计得到，题目中已经说了是95%。但是，P(B|A)就不好说了，它表示对于某个人来说，显阳性意味者真的有性病的概率是多少。这是针对个人的，统计资料通常没有这一项，但人们却往往更关心这个问题。事实上，我们可以通过已有的条件把P(B|A)算出来。把P(B|A)展开，它等于P(B∩A)/P(A)，而因为P(A|B)=P(A∩B)/P(B)，把P(B)乘过去，得到P(B∩A)=P(A∩B)=P(A|B)*P(B)。我们把分子的部分转换成了已知量P(A|B)和P(B)的乘积，它等于95% * 15%。那么P(A)怎么算呢？P(A)是由两种情况构成的，可能是有性病的人显的阳性，即P(A∩B)；也可能是没有性病的人显的阳性，即P(A∩～B)。～B表示B的补集，也可以在B上面画一条横线表示，我这里画不出来，算了。～B就是没有病的人，它的概率是1-15%=85%。P(A∩B)和P(A∩～B)都可以用已有的概率算出来，分别是刚才得到的P(A|B)*P(B)，以及用类似的方法得到的P(A|～B)*P(～B)。。因此整个概率就等于(95% * 15%)/(95% * 15% + 2% * 85%)≈0.8934。这就是Bayes定理的一个具体应用。
    在上面的题里，我们求P(A)时把“显阳性”按照“是否有病”分成了两个不相交的部分，并分别求
出概率后再求和。事实上，对于事件A可以按照B的属性分成多个不相交的部分。此时再完整地叙述一下Bayes定理，大家就不难理解了。如果B1、B2、B3一直到Bn是n个互不相交的事件，而且这n个事件是“一个完整的分类”（即并集是全集，包含了所有可能的情况），那么有公式：

P(B1|A)=[ P(A|B1)*P(B1) ]/[P(A|B1)*P(B1) + P(A|B2)*P(B2) + …+ P(A|Bn)*P(Bn)]

    下面再举一个例子。这个例子和前一个例子非常相似。事实上，它也和前面说我是女的的那个例子如出一辙。它将是我们的最后一个例子，并且我不给解答，写完例子立马走人。解决这个问题有助于理解和联系前面这两个例子。
    我经常约同学单独出去玩。据统计，和一个女同学出去玩的概率高达85%，和一个男同学出去的概率只有15%。现在，某人宣称他看到昨天我和某某男在外面玩。长期观察表明，这人的可信度（说真话的概率）为80%。那么，我昨天真和一个男的出去玩的概率是多少？

Matrix67原创
做人要厚道，转贴请注明出处