不知道大家见过没有，我今天偶然看到，在这里写一下。
    箱子里有两个信封：“一个信封里有1元钱，另一个有10元”有1/2的概率；“一个信封里有10元钱，另一个有100元”有1/4的概率；“一个信封里有100元钱，另一个有1000元”有1/8的概率……也就是说，有1/2^n的概率发生这样的事情，一个信封里有10^(n-1)元钱，另一个信封里有10^n元钱。现在你拿到一个信封，看到了里面有x元钱。给你一次机会换成另外那个信封，问你换不换。
    举个例子，假如我们拿到了100元钱的信封，那么换一个信封得到1000元的概率是得到10元的概率的一半。也就是说，如果我们拿到了x元钱，换一个信封的话有1/3的概率多得9x元，有2/3的概率失去0.9x元。它的期望值是增加2.4x元，这告诉了我们换一个信封显然更好。
    现在的问题是，既然总是换个信封好些，那么为什么我们不一开始就选择另外那个信封呢？

大家可以在下面讨论
我就不参与讨论了，虽然我也不知道是怎么回事

    这个问题让我想到了Newcomb悖论，说有个妖精可以预言你将拿一个箱子还是两个箱子，大家一定见过。

    A highly superior being from another part of the galaxy presents you with two boxes, one open and one closed. In the open box there is a thousand-dollar bill. In the closed box there is either one million dollars or there is nothing. You are to choose between taking both boxes or taking the closed box only. But there's a catch.
    The being claims that he is able to predict what any human being will decide to do. If he predicted you would take only the closed box, then he placed a million dollars in it. But if he predicted you would take both boxes, he left the closed box empty. Furthermore, he has run this experiment with 999 people before, and has been right every time.
    What do you do?
    On the one hand, the evidence is fairly obvious that if you choose to take only the closed box you will get one million dollars, whereas if you take both boxes you get only a measly thousand. You'd be stupid to take both boxes.
    On the other hand, at the time you make your decision, the closed box already is empty or else contains a million dollars. Either way, if you take both boxes you get a thousand dollars more than if you take the closed box only.

    Newcomb悖论是很荒唐的，很不具有数学的科学性。但这篇日志介绍的悖论在科学性上是可以承认的。

    我喜欢各种各样的证明。有史以来我见过的最诡异的证明写在http://www.matrix67.com/blog/article.asp?id=34。人们很难想到这样一些完全找不到突破口的东西竟然能够证明得到。说“没有突破口”还不够确切。准确地说，有些命题多数人认为“怎么可能能够证明”却用了一些技巧使得证明变得非常简单。我看了五色定理的证明，定理宣称若要对地图进行染色使得相邻区域不同色，五种颜色就够了。没看证明之前，我一直在想这个玩意儿可以怎么来证明。直到看了证明过程后才感叹居然如此简单，并且立即意识到四色定理基本上也是这种证明方法。还有，像“一个单位正方形里不可能包含两个互不重叠且边长和超过1的小正方形”这样的命题竟然完全用初中学的那些平面几何知识证明到了，简单得不可思议。关键是，我们能够读懂证明过程，但只有牛人才能想到这个证明过程。
    今天在OIBH上看到了这个帖子，帖子中哲牛分享的一篇文章The Power Of Mathematics恰好说明了这一点。文章中包含有一个推翻“万物皆数”的新思路，相当有启发性。今天我想把我已经知道的四种证明连同新学到的这一个一起写下来。

    如何证明存在一种不能表示为两个整数之比的数？
    古希腊曾有“万物皆数”的思想，这种认为“大自然的一切皆为整数之比”的思想统治了古希腊数学相当长的一段时间，许多几何命题都是根据这一点来证明的。当时的很多数学证明都隐性地承认了“所有数都可以表示为整数之比”，“万物皆数”的思想是古希腊数学发展的奠基。直到有一天，毕达哥拉斯的学生Hippasus告诉他，单位正方形的对角线长度不能表示为两个整数之比。被人们公认的假设被推翻了，大半命题得证的前提被认定是错的，古希腊时代的数学大厦轰然倒塌，数学陷入了历史上的第一次危机。最后，Eudoxus的出现奇迹般地解决了这次危机。今天我们要看的是，为什么单位正方形的对角线长度不能表示为两个整数之比。
      
    单位正方形的对角线长度怎么算呢？从上面的这个图中我们可以看到，如果小正方形的面积是1的话，大正方形的面积就是2。于是单位正方形的对角线是面积为2的正方形的边长。换句话说，Hippasus认为不可能存在某个整数与整数之比，它的平方等于2。
    中学课程中安排了一段反证法。当时有个题目叫我们证根号2是无理数，当时很多人打死了也想不明白这个怎么可能证得到，这种感觉正如前文所说。直到看了答案后才恍然大悟，数学上竟然有这等诡异的证明。
    当然，我们要证明的不是“根号2是无理数”。那个时候还没有根号、无理数之类的说法。我们只能说，我们要证明不存在一个数p/q使得它的平方等于2。证明过程地球人都知道：假设p/q已经不能再约分了，那么p^2=2*q^2，等式右边是偶数，于是p必须是偶数。p是偶数的话，p^2就可以被4整除，约掉等式右边的一个2，可以看出q^2也是偶数，即q是偶数。这样，p也是偶数，q也是偶数，那么p和q就还可以继续约分，与我们的假设矛盾。

    根号2是无理数，我们证明到了。根号3呢？根号5呢？你可能偶尔看到过，Theodorus曾证明它们也是无理数。但Theodorus企图证明17的平方根是无理数时却没有继续证下去了。你可以在网上看到，Theodorus对数学的贡献之一就是“证明了3到17的非平方数的根是无理数”。这给后人留下了一个疑问：怪了，为什么证到17就不证了呢？一个俄国的数学历史家“猜”到了原因。
    他猜测，当时Theodorus就是用类似上面的方法证明的。比如，要证明根号x不是有理数，于是p^2=x*q^2。我们已经证过x=2的情况了，剩下来的质数都是奇数。如果x是奇数且p/q已经不能再约分，那么显然p和q都是奇数。一个奇数2n+1的平方应该等于4(n^2+n)+1，也即8 * n(n+1)/2 + 1，其中n(n+1)/2肯定是一个整数。如果p=2k+1，q=2m+1，把它们代进p^2=x*q^2，有8[k(k+1)/2 – x*m(m+1)/2] = x-1。于是x-1必须是8的倍数。如果当时Theodorus是这么证明的，那么他可以得到这样一个结论，如果x-1不能被8整除，那么它不可能被表示成(p/q)^2。好了，现在3、5、7、11、13减去1后都不是8的倍数，它们的平方根一定不是有理数。在x=9时发生了一次例外，但9是一个平方数。而当x=17时这种证明方法没办法解释了，于是Theodorus就此打住。

    实际上，我们上面说的这么多，在古希腊当时的数学体系中是根本不可能出现的。毕达哥拉斯时代根本没有发展出代数这门学科来，它们掌握的只是纯粹的几何。因此，Hippasus当时的证明不可能像我们现在这样搞点什么奇数x偶数y之类的高科技东西。事实上，Hippasus当时完全运用的平面几何知识来证明他的结论。有人觉得奇怪了，既然当时没有代数，古希腊人是怎么提出“所有数都可以表示为整数之比”的呢？其实古希腊人根本没有提出什么整数之比，这是后人的一个误解。当时毕达哥拉斯学派提出的，叫做“公度单位”。
    两条线段的公度单位，简单的说就是找一个公度量，使得两条线段的长度都是这个公度量的整倍数（于是这个公度量就可以同时作为两条线段的单位长度并用于测量）。寻找公度量的方法相当直观，就是不断把较长的那个线段减去短的那个线段，直到两个线段一样长。熟悉数论的同学一下就明白了这就是欧几里德的辗转相除算法求最大公约数。第一次数学危机的根结就在于，古希腊人理所当然地相信不断地截取线段，总有一个时候会截到两个线段一样长。后来，Hippasus画了这么一张图，告诉大家了一个反例：有可能这个操作会无穷尽地进行下去。
      
    现在看他怎么解释，在图中的BC和BD之间进行辗转相除为什么永远不能停止。把BD减去BC，剩下一段DE。以DE为边做一个新的小正方形DEFG，那么显然DE=EF=FC（∵△EDF为等腰直角且△BEF≌△BCF）。接下来我们应该在BC和DE间辗转相除。BC就等于CD，CD减去一个DE相当于减去一个FC，就只剩下一段DF了。现在轮到DE和DF之间辗转相除，而它们是一个新的正方形的边和对角线，其比例正好与最初的BC和BD相当。于是，这个操作再次回到原问题，并且无限递归下去。最后的结论用我们的话说就是，不存在一个数x使得BC和BD的长度都是x的整倍数。于是，BD/BC不能表示为两个整数之比p/q（否则BD/p=BC/q，这就成为了那个x）。

    有发现上面的代数证明和几何证明之间的共同点吗？它们都是这样的一个思路：假设我已经是满足这个性质的最小的那个了，那么我就可以用一种方法找出更小的一个来，让你无限循环下去，数目越来越小，永

    康托集合是闭区间[0,1]的子集，它的定义如下：给定区间[0,1]，把这个区间分成三段，去掉中间那一端（即去掉(1/3,2/3)），然后把剩下的两段中每一段都按照刚才的方法再进行操作，然后再分，再分，就这样一直挖洞挖下去。在第二次操作后，剩下的区间是[0,1/9]∪[2/9,1/3]∪[2/3,7/9]∪[8/9,1]，再操作一次后区间将由8段构成。最后剩下来的东西是什么呢？你能找到存在于这个集合中的某个具体的元素吗（不包括形如x/(3^n)的端点）？
    我们看到，n次操作后，区间的总长度为(2/3)^n，当n趋于无穷时，区间长度趋于0。但是这并不能说明这个区间里没有任何元素。事实上，我们可以找到至少一个元素。比如，下图中绿色的点表示三等分点，如果P满足AP/AB=A'P/A'B'的话，那么P点始终以比例相同的位置留在某一段上，这样的话即使无限地分下去也不会把它挖掉。
      
    P点的坐标可以通过解这个方程得到：x/1=(x-2/9)/(1/9)。解出来x为1/4。因此，1/4属于康托集合。当然，除了1/4之外还有很多点在这个集合内，我们只是找到了其中一个。事实上，康托集合内的元素有无穷多个。假如我们把所有0到1的数用三进制表示，那么我们发现，去掉的部分都是三进制小数里有数字“1”的。比如，第一次操作时，1/3和2/3的三进制分别是0.1和0.2，我们去掉的是所有从0.1到0.2的数（不包含端点，因为0.1也可以写成0.0222222222…）。第二次操作就去掉了百分位有1的那些数，依此类推。因此，只要一个位于0和1之间的三进制小数能够只用0和2写出，那么它就属于康托集合，因为它永远不会被去掉。刚才的1/4转化为三进制是0.020202…，因此它属于这个集合。显然，这样的数有无穷多个，比如三进制0.002002002…等于十进制的1/13，因此它也属于康托集合。同样，康托集合里不存在孤点，因为在它的左右可以找出无数个属于康托集合的数。应用对角线方法，这个集合里的元素居然还是不可数的。事实上，我们可以建立康托集合与闭区间[0,1]的一一对应关系。
    用以下方法可以把康托集合里的所有数与[0,1]的所有实数对应起来：将康托集合内的任意一个转化为三进制小数后，把每一个数字除以2，再当成是二进制小数转化回来。由于这些三进制小数里只含0和2，因此康托集合里的每个数都恰好能转化为一个[0,1]之间的二进制小数；同样地，二进制小数里的每个“1”变成“2”后也能得到一个康托集合里的数。
      
    设f为定义域在康托集合内的函数，定义f(x)为按照上面的转化方法x所对应的二进制小数，显然这个函数的值域就是[0,1]。比如1/3的三进制为0.0222…，而二进制0.01111…=0.1即十进制的1/2，因此f(1/3)=1/2。我们发现，2/3的三进制为0.2，而0.1的十进制也是1/2。于是f(1/3)=f(2/3)。类似地，那些被挖去的区间的两个端点对应的函数值都相同。现在，我们把这个函数的定义域也扩展到[0,1]：让康托集合里的那些被挖去的区间里的点的函数值与该区间对应的端点相同（在函数图象上看相当于把函数值相等的点用横线段连起来）。于是，f(1/2)=f(1/3)=f(2/3)=1/2，f(1/8)=f(1/9)=f(2/9)=1/4。这个函数一定是上升函数，它在长度为1的区间里从0增长到了1。同时，这个函数也是一个连续函数，因为康托集合与[0,1]的所有实数一一对应。这个函数是一个阶梯状的函数，但是它不是分段的，是连续的。它是无穷多个横线段组成的一个连续函数，除端点无意义以外导数值都是0。或者说，这个函数在不变之中上升。

做人要厚道
转贴请注明出处

    说到概率，有些好玩的东西不得不提。比如，你知道吗，23个人中至少两个人生日相同的概率竟然超过了1/2；假如你们班上有50个人的话，那更不得了，至少两人生日相同的概率达到97% ！如果你会计算这个概率问题的话，你可以亲自证实这一点。本文适宜的读者是知道上述问题怎么算的高中朋友，上述问题也是高中阶段学的一些基本概率知识。
    上面的问题都是简单概率，它包含了一个最基本的原则，即使没有系统地学习过，平常人们也都在无形之中使用它：概率等于你要算的东西除以总的数目。比如。我们要计算23个人中任何两个人都不在同一天生的概率。假设2月29日与其它日期出现概率相同的话（这是为了便于计算我们做出的假设，它有悖于常理），那么它的概率为A(366,23)/366^23。它约为0.493677。因此，至少两人在同一天生的概率为1-0.493677=0.506323。当然，对于“你要算的东西除以总的数目”的认识是片面的，比如“投两个骰子出现的数字和从2到12共有11种可能，问数字和大于10的概率”这一问题的答案并不是2/11，因为这11个点数和出现的概率不是相等的，我们只能从投出的两个数字共6*6=36种情况中进行统计，可能的情况只有(5,6)、(6,5)和(6,6) （不会有人说还有(6,7)之类的吧），答案应该是3/36=1/12。这些都是废话，我不细说了。
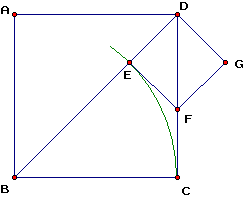
    但是，你有想过这个问题吗：要是这些数目是无穷的怎么办？换句话说，统计的东西不是“离散”的怎么办？比如看这样一个问题。明天早上我要和MM约会，但是具体见面时间我忘了，好像是8:00-9:00的某个时候。那么我随便在这个时段中选一个时间去等MM，最多等她半个小时，正好能见到MM的概率是多少（假设MM先到的话不会等我）。这个问题和我们平时见到的问题不同的地方在于，它的“情况”是连续的，不是离散的，不能逐一统计数目。咋办呢？我们注意到，我的时间随机取一个，MM的时间随机取一个，对于某些组合我们是有缘分的（这些组合无穷多）。这些组合正好对应了平面区域上的点。就是说，搞一个横坐标表示我的时间，纵坐标表示MM的时间，那么肯定能画出那么一块区域，区域里的所有点(x,y)对应所有我和MM可能相见的组合。任何一个时间组合有多大的可能落在这个区域呢？由于在矩形区域内点(x,y)是均匀分布的，我们只需要计算一个面积之比就行了。下图中显而易见，答案是3/8。
  

    一个类似的问题是Buffon投针实验。有一个人，叫Buffon。他在地板上画了很多间隔相同的平行线，然后叫了一帮狐朋狗友来，把一些长度相同的针扔在地上。然后，他统计有多少针和地板上的线相交，并宣称可以得到圆周率π的值。换句话说，一根针投到间隔相同的平行线中，与平行线相交的概率和π有关。我们时常感到数学的神奇之处，比如当这个π在很多不该出现的场合莫明其妙的出现时。例如，Stirling近似公式（黑书上的这个公式写错了）出现了π值：n!≈sqrt(2πn) * (n/e)^n （sqrt是开方的意思）。再比如，两个整数互质的概率是6/(π^2)，而无穷级数1+1/4+1/9+1/16+…=(π^2)/6。当然，还有最神奇的e^(πi)+1=0。现在，π又出现在了这样一个看似与圆周率更加没有关系的概率问题中：针与线相交的概率为两倍针的长度除以平行线的间隔再除以π。这个结论的证明和刚才我等MM的问题是一样的。建立这样一个坐标系，x轴是针的中点到离它最近的那根平行线的距离，y轴是针与平行线的夹角。我们一定能做出这样一块“可行区域”，这块可行区域中的点(x,y)所对应的针的位置和平行线相交。然而，这块区域的面积并不像刚才那么简单，它是由一些方程围出来的图形，求这块区域的面积需要使用定积分。这里就不再接着说了，反正能求出来。
    当然，涉及无穷的概率问题还有很多其它的统计方法，这里不说明了。

    有这么一个笑话。据说一个飞机上有炸弹的概率为十万分之一，但某人并不认为这个概率很小。概率小毕竟意味者可能，每天航班这么多，十万分之一确实不是一个小数目。因此，这个人从来不敢坐飞机。有一次，他居然和朋友上了飞机，朋友吃惊地问，你咋不害怕了。他说，飞机上有一个炸弹的概率不是十万分之一么？那么飞机上同时有两个炸弹的概率就是一百亿分之一了，对吧。朋友说，对，一百亿分之一已经很小了。这人说，那好，我自己已经带了一颗炸弹上来。
    从没听过这个笑话的人或许会笑笑说那人真傻，但仔细想想似乎自己解释一下也很困难。这涉及到了条件概率，这在高中课本里（至少在我的高中课本里）没有说过，你把书翻烂了都找不到。
    条件概率，顾名思义，就是有条件的概率。比如，有两个炸弹的概率和知道已经有一个炸弹后存在两个炸弹的概率是不同的。假如我们把有两个炸弹的概率记作P(两个炸弹)=百亿分之一，那么后一个问题就是P(两个炸弹|已经有一个炸弹了)。记号P(A|B)就表示在B已经发生了的情况下，A的概率是多少。后面我们可以知道，它仍然等于十万分之一。
    换一个问题。还记得最前面我们说的“投两个骰子出现的数字和大于10的概率”这个问题吗？它的答案是3/36。现在改一下，如果我们事先就知道至少有一个骰子是6点。那么概率变成多少了（或者问概率变了没有）？很显然，多了一个条件，概率肯定变大了，笨蛋都知道如果有一个骰子搞出那么大一个点数，那赢的几率肯定增加了。关键在于，前面分析过数字和大于10的情况只有(5,6)、(6,5)和(6,6)，它们本来就含有6啊，为什么概率变了。仔细思考发现，原来是总的情况变少了。原来总的情况是36种，但如果知道其中一个骰子是6点的话，情况数就只有11种了。概率变成了3/11，大了不少。我们还需要补充，如果把我们“至少有一个骰子是6点”换成“至少有一个骰子是5点”的话，总的情况数还是11，但3/11将变成2/11，因为有一种情况(6,6)不满足我的已知条件。我们可以纯粹用概率来描述这一个思考过程。如果P(E)表示点数和大于10的概率，P(F)表示至少有一个5点的概率，那么我们要求的是P(E|F)，即已知F发生了，求E发生的概率。于是P(E|F)=P(E∩F)/P(F)。这就是条件概率的公式。简单说明一下就是，E∩F表示满足E的情况和满足F的情况的交集，即同时满足E和F的所有情况。P(E∩F)就是E和F同时发生的概率。这个公式使用原来的非条件概率（总情况数目还是36时的概率）之比来表示条件概率（相当于分式同时除以一个数，就如P(E|F)=2/11=(2/36)/(11/36)）。回到炸弹问题上，P(A|B)就应该等于出现两个炸弹的概率除以出现一个炸弹，他仍然等于一个炸弹的概率。
    高中课本里对“独立事件”的定义是模糊的。其实，现在我们可以很好地给独立事件下定义。如果事件E和事件F独立，那么F就不能影响E，于是P(E|F)=P(E)。把P(E|F)展开，就成了P(E∩F)/P(F)=P(E)，也即P(E∩F)=P(E)*P(F)。这不就是“两个独立事件同时发生的概率”的计算公式么。

 
   条件概率的应用很广泛，下面举个例子。
    有两个人，他们每三句话只有一句是真的（说真话的概率是1/3）。其中一个人说，Matrix67是女的。另一个人说，对。那么，Matrix67的确属于女性的概率是多少？
    这是一个条件概率问题。如果P(E)表示Matrix67是女性的概率，P(F)表示第二个人说“对”的概率，那么我们要求的就是P(E|F)，即在第二个人回答后的情况下第一个人说的话属实的概率。按照公式，它等于P(E∩F)/P(F)。P(E∩F)是说，Matrix67是女的，第二个人也说对，表示的实际意义是两个人都说的真话，他的概率是1/3 * 1/3=1/9。P(F)表示第二个人说“对”的概率，这有两种情况，有可能他说对是因为真的是对的（也即他们俩都说真话），概率仍是1/9；还有一种可能是前一个人撒谎，第二个人也跟着撒谎。他们都说谎的可能性是2/3 * 2/3 =4/9。没有别的情况会使第二个人说“对”了，因此P(F)=1/9+4/9=5/9。按照条件概率的公式，P(E|F)=P(E∩F)/P(F)=(1/9) / (5/9)=1/5。后面我们接着说，这其实是Bayes定理的一个非常隐蔽的形式。

    你或许看过我的这篇日志：http://www.matrix67.com/blog/article.asp?id=87。我用相当长的篇幅介绍了Monty Hall问题。下面所要讲的东西与这个有关，建议你先去看看那篇日志。不看也没啥，我把题目意思在下面引用一下。

    这个问题最初发表在美国的一个杂志上。美国有一个比较著名的杂志叫Parade，它的官方网站是http://www.parade.com。这个杂志里面有一个名字叫做Ask Marylin的栏目，是那种“有问必答”之类的一个Q&A式栏目。96年的时候，一个叫Craig.F.Whitaker的人给这个栏目写了这么一个问题。这个问题被称为Monty Hall Dilemma问题。他这样写到：

    Suppose you're on a game show, and you're given the choice of three doors. Behind one door is a car, behind the others, goats. You pick a door, say number 1, and the host, who knows what's behind the doors, opens another door, say number 2, which has a goat. He says to you, "Do you want to pick door number 3?" Is it to your advantage to switch your choice of doors?

    这个问题翻译过来，就是说，在一个游戏中有三个门，只有一个门后面有车，另外两个门后面是羊。你想要车，但你不知道哪一个门后面有车。主持人让你随便选了一个门。比如说，你选择了1号门。但你还不知道你是否选到了车。然后主持人打开了另一扇门，比如2号。你清楚地看到2号门后面是一只羊。现在主持人给你一个改变主意的机会。请问你是否会换选成3号门？
    对于这个问题，Marylin的回答是：应该换，而且换了后得到车的概率是不换的2倍。

    对于这个问题，十年来涌现出了无数总也想不通的人，有一些冲在最前线的战士以宗教般的狂热传播他们的思想。为了说服这些人，人们发明创造了十几种说明答案的方法，画表格，韦恩图，决策树，假设法，捆绑法（我的那篇日志里也提到一种最常见的解释方法），但是都没用。这群人就是不相信换了拿到车的概率是2/3。他们始终坚定地认为，换与不换的概率同为1/2。下面，我们用一个更科学的方法来计算换了一个门后有车的概率。我们使用刚才学习的条件概率。

  
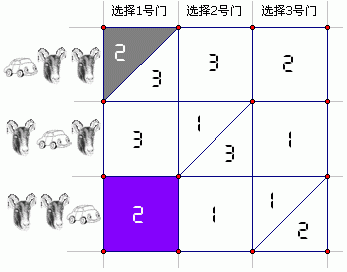
    上面的图表形象地表明了打开某个门的概率是几分之几。横坐标是选择的第几个门，纵坐标是门后面车与羊的排列。对于有些情况（非主对角线上的格子），主持人打开哪个门只有一种选择，我们把它标在这个格子上；对于对角线上的格子，打开门有两种选择，这两种选择出现的几率相等，因此我们用一条斜线划开。现在，还是假设我们选了1号门，那么此时我选到车的概率显然是1/3，同时，这个车在2号门后面的概率也是1/3，在3号门后面仍为1/3。当主持人打开了第2扇门后，我们需要计算一下这导致原来的这些1/3都变成了什么。我们要求在已经知道主持人亮出二号门后面的羊后车在这三个门后面的概率分别是多少。由于我“最初选择1号门”是整个问题的一个假设（大前提），因此对概率的计算只在我们图表中的第一列进行。我们用事件A、B、C分别表示车在1、2、3号门后的概率，事件D表示主持人打开了2号门。在第一列中，打开2号门的情况占了一格半，因此P(D)=1.5/3。A∩D和C∩D的部分分别用灰色和紫色画了出来，B∩D显然为空集。于是，P(A|D)=P(A∩D)/P(D)=(0.5/3) / (1.5/3)=1/3，结果1号门后面有车的概率仍然是1/3。显然，P(B|D)变成0了，因为P(B∩D)=0，B和D根本不可能同时发生。我们惊奇地发现，3号门后面有车的概率从1/3增加到了2/3，因为P(C|D)=P(C∩D)/P(D)=(1/3) / (1.5/3)=2/3。我们使用条件概率从理论上再一次得到了这个雷打不动的事实。

    我们最后看一个问题。这个问题是条件概率的终极应用，是概率学中一个最重要，应用最广的东西。把下面这个问题搞明白了，从此对概率学的学习就真正入门，可以摆脱“初级”、“菜鸟”的称号了。这就是传说中的Bayes定理。我已经写了五千字了，不想再写了，这保证是我想说的最后一个东西。
    首先你得知道，P(A|B)和P(B|A)是截然不同的两个概念。有些条件概率，正着算P(A|B)容易，把条件反过来算P(B|A)却无从下手，而人们往往更加关心P(B|A)。生活中有很多这样的例子，我们小举一个。
    某个地区性病传播飞快，性病患者高达15%。医院临床实验表明，对有性病的人检测，有95%的人显阳性；对没有性病的人检测，有2%的人阳性。现在，假如某个人搞了一个小MM，突然有点担心，跑到医院去检测，查出了阳性。那么他确实有性病的概率是多少？
    假如事件A是显阳性，B是有性病，我们可以看到在现实生活中P(A|B)比P(B|A)更容易得到。P(A|B)表示对有性病的人进行检测搞出阳性的概率，这可以通过医院里的抽样统计得到，题目中已经说了是95%。但是，P(B|A)就不好说了，它表示对于某个人来说，显阳性意味者真的有性病的概率是多少。这是针对个人的，统计资料通常没有这一项，但人们却往往更关心这个问题。事实上，我们可以通过已有的条件把P(B|A)算出来。把P(B|A)展开，它等于P(B∩A)/P(A)，而因为P(A|B)=P(A∩B)/P(B)，把P(B)乘过去，得到P(B∩A)=P(A∩B)=P(A|B)*P(B)。我们把分子的部分转换成了已知量P(A|B)和P(B)的乘积，它等于95% * 15%。那么P(A)怎么算呢？P(A)是由两种情况构成的，可能是有性病的人显的阳性，即P(A∩B)；也可能是没有性病的人显的阳性，即P(A∩～B)。～B表示B的补集，也可以在B上面画一条横线表示，我这里画不出来，算了。～B就是没有病的人，它的概率是1-15%=85%。P(A∩B)和P(A∩～B)都可以用已有的概率算出来，分别是刚才得到的P(A|B)*P(B)，以及用类似的方法得到的P(A|～B)*P(～B)。。因此整个概率就等于(95% * 15%)/(95% * 15% + 2% * 85%)≈0.8934。这就是Bayes定理的一个具体应用。
    在上面的题里，我们求P(A)时把“显阳性”按照“是否有病”分成了两个不相交的部分，并分别求
出概率后再求和。事实上，对于事件A可以按照B的属性分成多个不相交的部分。此时再完整地叙述一下Bayes定理，大家就不难理解了。如果B1、B2、B3一直到Bn是n个互不相交的事件，而且这n个事件是“一个完整的分类”（即并集是全集，包含了所有可能的情况），那么有公式：

P(B1|A)=[ P(A|B1)*P(B1) ]/[P(A|B1)*P(B1) + P(A|B2)*P(B2) + …+ P(A|Bn)*P(Bn)]

    下面再举一个例子。这个例子和前一个例子非常相似。事实上，它也和前面说我是女的的那个例子如出一辙。它将是我们的最后一个例子，并且我不给解答，写完例子立马走人。解决这个问题有助于理解和联系前面这两个例子。
    我经常约同学单独出去玩。据统计，和一个女同学出去玩的概率高达85%，和一个男同学出去的概率只有15%。现在，某人宣称他看到昨天我和某某男在外面玩。长期观察表明，这人的可信度（说真话的概率）为80%。那么，我昨天真和一个男的出去玩的概率是多少？

Matrix67原创
做人要厚道，转贴请注明出处