调和级数是指无穷级数1 + 1/2 + 1/3 + 1/4 + …，即取遍所有正整数n所得到的Σ1/n。虽然n趋于无穷时1/n趋于0，但这个无穷级数却是发散的。一个经典的证明是，把1/3和1/4都缩小到1/4，把1/5、1/6、1/7和1/8都缩小成1/8，把1/9到1/16这8个数全部缩小为1/16，以此类推，这样就可以得到无穷多个1/2，它们的和显然是无穷大的。
    现在，让我们把所有的质数划分为若干个子集，其中质数p属于编号为floor(p/1000)的那个子集（floor()是取下整的意思）。现在，你可以用这样的方式来定义一个“部分的”调和级数：先选出一些质数集合出来，然后列出所有这样的数，它所有的质因子都落在你选的集合里。显然，这样的数有无穷多个，它们的倒数和就形成了一个部分调和级数。例如，选择子集①和子集②，我们可以得到一个无穷级数Σ1/n，其中n取所有这样的数，它可以表示为大于等于1000小于3000的质数的乘积。
    前面我们已经看到，选择所有的集合所构成的无穷级数是发散的。现在的问题是，要想得到一个发散的级数，最少需要选取多少个集合？

Read more…

    无穷个囚犯面向数轴的正方向依次就座，第i个囚犯坐在数轴上坐标为i的地方，他可以看见所有坐标大于i的囚犯头顶上的帽子。看守给每个囚犯戴上黑色或白色的帽子，然后依次叫每个囚犯猜测自己头上的帽子颜色，猜对了的予以释放。另外一点和原来不同的是，囚犯们不能听到其他人的猜测。另外注意到，由于每个人前面都有无穷多个人，因此囚犯们无法通过数他前面的人数来判断出自己的位置，于是我们不得不加上一句：每个人都知道他后面有多少人（即他是第几个被问的）。同样地，事先所有囚犯可以商量出一个策略。你认为这下囚犯们还有什么好办法没？
    这下囚犯已经不能通过自己的猜测来通风报信了，似乎每个人都只能瞎猜，任何人都无法保证自己能猜对。你相信吗，居然有这样的策略，它可以保证除了有限个囚犯之外，其他囚犯全部释放！
    考虑所有可能的颜色序列（你可以简单地想像成01串）。我们说两个颜色序列“无穷远相等”，如果经过了有限多项之后，余下的无穷多项完全相同（即存在某个数x，使得两个串在各自的第x位后面完全重合）。这种关系显然满足自反性、对称性和传递性，是一种等价关系。因此，按照这种有限位后对应相等的关系，我们可以把所有可能的颜色序列划分为一个个等价类。它们的交集为空（两个等价类如果有交集，由传递性它们立即并成了一个更大的等价类），并集为全集（若某序列不属于任何等价类，则它自己就是一个新的等价类），是全集的一个划分。你能想象出一个等价类大致是什么样子的吗？假如把同一个等价类里的所有序列对齐并排放在一起，你从前往后走过去的时候会发现这些序列“越来越相像”。你走得越远，你会发现越来越多的序列开始变得互相重合；当你走到无穷远时，所有的序列都变成一个样了。
    囚犯们事先在每一个等价类中选一个代表元，然后把所有等价类的代表元背下来。到时候，每个人都能够看到他前面无穷多个人的帽子颜色，并且知道他自己在整个序列的位置，于是能立即判断出他们现在所处的颜色序列在哪个等价类里。接下来，他们只需要按照事先背好的代表元来猜就行了。由“无穷远相等”的定义，经过有限次猜测后最终这个代表元会和他们所处的序列重合，于是除了前面有限多个人以外，以后无穷多个人都可以保证猜对。

    你是否觉得这种“策略”很不合理，虽然从逻辑上看每一步推理都是无懈可击的？有人认为，这是选择公理带来的悖论。选择公理是说，给你一系列的集合（可能有无穷多个），那么我们总可以在每一个集合里取出一个元素来。这并不是显然正确的。你不可以依次考虑每个集合，从里面随便取出一个元素来，因为集合个数有可能无穷多个（甚至不可数），这样的操作将永无止境，不允许出现在数学推理过程中。我们需要定义一套系统，使得它对于给定的每一个集合都适用，这样我们就可以“一下子”处理完所有的集合。换句话说，对于一组数量任意多的集合，我们需要定义一个函数f，使得对其中任一集合S，f(S)为S里的一个元素。我们称函数f为选择函数。例如，给出自然数集的所有子集，选择函数f可以定义为“集合中的最小元素”；给出实数集的所有有限长的区间，则选择函数f可以定义为“区间的中点”。但对于某些情况，目前还没有办法用之前已有的公理系统定义出合适的选择函数。比如，目前仍然不清楚，对于实数集的所有非空子集是否存在一个选择函数。但选择函数的存在是很多数学推理的前提假设。因此，我们有必要承认选择公理，构成新的公理体系（即ZFC公理体系）。于是在今后的数学推理中，我们可以假设存在这样一个超级选择函数f，它就是专门用来干这破事的。承认选择公理有可能推出一些与生活经验背道而驰的结论，最著名的就是Banach-Tarski悖论：你可以把一个三维球体分成有限多块，然后拼接组合成两个和原来一样大的球体。上面所提到的100囚犯问题加强版则是选择公理带来的另一个悖论。

参考资料：http://cornellmath.wordpress.com/2007/09/13/the-axiom-of-choice-is-wrong （墙就是强）

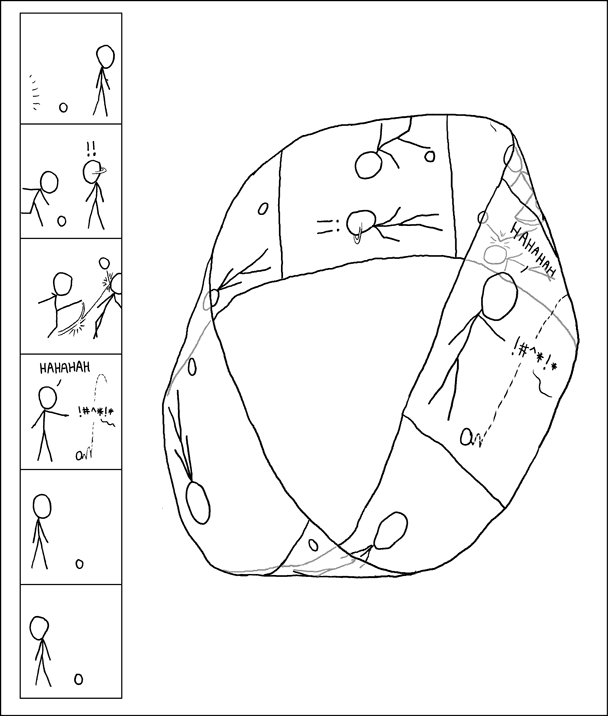
图片来源：http://xkcd.com/381/
知道最妙的是什么吗？是那句HAHAHAH。因为字母H和A恰好都是左右对称的，而且后面多加了一个H使得这句话也变成了回文串。此外，那句!#^*!*也不是随便乱写的。

    Cantor对集合的一些著名的研究让我们更加清楚地认识了无穷这玩意儿。Cantor发现，无穷集合之间也有大小关系，他把这种大小关系叫做集合的势(cardinality)。正整数和正偶数都有无穷多个，但到底谁要多一些呢？我们认为，正整数和正偶数一样多，因为我们可以在它们之间建立起一一对应的关系（乘2除2），因此有多少个正整数就有多少个正偶数，反过来有多少个正偶数我就能找出多少个正整数。于是我们说，正整数集和正偶数集是等势的。
    再来想一个问题，自然数和所有整数哪个多哪个少？答案还是一样多。重新排列一下所有整数，你会看到自然数和整数之间也有一一对应的关系，它们的个数一样多，两个集合也是等势的：

自然数：0,  1,  2,  3,  4,  5,  6,  7,  8, …
   整数：0, -1,  1, -2,  2, -3,  3, -4,  4, …

    Cantor还发现，有理数集与自然数集也是等势的，也就是说有理数和自然数一样多！这个证明方法可谓是数学史上真正的经典：把所有有理数写成最简分数的形式，根据分子和分母的值把它们排列成二维的阵列，然后从1/1出发沿对角线方向蛇形遍历所有的数。第i个遍历到的数与自然数i对应，正有理数集与正整数集也就有了一一对应的关系。注意这里仅仅是正有理数，不过没啥，用刚才证明整数集与自然数集等势的方法，我们也可以把正有理数扩展到全体有理数。
      

    事实上，对于任何一个集合S，如果你能找出一种方法把集合里的所有元素按顺序一个不漏地罗列出来，写成a1, a2, a3, a4, … 的形式，那么这个集合就是和自然数集等势的，因为序列的下标和自然数集就已经构成了一个一一对应的关系。我们把所有与自然数集等势的集合叫做可数集(countable set)，因为它们是可以数出来的。
    并不是所有集合都是可数的。Cantor证明了，实数区间[0,1]是不可数的集合，它的势比自然数集大。你找不出什么方法能把0到1之间的所有实数一个不漏地排列出来。这个证明方法很巧妙，假设你把实数区间[0,1]里的所有数按照某种顺序排列起来，那么我总能找到至少一个0到1之间的实数不在你的列表里。把你的列表上的数全写成0到1之间的小数：

a1 = 0.0147574628…
a2 = 0.3793817237…
a3 = 0.2323232323…
a4 = 0.0004838211…
a5 = 0.9489129145…
………

    那么我就构造这么一个小数，小数点后第一位不等于a1的第一位，小数点后第二位不等于a2的第二位，总之小数点后第i位不等于ai的第i位。这个数属于实数区间[0,1]，但它显然不在你的列表里。这样，我就证明了实数区间是不可数的。

    最近，Matthew H. Baker找到了证明实数区间是不可数集的一种新方法。这种方法同原来的方法完全不同。新的证明方法从一个博弈游戏出发，在两个不同的数学领域间建立起了联系，非常具有启发性。
    A和B两个人在实数区间[0,1]上玩一个游戏。首先，A在(0,1)之间选一个数a1，然后B在(a1,1)里选一个数b1；接着，A在(a1,b1)之间选一个数a2，然后B在(a2,b1)里选一个数b2……总之，以后A和B轮流取数，选的那个数必须位于前面两次选的数之间。可以看到，序列a1, a2, a3, …是一个单增的有界序列，因此游戏无限进行下去，数列{an}最终会收敛到某一个实数c。游戏进行前，A和B约定一个[0,1]的子集S，规定如果最后c∈S，则A胜，否则B胜。
    Baker发现，如果S集为可数集的话，B肯定有必胜策略。如果S集可数，那么B就可以把S集里的数排列成一个序列s1, s2, s3, … 。B的目标就是让序列{an}的极限不等于S集里的任一个数。考虑B的这样一个游戏策略：当B第i次选数时，如果选si合法，那么就选它（这样序列{an}就不能收敛到它了）；否则如果这一步选si不合法，那就随便选一个合法的数（此时序列{an}已经不可能收敛到si了）。这种策略就可以保证A选出的数列的极限不是S集里的任一个数。
    有趣的事情来了。假如A和B约定好的S集就是整个实数区间[0,1]，那么B显然不可能获胜；但如果[0,1]是可数集的话，B是有必胜策略的。于是我们就知道了，[0,1]是不可数集。

消息来源：http://blog.sciencenews.org/mathtrek/2008/01/small_infinity_big_infinity.html
查看更多：https://www.math.gatech.edu/~mbaker/pdf/realgame.pdf

从2007年分形艺术大赛(Benoit Mandelbrot Fractal Art Contest)中选了几个自己感觉不错的图与大家分享。

图片按以下三个原则来选取：
1. 严格符合分形图形的定义
2. 与以往的分形图形风格很不一样
3. 很好看:)

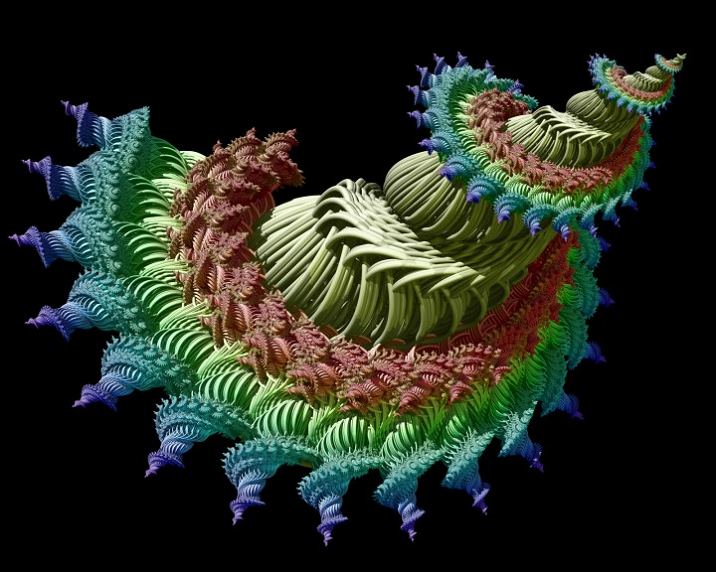
查看全部获奖作品：http://www.fractalartcontests.com/2007/winners.php
查看全部参赛作品：http://www.fractalartcontests.com/2007/entries.php