今天看到一个有趣的证明,来源在这里。

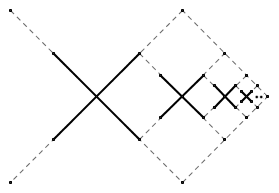
Cantor 集是一个简单而又神奇的分形图形。把 [0, 1] 三等分,挖去中间那一段(即挖去 (1/3, 2/3) ),然后把剩下两段也都分别进行三等分,并挖去各自中间的一段。这样无限地进行下去,最后得到的极限点集就是 Cantor 集了(上面那张图不是分割线,是 Cantor 集的一个示意图)。我们通常把 Cantor 集记作 C 。Cantor 集具有很多神奇的性质:它的 Lebesgue 测度为 0,但它却包含有不可数个点;它里面的每个点都不是孤点,但它却又是无处稠密的。你可以在这里看到一些具体的分析。
Cantor 集还有很多其他的性质。若 A 、 B 是两个集合,定义 A + B = {a + b | a ∈ A 并且 b ∈ B} ,也就是 A 中的某个元素与 B 中的某个元素相加可能得到的所有结果。下面我们将证明,C + C = [0, 2]。