由于勾股数组有无穷多个,因此以原点为圆心的单位圆上有无穷多个有理点。例如,(3,4,5)是一组勾股数,因此(3/5, 4/5)就是单位圆上的一个有理点。将这个圆的半径放大有理数倍,则原来圆周上的有理点现在显然仍是有理点;将这个圆的圆心平移至一个有理点,则同样地,原来圆周上的有理点现在显然仍是有理点。于是我们得到这样一个结论:在平面直角坐标系内,任意一个以有理点为圆心,有理数为半径的圆周上总存在无穷多个有理点。我们不由得想到这样一个有趣的问题:如果一个圆的圆心是无理点(两个坐标中至少有一个不是有理数),那么圆周上的有理点个数还可能是无穷多个吗?若不是的话,最多能有多少个?
无理数
再谈稠密性:令人吃惊的稠密集及其交集
对于数轴上的一个点集,如果说在集合中任意两点之间都能够找到该集合中的另一个点,我们就说该点集处处稠密。例如,全体有理数集合就是稠密的,任意接近的两个有理数之间都存在其它的有理数(比如它们的算术平均值)。这样看来,两个处处稠密的点集似乎是不能共存的,但实际情况并非如此。我们将会看到越来越牛B的例子,它们将让我们对稠密性有一个全新的认识。
1. 在数轴上找出两个处处稠密的点集,它们互不相交。
很简单。全体有理数和全体无理数就是满足条件的两个集合。
2. 在数轴上找出两个处处稠密的不可数点集,它们互不相交。
很狡猾。集合A取全体正有理数和全体负无理数的并集,集合B取全体正无理数和全体负有理数的并集,这两个集合即可满足条件。
3. 在数轴上找出无穷多个处处稠密的点集,它们两两不相交。
令P_i表示第i个素数。则集合S_i := { √P_i + r| r为有理数 }满足条件。为了证明它们两两不相交,假设r_1 + √P_m = r_2 + √P_n,于是(r_1 – r_2)^2 = (√P_n – √P_m)^2,可得√P_m * P_n = ( P_m + P_n – ((r_1 – r_2)^2) )/2。两个素数的乘积的平方根是一个有理数,这显然是荒谬的(很多证明根号2是无理数的方法都可以证实这一点,例如这里的证法http://www.matrix67.com/blog/archives/206)。
根号2是无理数的又一个精彩证明
The American Mathematical Monthly新年第一期中有一段精彩的根号2无理性证明。
假设√2等于p/q,那么对于任意自然数n都有:
(√2)n q = 2n/2 q 当n是偶数时
2(n-1)/2 p 当n是奇数时
无论哪种情况,(√2)n q都是一个自然数。由二项式定理,对任意大的n都有:
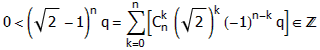
但这显然是不可能的,因为序列(√2 – 1)n q是收敛到0的。
参考资料:http://www.cut-the-knot.org/proofs/sq_root.shtml#proof16
相关文章:五种方法证明根号2是无理数,又一种证明根号2是无理数的方法
经典证明:pi^2是无理数
Proofs from THE BOOK的第六章相当精彩,这一章循序渐进地介绍了多个无理性证明。先证明e是无理数,证明方法和高数课本上的基本相同;试图用类似的办法证明e^2也是无理数时,这一章的内容开始牛B了起来,一些巧妙的变换就让原来的办法继续适用于e^2的证明;加上一些更有趣的技巧,我们还能继续证明e^4也是无理数;当证明对除0外的所有有理数r,e^r都是无理数时,全章达到了高潮。
这一章还提到了pi^2是无理数的证明方法。这个证明建立在Ivan Niven于1947年提出的“pi是无理数”的经典证明的基础上:仅仅是在原证明过程中加了一些微妙的变化就得到了pi^2也是无理数的结论。注意到,“pi^2是无理数”是一个比“pi是无理数”更强的结论。由于有理数的平方还是有理数,因此证到了pi^2是无理数也就说明了pi必然是无理数;但反过来却不行,因为无理数的平方不一定也是无理数,比如根号2的平方就不是无理数。
证明过程用到了一个函数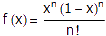 ,其中n是一个任取的大于等于1的常数。可以想像,这个函数的分子部分展开后是一个关于x的整系数多项式,最低次数为n,最高次数为2n。我们将用到这个函数的两个性质:首先,当0<x<1时,显然有0 < f(x) < 1/n!;其次,函数f及其任意阶导数在x=0和x=1处都是整数。为了证明后一个结论,首先注意到当x=0时,不管是多少阶的导数,除了常数项以外其余项都是0;常数项只可能在n<=k<=2n时出现(k表示k阶导数),但此时它等于一个整系数乘以k!/n!,显然也是个整数。另外,由于f(x)=f(1-x),根据复合函数的微分法我们立即得到
,其中n是一个任取的大于等于1的常数。可以想像,这个函数的分子部分展开后是一个关于x的整系数多项式,最低次数为n,最高次数为2n。我们将用到这个函数的两个性质:首先,当0<x<1时,显然有0 < f(x) < 1/n!;其次,函数f及其任意阶导数在x=0和x=1处都是整数。为了证明后一个结论,首先注意到当x=0时,不管是多少阶的导数,除了常数项以外其余项都是0;常数项只可能在n<=k<=2n时出现(k表示k阶导数),但此时它等于一个整系数乘以k!/n!,显然也是个整数。另外,由于f(x)=f(1-x),根据复合函数的微分法我们立即得到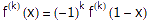 对任意x都成立,当然也就有
对任意x都成立,当然也就有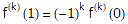 。
。
《什么是数学》读书笔记(二·上):从自然数到实数
今天,我们将从一系列公理开始,从自然数的产生一直说到实数理论的完善。你或许会对数学的“科学性”有一个新的认识。注意,本文的很大一部分内容并非直接来源《什么是数学》,这篇文章可以看作是《什么是数学》中有关章节的一个扩展。
自然数是数学界中最自然的数,它用来描述物体的个数,再抽象一些就是集合的元素个数。在人类文明的最早期,人们就已经很自然地用到了自然数。可以说,自然数是天然产生的,其余的一切都是从自然数出发慢慢扩展演变出来的。数学家Kronecker曾说过,上帝创造了自然数,其余的一切皆是人的劳作。 (God made the natural numbers; all else is the work of man.)
随着一些数学理论的发展,我们迫切地希望对自然数本身有一个数学描述。从逻辑上看,到底什么是自然数呢?历史上对自然数的数学描述有过很多的尝试。数学家Giuseppe Peano提出了一系列用于构造自然数算术体系的公理,称为Peano公理。Peano公理认为,自然数是一堆满足以下五个条件的符号:
1. 0是一个自然数;
2. 每个自然数a都有一个后继自然数,记作S(a);
3. 不存在后继为0的自然数;
4. 不同的自然数有不同的后继。即若a≠b,则S(a)≠S(b);
5. 如果一个自然数集合S包含0,并且集合中每一个数的后继仍在集合S中,则所有自然数都在集合S中。(这保证了数学归纳法的正确性)
形象地说,这五条公理规定了自然数是一个以0开头的单向有序链表。
自然数的加法和乘法可以简单地使用递归的方法来定义,即对任意一个自然数a,有:
a + 0 = a
a + S(b) = S(a+b)
a · 0 = 0
a · S(b) = a + (a·b)
其它运算可以借助加法和乘法来定义。例如,减法就是加法的逆运算,除法就是乘法的逆运算,“a≤b”的意思就是存在一个自然数c使得a+c=b。交换律、结合率和分配率这几个基本性质也可以从上面的定义出发推导出来。
Peano公理提出后,多数人认为这足以定义出自然数的运算,但Poincaré等人却开始质疑Peano算术体系的相容性:是否有可能从这些定义出发,经过一系列严格的数学推导,最后得出0=1之类的荒谬结论?如果一系列公理可以推导出两个互相矛盾的命题,我们就说这个公理体系是不相容的。Hilbert的23个问题中的第二个问题就是问,能否证明Peano算术体系是相容的。这个问题至今仍有争议。