三年前，我曾经给大家介绍过一个单人版的五子棋游戏—— Morpion Solitaire 。这个游戏通常分作 5T 和 5D 两种规则不同的版本。初始时，棋盘上画有 36 个棋子，它们排成一个空心十字架的形状。接下来，你需要在棋盘上添加一个新的棋子，使得它与某四个已有的棋子连成一条线。如此重复，直到在 5T 或者 5D 的规则下再没有满足要求的走法为止。在 5T 规则中，同一方向上的连线不允许有重合； 5D 规则则更加严格，同一方向上的连线在棋子处相接也是不允许的。由于 Morpion Solitaire 游戏不受时间和空间限制，因此它成为了消磨时间的一大利器。不管是在课堂上，餐馆里，还是在飞机上，地铁上，你都可以抓起纸和笔，向自己的最高纪录挑战。
完美的制度是永远不存在。我们可能会产生一种觉得某某制度很完美的错觉，这只是因为我们习惯了它而已。若把这个制度拿出来仔细琢磨琢磨，你会发现它还存在太多的问题。
我们习惯了“多数票当选”的选举制度。每个投票者把自己手中的票投给其中一位候选人，得票数最多的候选人即获胜，因为他的支持者最多。这看上去似乎挺合理。但在实际生活中，这种选举制度并不见得总是合理的——得票数最多的候选人很可能并不是大家喜欢的候选人。有时候，获胜的候选人竟会是最不受欢迎的那个人。
假设有 A 、 B 、 C 、 D 四位候选领导人，其中 A 、 B 、 C 三人的思想、观点、作风都不相上下；候选人 D 则观点偏激、做事极端，他故意与前面三个人作对，一心想在竞选中获胜。虽然 A 、 B 、 C 三人大受好评，但他们却处于一个非常不利的地位：由于得票最多的候选人获胜，三人内部的激烈竞争很可能会使他们都输掉竞选。我们假设只有 34% 的人支持候选人 D ，而另外 66% 的候选人都在 A 、 B 、 C 三人之间犹豫不决。最终， A 、 B 、 C 每个人都只得到 22% 左右的票，候选人 D 以绝对的优势获得胜利。但请注意，候选人 D 却是最不受欢迎的那个人。如果按照投票淘汰制进行选举，候选人 D 将在第一轮就被淘汰，因为最不喜欢他的人达到了 66% 。
有人会说，那么干脆以后选举都搞投票淘汰制，每个投票者每轮都选出一位仍未淘汰的人中自己最讨厌的，问题不就解决了吗？这样也有问题——对称地，如果 A 、 B 、 C 三人都很讨厌，投票者会在他们三人之间纠结， D 却反而处于了最不利的地位。因此，要想彻底避免这种问题，我们还得想点儿别的着。
昨天的消息：一位 HP 的研究员 Vinay Deolalikar 宣称自己证明了 NP 问题，得出了 P≠NP 的结论。 P 是否等于 NP ，这是计算机科学领域中最困难的问题之一，也是意义最深远的问题之一，长期以来一直备受争议。如果这个问题获得解决，将会在各个科学领域中引起轰动。 Vinay Deolalikar 的整个证明有 100 多页，详细的论文可以在这里看到：
http://www.win.tue.nl/~gwoegi/P-versus-NP/Deolalikar.pdf
Stanford 的博士后 randomwalker 看完证明后表示，很多迹象表明，这个证明很有可能是正确的。
－－－－－－－－－－－－－－－－－－－－－－－－－－－
今天早晨的消息： Morley Davidson 、 John Dethridge 、 Herbert Kociemba 和 Tomas Rokicki 宣称，他们已经利用计算机，完美地解决了魔方问题。他们验证了，任何一种魔方的初始状态都可以在 20 步以内解出。他们将 43,252,003,274,489,856,000 种初始状态分为了 2,217,093,120 组，再利用对称性和集合覆盖将规模缩小到了 55,882,296 组。他们的程序可以在 20 秒左右求解出一组问题的解法，最终利用 Google 提供的强大的计算机，彻底解决了魔方问题。
利用组合数学，我们能够证明，存在一种魔方初始状态，它需要至少 18 步才能解决。 1995 年， Michael Reid 找到了一种最少需要 20 步才能获解的魔方初始状态，因而将魔方问题的下界提高到了 20 。此后，数学家们猜想，任意给定一个魔方的初始状态，最多 20 步就能解决。 2008 年， Tomas Rokicki 和 John Welborn 证明了，任意一个魔方初始状态都可以在 22 步以内解决。 2010 年 7 月，这个上界终于降低到了 20 ，从而完成了对魔方最优解问题数十年来的探索。
详细的研究成果见这里：
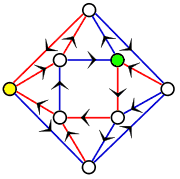以色列数学家Avraham Trakhtman最近解决了一个非常有名的数学难题——公路涂色问题(Road Coloring Problem)。这是图论中的一个著名猜想，最早由Benjamin Weiss和Roy Adler在1970年提出。63岁的Avraham用铅笔草草写下了仅仅8页的证明过程，出人意料地解决了这个问题。该问题的解决对道路规划等很多现实社会中的问题都有帮助。
给定一个有向图G（即图中的每一条边都单向地从某个顶点指向另一个顶点），其中每一个点的出度（向外走的边的条数）都为k。假设我们用k种颜色对图G中的所有边进行染色，使得每个点的k条出边的颜色都不相同，并且对于每一个顶点v，总存在一个颜色序列，使得不管你从哪里出发，按照这个颜色序列不断走下去，最终都能到达顶点v。我们称满足这些条件的涂色方案叫做一个同步着色(synchronizing coloring)。Benjamin Weiss和Roy Adler猜想，如果一个有向图是强连通的（任两点间都可互相到达）并且是非周期性的（所有环的长度的最大公约数为1），则该图一定存在同步着色方案。例如，右面这个图就是一个合法的同步着色方案，每个点的两条出边恰好一红一蓝。我们可以找几个点简单验证一下：不管你在哪里，按“蓝-红-红”走最终总会到那个黄色的点；类似地，不断按“蓝-蓝-红”走，不管出发点在哪里你最后总会走到绿色的点。
这个猜想的完整证明过程可以在这篇论文里找到。论文只有几页，估计我应该能看懂，看懂了的话我会更新出来的。
图灵机是1936年Alan Turing提出的一个计算机模型。这种计算机由一个一维数组（或者叫磁带）构成，还有一个可以左右移动的指针。磁带上每个格子里都有一种颜色（共可从m种颜色中选择），指针本身则可以是n种状态中的一种。给定一个m*n的表格，你就定义了一个图灵机。这个表格告诉机器，如果当前指针的状态是x，它所指的格子的颜色是y，那么下一步机器应该把这个格子染成什么颜色，然后指针应该左移一位还是右移一位，指针的新状态又是什么。有了一个图灵机后，我们便可以把它当做一个计算机进行数据处理了。我们可以给这个图灵机编写一个初始状态（也就相当于现在所说的程序和数据），让它按照这个表格不断执行下去，对数据进行处理并“输出”适当的结果来。
能够模拟其它所有图灵机的图灵机叫做“通用图灵机”(UTM, Universal Turing Machine)。不是所有的图灵机都是通用的：很多图灵机只能完成一些特定的运算，而只有通用图灵机才能完成更一般的操作，是一台“通用的”机器。这些通用图灵机就像现代计算机一样，可以用来编程执行各种各样的操作，能实现现代计算机的各种功能。我们经常说一种程序语言是图灵完全的(Turing Complete)，指的就是这种语言等价于通用图灵机，能够执行任何一种复杂的数学运算。
50年代起，科学家们疯狂地寻找通用图灵机，所需要的颜色数和状态数越来越小。最好的结果是1967年由Marvin Minsky得到的，他发现了一个7,4通用图灵机，即一个只需要7种状态，4种颜色的通用图灵机。人们开始好奇，最简单的通用图灵机是什么样子的。2002年，Stephen Wolfram（没错，就是MathWorld的那个Wolfram）做出了一个重大的突破：他发现了一个2,5通用图灵机，并且给出了一个很可能是通用图灵机的2,3图灵机。很早以前人们就证明了，不存在2,2的通用图灵机；因此如果Wolfram提出的2,3图灵机是通用图灵机的话，它就是最小的通用图灵机了。但Wolfram始终不能证明这个2,3图灵机是通用的，于是在今年三月份用25000美元悬赏征解。
昨天，英国伯明翰大学的一名20岁在校大学生Alex Smith提交了一篇55页的论文，证明了Wolfram的2,3图灵机与另一个已知的通用机器等价，从而证明了2,3图灵机是最简单的通用图灵机，证实了这个很早就已经提出的猜想，解决了长期以来计算机科学界的一大疑问。这是一个意义非常重大的突破，无疑是信息学界中的一件激动人心的大事。