Hash表是一个很有用的数据结构，它用O(N)的空间描述一个元素在0到N-1范围内的集合，支持常数级别的添加、删除和查询。遗憾的是，Hash表不能在常数时间内批量删除元素，返回全部元素也需要O(N)的时间，而理论上说这几个操作可以做的更好。现在，你能否设计一个数据结构，它同样占用O(N)的空间，支持常数时间的添加、删除、查询、清空（删除所有元素）、势查询（返回元素个数），以及O(n)时间的元素遍历（其中n表示集合中的元素个数）。

查看更多 »

    Anagram是一个比较流行的英文文字游戏，本Blog之前曾经介绍过，这里我再提一下。Anagram就是把一个词或者一句话里的字母重新排列，组成一个新的单词或句子，通常前后两者有一种讽刺的意味。比如，Dormitory = Dirty Room，或者Desperation = A Rope Ends It。创作一个有意思的Anagram并不是一件容易的事，你很可能需要计算机的帮助才能找到合适的词。例如，我们可以利用Hash表瞬间找出与给定单词所使用的字母完全相同的单词。我们可以把字典中每个单词的字母按照字母顺序重新排列，于是对单词dame和made操作后的结果都是adem，这样的话使用字母完全相同的单词就对应了一个唯一的Hash值，我们就可以方便地把它们归在一起。
    而实际上，这个Hash表往往没什么用。一个Anagram很可能是由多个单词构成的，因此我们更希望知道，使用某个单词中的字母（不一定全部使用）可以构造出哪些新的单词。例如，我输入单词dormitory，则程序可以输出dirty, motor, trim, dry, room等单词。很多Anagram辅助程序都有这样的功能，并且这也单独作为一个文字游戏存在。我们称这种只用到一部分给定字母的单词叫做不完全Anagram。假如字典里共有n个单词，输入数据长度为l，那么你怎样才能找出所有的不完全Anagram？一种方法是遍历所有n个单词，依次判断每个单词是否合法；另一种方法则是枚举输入数据的2^l子集，对每个子集在之前建立的Hash表中查询一次。现在，你能否想出一个数据结构，使得你的Anagram辅助程序能够以最快的速度输出任何一个给定单词的不完全Anagram？













































  
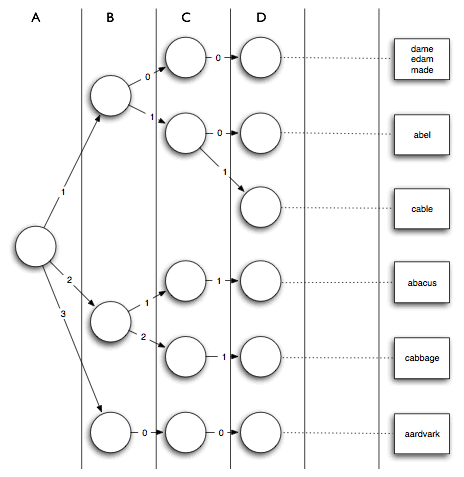
    答案比你想像的更简单，这是一个非常简单的数据结构。我们建立一棵高度为26的树，按照每个字母出现的次数像Trie一样插入到树中。比如，abacus有2个a，于是插入到根的第二个子树里，接下来数出字母b的个数为1，并继续沿标号为1的边往下走，依此类推。最后，所有的数据都存放在对应的叶子节点上。查询时，在每个节点上只需数一数输入数据中对应字母的个数N，沿着标号小于等于N的边往下走就行了。
    下面是一个非常有趣的问题：这个数据结构还有什么优化的余地？比如，单词在树中是按照从A到Z的顺序依次分类，但实际上我们可以任意调整这个顺序。那么，你觉得建这棵树时是先按E、T等常用字母的个数分类好，还是先按照Q、Z等不常用字母的个数分类好？这个问题很简单，留给大家思考吧。
    另一个比较类似的东西是用于拼写检查的数据结构。这两个有趣的数据结构都是我在这里看到的。

做人要厚道
转贴请注明出处

    除了字符串匹配、查找回文串、查找重复子串等经典问题以外，日常生活中我们还会遇到其它一些怪异的字符串问题。比如，有时我们需要知道给定的两个字符串“有多像”，换句话说两个字符串的相似度是多少。1965年，俄国科学家Vladimir Levenshtein给字符串相似度做出了一个明确的定义叫做Levenshtein距离，我们通常叫它“编辑距离”。字符串A到B的编辑距离是指，只用插入、删除和替换三种操作，最少需要多少步可以把A变成B。例如，从FAME到GATE需要两步（两次替换），从GAME到ACM则需要三步（删除G和E再添加C）。Levenshtein给出了编辑距离的一般求法，就是大家都非常熟悉的经典动态规划问题。
    在自然语言处理中，这个概念非常重要，例如我们可以根据这个定义开发出一套半自动的校对系统：查找出一篇文章里所有不在字典里的单词，然后对于每个单词，列出字典里与它的Levenshtein距离小于某个数n的单词，让用户选择正确的那一个。n通常取到2或者3，或者更好地，取该单词长度的1/4等等。这个想法倒不错，但算法的效率成了新的难题：查字典好办，建一个Trie树即可；但怎样才能快速在字典里找出最相近的单词呢？这个问题难就难在，Levenshtein的定义可以是单词任意位置上的操作，似乎不遍历字典是不可能完成的。现在很多软件都有拼写检查的功能，提出更正建议的速度是很快的。它们到底是怎么做的呢？1973年，Burkhard和Keller提出的BK树有效地解决了这个问题。这个数据结构强就强在，它初步解决了一个看似不可能的问题，而其原理非常简单。

    首先，我们观察Levenshtein距离的性质。令d(x,y)表示字符串x到y的Levenshtein距离，那么显然：

1. d(x,y) = 0 当且仅当 x=y  （Levenshtein距离为0 <==> 字符串相等）
2. d(x,y) = d(y,x)     （从x变到y的最少步数就是从y变到x的最少步数）
3. d(x,y) + d(y,z) >= d(x,z)  （从x变到z所需的步数不会超过x先变成y再变成z的步数）

    最后这一个性质叫做三角形不等式。就好像一个三角形一样，两边之和必然大于第三边。给某个集合内的元素定义一个二元的“距离函数”，如果这个距离函数同时满足上面说的三个性质，我们就称它为“度量空间”。我们的三维空间就是一个典型的度量空间，它的距离函数就是点对的直线距离。度量空间还有很多，比如Manhattan距离，图论中的最短路，当然还有这里提到的Levenshtein距离。就好像并查集对所有等价关系都适用一样，BK树可以用于任何一个度量空间。

    建树的过程有些类似于Trie。首先我们随便找一个单词作为根（比如GAME）。以后插入一个单词时首先计算单词与根的Levenshtein距离：如果这个距离值是该节点处头一次出现，建立一个新的儿子节点；否则沿着对应的边递归下去。例如，我们插入单词FAME，它与GAME的距离为1，于是新建一个儿子，连一条标号为1的边；下一次插入GAIN，算得它与GAME的距离为2，于是放在编号为2的边下。再下次我们插入GATE，它与GAME距离为1，于是沿着那条编号为1的边下去，递归地插入到FAME所在子树；GATE与FAME的距离为2，于是把GATE放在FAME节点下，边的编号为2。
      
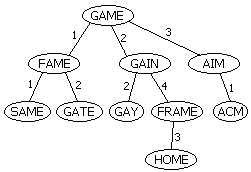
    查询操作异常方便。如果我们需要返回与错误单词距离不超过n的单词，这个错误单词与树根所对应的单词距离为d，那么接下来我们只需要递归地考虑编号在d-n到d+n范围内的边所连接的子树。由于n通常很小，因此每次与某个节点进行比较时都可以排除很多子树。
    举个例子，假如我们输入一个GAIE，程序发现它不在字典中。现在，我们想返回字典中所有与GAIE距离为1的单词。我们首先将GAIE与树根进行比较，得到的距离d=1。由于Levenshtein距离满足三角形不等式，因此现在所有离GAME距离超过2的单词全部可以排除了。比如，以AIM为根的子树到GAME的距离都是3，而GAME和GAIE之间的距离是1，那么AIM及其子树到GAIE的距离至少都是2。于是，现在程序只需要沿着标号范围在1-1到1+1里的边继续走下去。我们继续计算GAIE和FAME的距离，发现它为2，于是继续沿标号在1和3之间的边前进。遍历结束后回到GAME的第二个节点，发现GAIE和GAIN距离为1，输出GAIN并继续沿编号为1或2的边递归下去（那条编号为4的边连接的子树又被排除掉了）……
    实践表明，一次查询所遍历的节点不会超过所有节点的5%到8%，两次查询则一般不会17-25%，效率远远超过暴力枚举。适当进行缓存，减小Levenshtein距离常数n可以使算法效率更高。

Matrix67原创
做人要厚道 转贴请注明出处

看看下面两道题，它的解答非常简单，即使没学过信息学的人也可以想到答案。你能在多短的时间内想出问题的算法来？一小时？一分钟？一秒钟？

1. 给你一个长度为N的链表。N很大，但你不知道N有多大。你的任务是从这N个元素中随机取出k个元素。你只能遍历这个链表一次。你的算法必须保证取出的元素恰好有k个，且它们是完全随机的（出现概率均等）。

2. 给你一个数组A[1..n]，请你在O(n)的时间里构造一个新的数组B[1..n]，使得B[i]=A[1]*A[2]*...*A[n]/A[i]。你不能使用除法运算。

Solution:
1. 遍历链表，给每个元素赋一个0到1之间的随机数作为权重（像Treap一样），最后取出权重最大的k个元素。你可以用一个堆来维护当前最大的k个数。
2. 从前往后扫一遍，然后从后往前再扫一遍。也就是说，线性时间构造两个新数组，P[i]=A[1]*A[2]*...*A[i]，Q[i]=A[n]*A[n-1]*...*A[i]。于是，B[i]=P[i-1]*Q[i+1]。

突然想到，给别人(MM?)介绍信息学时，用这两道题当例子挺合适的。

    寒假时没事写了这几个代码，算是我几个月后重操键盘了。这是几道经典题目，可能有人需要，再加上昨天搞JavaScript改过去改过来把PJBlog改得面目全非终于实现了代码高亮忍不住想Show一下，于是把这些代码（连同题目）发了上来。

标准的网络流题目代码

Problem : goods
货物运输

问题描述
    你第一天接手一个大型商业公司就发生了一件倒霉的事情：公司不小心发送了一批次品。很不幸，你发现这件事的时候，这些次品已经进入了送货网。这个送货网很大，而且关系复杂。你知道这批次品要发给哪个零售商，但是要把这批次品送到他手中有许多种途径。送货网由一些仓库和运输卡车组成，每辆卡车都在各自固定的两个仓库之间单向运输货物。在追查这些次品的时候，有必要保证它不被送到零售商手里，所以必须使某些运输卡车停止运输，但是停止每辆卡车都会有一定的经济损失。你的任务是，在保证次品无法送到零售商的前提下，制定出停止卡车运输的方案，使损失最小。

输入格式
    第一行：两个用空格分开的整数N(0<=N<=200)和M(2<=M<=200)。N为运输卡车的数目，M为仓库的数目。1号仓库是公司发货的出口，仓库M属于零售商。
    第二行到第N+1行：每行有三个整数，Si、Ei和Ci。Si和Ei(1<=Si,Ei<=M)分别表示这辆卡车的出发仓库和目的仓库，Ci(0<=Ci<=10,000,000)是让这辆卡车停止运输的损失。

输出格式
    输出一个整数，即最小的损失数。

样例输入
5 4
1 2 40
1 4 20
2 4 20
2 3 30
3 4 10

样例输出
50

样例说明
         40
      1------>2
      |      /|
      |     / |
    20|    /  |30
      |  20   |
      |  /    |
      | /     |
      \/_     V
      4<------3
          10

    如图，停止1->4、2->4、3->4三条卡车运输线路可以阻止货物从仓库1运输到仓库4，代价为20+20+10=50。

数据规模
    对于50%的数据，N,M<=25
    对于100%的数据，N,M<=200

program goods;

const
   MaxN=200;
   MaxM=200;
   Infinite=Maxlongint;

type
   rec=record
         node,father:integer;
         minf:longint;
       end;

var
   f,c:array[1..MaxN,1..MaxN]of longint;
   queue:array[1..MaxN]of rec;
   hash:array[1..MaxN]of boolean;
   n,m,closed,open:integer;

procedure readp;
var
   i,x,y:integer;
   t:longint;
begin
   readln(m,n);
   for i:=1 to m do
   begin
      readln(x,y,t);
      c[x,y]:=c[x,y]+t;
   end;
end;

function FindPath:boolean;

   procedure Init;
   begin
      fillchar(hash,sizeof(hash),0);
      fillchar(queue,sizeof(queue),0);
      closed:=0;
      open:=1;
      queue[1].node:=1;
      queue[1].father:=0;
      queue[1].minf:=Infinite;
      hash[1]:=true;
   end;

   function min(a,b:longint):longint;
   begin
      if a<b then min:=a
      else min:=b;
   end;

var
   i,NodeNow:integer;
begin
   Init;
   repeat
      inc(closed);
      NodeNow:=queue[closed].node;
      for i:=1 to n do if not hash[i] then
         if (f[NodeNow,i]<c[NodeNow,i]) then
         begin
            inc(open);
            queue[open].node:=i;
            queue[open].father:=closed;
            queue[open].minf:=min(queue[closed].minf,c[NodeNow,i]-f[NodeNow,i]);
            hash[i]:=true;
            if i=n then exit(true);
         end;
   until closed>=open;
   exit(false);
end;

procedure AddPath;
var
   i,j:integer;
   delta:longint;
begin
   delta:=queue[open].minf;
   i:=open;
   repeat
      j:=queue[i].father;
      inc(f[queue[j].node,queue[i].node],delta);
      dec(f[queue[i].node,queue[j].node],delta);
      i:=j;
   until i=0;
end;

procedure writep;
var
   i:integer;
   ans:longint=0;
begin
   for i:=1 to n do
      ans:=ans+f[1,i];
   writeln(ans);
end;

{====main====}
begin
   assign(input,'goods.in');
   reset(input);
   readp;
   close(input);

   while FindPath do AddPath;

   assign(output,'goods.out');
   rewrite(output);
   writep;
   close(output);
end.


统计逆序对 Treap版

Problem : inverse
逆序对

问题描述
    在一个排列中，前面出现的某个数比它后面的某个数大，即当Ai>Aj且i<j时，则我们称Ai和Aj为一个逆序对。给出一个1到N的排列，编程求出逆序对的个数。

输入格式
    第一行输入一个正整数N；
    第二行有N个用空格隔开的正整数，这是一个1到N的排列。

输出格式
    输出输入数据中逆序对的个数。

样例输入
4
3 1 4 2

样例输出
3

样例说明
    在输入数据中，(3,1)、(3,2)和(4,2)是仅有的三个逆序对。

数据规模
    对于30%的数据，N<=1000；
    对于100%的数据，N<=100 000。

program inverse;

const
   MaxH=Maxlongint;
  
type
   p=^rec;
   rec=record
          v,s,h:longint;
          left,right:p;
       end;

var
   header:p=nil;
   ans:int64=0;

procedure CalcuS(var w:p);
begin
   w^.s:=1;
   if w^.right<>nil then inc(w^.s,w^.right^.s);
   if w^.left<>nil then inc(w^.s,w^.left^.s);
end;

function RotateLeft(w:p):p;
var
   tmp:p;
begin
   tmp:=w^.left;
   w^.left:=tmp^.right;
   tmp^.right:=w;
   exit(tmp);
end;

function RotateRight(w:p):p;
var
   tmp:p;
begin
   tmp:=w^.right;
   w^.right:=tmp^.left;
   tmp^.left:=w;
   exit(tmp);
end;

function Insert(a:longint;w:p):p;
begin
  if w=nil then
  begin
     new(w);
     w^.v:=a;
     w^.h:=random(MaxH);
     w^.s:=1;
     w^.left:=nil;
     w^.right:=nil;
  end

  else if a<w^.v then
  begin
     ans:=ans+1;
     if w^.right<>nil then ans:=ans+w^.right^.s;
     w^.left:=Insert(a,w^.left);
     if w^.left^.h<w^.h then
     begin
        w:=RotateLeft(w);
        CalcuS(w^.right);
     end else
        CalcuS(w^.left);
  end

  else if a>w^.v then
  begin
     w^.right:=Insert(a,w^.right);
     if w^.right^.h<w^.h then
     begin
        w:=RotateRight(w);
        CalcuS(w^.left);
     end else
        CalcuS(w^.right);
  end;

  exit(w);
end;

{====main====}
var
   n,i,t:longint;
begin
   randseed:=2910238;
  
   assign(input,'inverse.in');
   reset(input);
   readln(n);
   for i:=1 to n do
   begin
      read(t);
      header:=Insert(t,header);
   end;
   close(input);

   assign(output,'inverse.out');
   rewrite(output);
   writeln(ans);
   close(output);
end.

USACO经典题目：矩形颜色（离散化+扫描）

Problem : rect
矩形颜色

问题描述
　　N个不同颜色的不透明长方形(1<=N<=1000)被放置在一张宽为A长为B的白纸上。这些长方形被放置时，保证了它们的边与白纸的边缘平行。所有的长方形都放置在白纸内，所以我们会看到不同形状的各种颜色。坐标系统的原点(0,0)设在这张白纸的左下角，而坐标轴则平行于边缘。

输入数据
    每行输入的是放置长方形的方法。第一行输入的是那个放在最底下的长方形（即白纸）。
    第一行：A、B和N，由空格分开(1<=A,B<=10,000)
    第二到N+1行：每行为五个整数llx,lly,urx,ury,color。这是一个长方形的左下角坐标，右上角坐标和颜色。颜色1和底部白纸的颜色相同。

输出数据
    输出文件应该包含一个所有能被看到的颜色连同该颜色的总面积的清单（即使颜色的区域不是连续的），按color的增序顺序。
    不要打印出最后不能看到的颜色。

样例输入
20 20 3
2 2 18 18 2
0 8 19 19 3
8 0 10 19 4

样例输出
1 91
2 84
3 187
4 38

数据规模
    对于50%的数据，A,B<=300，N<=60；
    对于100%的数据，A,B<=10000，N<=1000。

program rect;

const
   MaxN=1000;       { Rect number in the Worst Case }
   MaxCol=1000;     { Color number in the Worst Case }
   Infinity=Maxint; { Set to be Heap[0] }

type
   RecSeg=record
            y,x1,x2,order:integer;
          end;
var
   xar,heap:array[0..MaxN*2+2]of integer; { Array of All X-Value and Heap, respectively }
   color:array[1..MaxN+1]of integer;      { Index of Color corresponding to order}
   ans:array[1..MaxCol]of longint;        { Answers to be print }
   seg:array[0..MaxN*2+2]of RecSeg;       { Horizontal Segments }
   hash:array[1..MaxN*2+2]of boolean;     { Determine if a Segment has been scanned }
   n,HeapSize:integer;

procedure SwapInt(var a,b:integer);
var
   tmp:integer;
begin
   tmp:=a;
   a:=b;
   b:=tmp;
end;

procedure SwapRec(var a,b:RecSeg);
var
   tmp:RecSeg;
begin
   tmp:=a;
   a:=b;
   b:=tmp;
end;

procedure DataInsert(start,x1,y1,x2,y2,col,order:integer);
var
   tmp:RecSeg;
begin
   xar[start]:=x1;
   xar[start+1]:=x2;
   color[start div 2+1]:=col;

   tmp.order:=order;
   tmp.y:=y1;
   tmp.x1:=x1;
   tmp.x2:=x2;
   seg[start]:=tmp;

   tmp.y:=y2;
   seg[start+1]:=tmp;
end;

procedure Readp;
var
   a,b,x1,x2,y1,y2,col,i:integer;
begin
   readln(a,b,n);
   n:=n+1;
   DataInsert(1,0,0,a,b,1,1);
   for i:=2 to n do
   begin
      readln(x1,y1,x2,y2,col);
      DataInsert(2*i-1,x1,y1,x2,y2,col,i);
   end;
end;

procedure SortXar;
var
   i,j:integer;
begin
   for i:=1 to 2*n do
   for j:=1 to 2*n-1 do
      if xar[j]>xar[j+1] then SwapInt(xar[j],xar[j+1]);
end;

procedure SortSeg;
var
   i,j:integer;
begin
   for i:=1 to 2*n do
   for j:=1 to 2*n-1 do
      if seg[j].y>seg[j+1].y then SwapRec(seg[j],seg[j+1]);
end;

procedure HeapInsert(x:integer);
var
   w:integer;
begin
   inc(HeapSize);
   w:=HeapSize;
   while Heap[w shr 1]<x do
   begin
      Heap[w]:=Heap[w shr 1];
      w:=w shr 1;
   end;
   Heap[w]:=x;
end;

procedure HeapDelete;
var
   x:integer;
   w:integer=1;
begin
   x:=Heap[HeapSize];
   dec(HeapSize);
   while w shl 1<=HeapSize do
   begin
      w:=w shl 1;
      if (w<>HeapSize) and (Heap[w+1]>Heap[w]) then inc(w);
      if Heap[w]>x then Heap[w shr 1]:=Heap[w]
      else begin
         w:=w shr 1;
         break;
      end;
   end;
   Heap[w]:=x;
end;

procedure Scan(x1,x2:integer);
var
   i:integer;
   j:integer=0;
begin
   for i:=1 to 2*n do if (seg[i].x1<=x1) and (seg[i].x2>=x2) then
   begin
      inc(ans[Color[Heap[1]]],(x2-x1)*(seg[i].y-seg[j].y));
      hash[seg[i].order]:=not hash[seg[i].order];
      if hash[seg[i].order] then HeapInsert(seg[i].order)
         else while (HeapSize>0) and not hash[Heap[1]] do HeapDelete;
      j:=i;
   end;
end;

procedure Solve;
var
   i:integer;
begin
   for i:=1 to 2*n-1 do if xar[i]<xar[i+1] then
   begin
      fillchar(Heap,Sizeof(Heap),0);
      fillchar(hash,Sizeof(hash),0);
      HeapSize:=0;
      Heap[0]:=Infinity;
      Scan(xar[i],xar[i+1]);
   end;
end;

procedure Writep;
var
   i:integer;
begin
   for i:=1 to MaxCol do
      if ans[i]>0 then writeln(i,' ',ans[i]);
end;

{====main====}
begin
   assign(input,'rect.in');
   reset(input);
   assign(output,'rect.out');
   rewrite(output);

   Readp;
   SortXar;
   SortSeg;
   Solve;
   Writep;

   close(input);
   close(output);
end.

    这几天大家发现我改PJBlog改错了什么东西导致Bug的话麻烦帮忙报告一下。事实上很有可能有人发现有Bug但是不能报告，因为我很有可能把验证码系统也搞坏了。
    如果这几天大家没有发现问题的话，我把这几天我的PJBlog个性修改方法和心得写出来分享一下（越来越喜欢搞Web Design了）。

做人要厚道
转贴请注明出处
（这篇日志没什么技术含量，感觉写上这两句很别扭）

     有一个女人的男人很幸福。事实上，这是片面的。应该说，有不止一个女人的男人更幸福。但是，这样会坏了我的人品，而且被女的知道了也不好。两个耍得好的女人话很多，秘密在女人中传得很快。于是，我打算不同时和两个耍得好的女的耍朋友。后来我意识到，这样也不行。女人太无敌了，即使A与B耍得好，B与C耍得好，A和C的消息也是互通的。哪怕只有一个朋友关系也能把两群人联系在一起。我不得不改变策略，使得我的女朋友之间没有任何渠道传递信息。也就是说，在上面的A、B、C三个人中，虽然A和C没有直接的联系，但我也不能同时和A、C耍。不久后，我想知道，某两个女人是否可以通过某条“朋友链”传递信息。这就是所谓的等价关系——基本上算是判断一个无向图的连通性。就像很多个集合，每次选两个并成一个，而且我们随时想知道某两个元素经过前面的合并后是否在同一个集合内。怎么办呢？后来有一天，我发现那些小女生喜欢玩些认亲戚的游戏，什么谁是谁妈，谁是谁姐，谁是谁女儿之类的（不知道为什么这些疯女人喜欢搞这些）。我突然恍然大悟，我的问题可以用树结构来完成。亲戚的亲戚还是亲戚，但有一点总相同：所有亲戚的始祖总是一样的。始祖一样的都是一伙的。因此，把两个集合并在一起，只要让其中一个集合的根成为另一个集合中的某个元素的一个儿子就行了，这种家谱关系的改变将使前面的集合中所有的元素拥有和后面那个集合一样的鼻祖，而这将成为这些元素的“标志”。这个想法的灵感是来自女人世界的，因此女人还是有一定的作用。
    这就叫并查集，又叫不相交集。它可以合并两个集合并且查询两个元素是否在同一集合。我们有一个很有效的剪枝：递归时顺便把路上经过的祖祖辈辈全部变成根的儿子。这样的程序只用2行来解决。
function find_set(x:integer):integer;
   begin
   if x<>p[x] then p[x]:=find_set(p[x]);
   exit(p[x]);
end;
    p[x]表示元素x的父亲的位置。一开始，p[x]都等于x自己，表示自己一个人是一个集合。函数find_set(x)将返回x所在集合（一棵树）的根。
    并查集还有些其它的剪枝和一些很复杂的效率分析问题，这里不多说了。

    写到这里，《数据结构与算法分析》中的几个大块内容算是说清楚了。由于本文的叙述调整了原书各章节的顺序且至此还没有涉及书里的一些小问题，因此这里想把遗漏下的一些小东西提一下。
    有一些树结构可能要求同时满足多个要求。比如一个简单的问题：如果要求构造一个堆使得既能查找最小元素又能查找最大元素怎么办？这时，我们可以用一个特殊的方法来实现：树的单数层满足一种性质，树的双数层满足另一种性质。我们用一个叫做最小-最大堆的东西来实现前面说的问题。这个堆的双数层的数据小于它爸大于它爸的爸，单数层的数据反过来，大于它爸小于它爸的爸。用类似的方法，我们还可以设计一个二叉查找树，使得它能够支持含有2种不同类型元素的数据。在单数层按其中一种操作，在双数层按另一种操作，这样可以方便的查找同时位于两个不同类元素的指定区间内的数据。这种二叉查找树叫做2-d树。扩展2-d 树，我们可以得到k-d树。这些数据结构的具体实现方法这里不说了，书上本来也是作为一个习题介绍的。
    书里的第7章花了近50页介绍并分析各种排序算法，分析得很全。其中第11节花了10页介绍外部排序。所谓外部排序，就是说怎样快速地把一个根本无法全部读入内存的大文件进行排序。很多排序之所以可行是因为它们可以随意读写任意一个指定的数。但在大文件里，我们无法实现“第1234567890个元素和第 123个元素交换位置”，更无法实现递归之类的操作，而只能像磁带一样“过一遍”，从头到尾扫一遍，由于文件太大内存不能接受，因此必须要读一截扔一截。于是，外部排序产生了。不要以为这个限制会把排序速度拖得很慢。事实上，外部排序同样突破了O(n^2)的界限。它借助了归并排序中的“合并两个已经有序的数组”的思想，因为这个操作可以边读就边做。把文件先拆成两个文件，再把每个文件处理成一段一段的等长有序序列（一段多大取决于内存能一次处理多大），然后不断从两个文件中各取一段出来合并。可以看到，每段有序序列的长度变长了，变成了2倍长。过不了几次，这个长度将变成文件的总长。注意，我们必须要让每次合并时为下次合并做好准备（就是说合并后的结果仍然要是两个分了段的文件）。一个好的方法是将合并的结果交替存在两个不同的新文件中。
    第9章讲图论算法。讲了图的遍历（广搜和深搜）、AOV、AOE、Dijkstra、网络流、Prim、Kruskal和NP问题。在讲深搜时，我学到了两个新东西，用线性时间查找割点（去掉了的话图就不连通了的点）和强分支（有向图中的一个分支满足其中任两个点之间都可以互相到达）。后来发现黑书上也有，又觉得这个东西很不好说，因此这里不想说了。说到了黑书还想顺便补一句：黑书真的看不得——太多错误了。不是说LRJ怎么了，LRJ在真正的大问题上有他的思想和经验，但很多细节的概念他也是昏的，这不利于初学者接受知识。不信哪天我还要写一篇日志纠正黑书的错误。引用政治书上抨击“人性自私论”的经典语言：“从理论到实践都是错的”。
    第10章讲“算法设计技巧”，大概是些贪心啊，分治啊，动规啊，回溯啊，随机化啊之类的。调度问题、Huffman树、装箱问题近似算法、最近点距分治算法、最优二叉查找树、Floyd-Warshall、跳跃表、Miller-Rabin素性测试、博弈算法等都在这章中有讲，并且讲得相当好。由于这不是本书的重点内容，这里也不说了。
    第11章整章都在讲摊还分析。这是一个相当复杂的问题，是分析时间复杂度的一个有力工具。它的分析告诉我们的不是某一个操作的复杂度，而是重复执行某一个操作的平均复杂度。研究这个是很有必要的，因为我们会遇到一些“越变越慢”的退化情形和“自我保持不变”的自调整性等数据结构，单个操作并不能反映它真正的效率。

    到这里，这本书的所有东西都已经介绍完了。总的来说，这本书很值得一看（虽然有些地方翻译得很差）。它的理论性很强，证明过程完整（再复杂的分析它也证明得很清楚，满足那些刨根问底的人）；整本书自成一个体系，前后呼应；习题具有研究性，与课文互相补充。事实上，这些都是国外教材共有的特点。这算是我完整读过的第一本国外教材，今后我还会读一些。这几天在看《组合数学》（仍然是这个出版社出版的），看完后也打算写一下“对《组合数学》一书中部分内容的形象理解”。读一本国外教材，你会发现它与国内书籍的不同并会从中获益更多。

    这篇文章就写到这里了。号称是一个5000字缩写，没想到写着写着已经超过8000字了。而且，这个并不是缩写，而是一些简单的、系统的、清晰的、形象化的思想和理解。这篇文章或许对已经知道一些有关知识的人有用，但不适合一点也没有接触过数据结构与算法分析的人。如果有一个人能从中收获一件东西，我写这个的目的也就达到了。

（完）

Matrix67原创
做人要厚道 转帖请注明出处

    堆，就是一陀一陀的东西。头重脚轻不算堆，要上面小下面大才算一个堆。堆是一棵二叉树，满足下面的始终比上面的大。它和二叉查找树比较起来既有好的又有不好的：好的就是要想知道数据里的最小值时根本就不用找了，直接就是最顶上的那个了；不好的就是堆除了这个以外基本上不能做别的事了。除了最顶上的那个以外，你几乎没办法控制其余的部分。当然，插入和删除数据这种基本操作还是可以做的。插入就是把数据暂时先放在最下面的某个位置，然后通过与它上面一个进行比较、交换不断往上冒直到已经到了自己的位置不能再向上为止。删除反起来，通过不断交换往下沉一直沉到底。因为是往下走，所以要考虑到一个把左边的放上来还是把右边的放上来的问题。当然，为了保证堆上小下大的性质，应该把小的一边换上来。刚才说过，由于你只能“看”到最顶上的东西，不知道中间部分是什么样，我们通常只删除最小的（最上面的）那个节点。其实堆还有一个最大的好处：容易写代码。因为我们可以有意让数据把树“排得满满的”，满到它是一行一行挨着排下来的。这叫做“完全二叉树”。我们可以给完全二叉树编个号，从上到下从左到右挨着数下来。根是1，找左儿子就乘2，找右儿子就乘2加1，找它爸就 div 2。以后叫谁就是谁，很方便。这样整个树就可以用一个数组实现了。由于堆基本上只用来找最小，因此如果某个问题要求很复杂的话，最好还是用成二叉查找树；当然，如果问题只要求插入、删除和找最小三种操作，你应该毫不犹豫地选择堆，毕竟找最小时堆方便得多，写起又简单。什么时候出现这种问题呢？比如说，我的女友排起队的，我每次要选一个最纯洁的，就是受那些的影响最小的人。每当我遇见了一个新的美女，我就把她放在这个队伍里合适的位置供我以后娱乐。这时，我只关心每次插入、取最小和删最小。这个队伍就可以用一个堆来优化。因此，堆还有一个形象的名字叫优先队列。如果谁问题目要求不找最小找最大怎么办，那人肯定是个傻子，把堆变通一下，上大下小不就完了吗？

    研究堆麻烦的地方就是堆的合并。如何把两个堆合并成一个堆？这个解决了很有用，至少上面的这些操作跟着全部统一了：插入就是与一个单节点的堆合并，删除根就是把根不要了，把根的左右两边（显然还是堆）合并起来。一个简单的办法就是递归地不断把根大的堆往根小的堆的右边合并，把新得到的堆替换原来的右儿子。注意递归过程中哪个根大哪个根小是不停在改变的。这样下来的结果就是典型的“右倾错误”，而且破坏了完全二叉树的完美。为此，我们想要随时保证堆的最右边尽量少。于是，干脆不要完全二叉树了，不过是多写几行代码嘛。这个不存在像二叉查找树那样“某一边越做越多”的退化问题，因为对于一个堆来说，反正我只管最顶上的东西，下面平不平衡无所谓，只要不挡我合并的道就行。于是，我们想到人为下一个能让堆尽量往左边斜的规定。这个规定就是，对于左右两个儿子来说，左边那个离它下面最近的两个儿子不全（有可能一个都没有）的节点的距离比右边那个的远。这规定看着麻烦，其实还真有效，最右边的路径的长比想像中的变得短得多。这就叫左式堆（左偏树）。这下合并倒是方便了，但合并着合并着要不了多少次右边又多了。解决的办法就是想办法随时保持左式堆的性质。办法很简单，你合并不是递归的吗？每次递归一层后再看看左右两边儿子离它下面没有两个儿子的节点哪个远，如果右边变远了就把左边右边调一下。由于我们已经没有用数组实现这玩意了，因此链表搞起很简单。这个对调左右的方法给了我们一个启发：哪里还要管什么到没有两个儿子的节点的距离嘛，既然我每次都在往右合并，我为什么不每次合并之后都把它对调到左边去呢？这种想法是可行的，事实上它还有一个另外的名字，叫斜堆。

    二项堆更强，它也是堆，也能合并，不过它已经超越了堆的境界了：它不是一个堆，而是满屋子的堆。也就是说，找最小值不能再一下子找到了，而是要把二项堆中的每个堆的顶部都看一下。二项堆的合并也很强，直接把根大的堆放在根小的堆的下面。这意味着二项堆的每个堆都可能不是二叉树了。这增加了编程的难度，不过可以用一个叫做“左儿子右兄弟”的技巧来解决问题。这个技巧，说穿了就是仍然用二叉树来表示多叉树：把树画好，然后规定节点的左儿子是下一层的最左边那个，右儿子就是它右边那个。就是说，左儿子才是真正的儿子，右儿子不过是一起生出来的。为了让二项堆好看些，让堆的个数和大小保持在一个能快速操作的数目和比例内，二项堆作出了一个明智的规定：每个堆的大小（总的节点个数）只能是1、2、4、8、16…中的一个，且每种大小的堆只能有一个。若干个互不相同的2的幂足以表示任意一个正整数，因此这个规定可以保证不管多大的二项堆都能表示出来。保持这个性质很简单，遇到两个大小相等的堆就合并起来成为一个大一号的堆。由于总是两个大小相等的堆在合并，因此二项堆中的每一个堆都有一个奇妙的样子，看看本文结束后下面附的一个大小为16的堆的示意图，再看一下，再看一下，你就能体会到了。图下面有一个用“左儿子右兄弟”法表示的同样的树，其中，往下走的线是左儿子，往右走的线是右儿子。

    最后简单说一下Fibonacci堆。保持一个跟着变的数组记录现在某个节点在堆中的位置，我们还是可以对堆里的数据进行一些操作的，至少像删除、改变数值等操作是完全可以的。但这个也需要耗费一些时间。Fibonacci堆相当开放，比二项堆更开放，它可以不花任何时间减少（只能是减少）某个节点的值。它是这样想的：你二项堆都可以养一屋子的堆，我为什么不行呢？于是，它懒得把减小了的节点一点一点地浮上去，而是直接就把它作为根拿出来当成一个新的堆。每次我要查最小值时我就再像二项堆一样（但不要求堆的大小了）一个个合并起来还原成一个堆。当然，这样的做法是有适用范围的，就是前面说的数值只能是减少。在什么时候需要一个数值只减少不增加的堆结构呢？莫过于Dijkstra一类的图论算法了。所以说，这些图论算法用Fibonacci堆优化可以进一步提速。



Matrix67原创
做人要厚道 转帖请注明出处

    4月7日买起来看，前几天才看完。这可以说明很多问题，比如，学习很紧张，没有时间；书本身很好，很有看头；看书看得很细心，很有耐心。
    打算大致写一下书里的内容。
    Data Structures and Algorithm Analysis in C, Second Edition，机械工业出版社。封面很丑，一个黑底版，上面有些大理石花纹，正中间生硬的摆一个原版封面，同样丑。一共12章，近400页。
    400多页是很多的。我们必须要“把厚书读薄”，厚的变薄的，薄的变一页，一页变一行，一行变成一个字。因此，我要在有限的字数内把整本书说完。

    算法分析，就是复杂度的问题。复杂度只算“最要命的”，比如，执行n^2的算法前来个快排根本不拖速度，n^2多的都豁出去了不在乎区区一个nlogn。书里对复杂度进行了严格的定义，包括O()、o()、Θ()、Ω()四种符号。简单地说，O(n^2)就是顶破天了搞个n^2次；o(n^2)就是天花板不到n^2，比n^2矮一点（比如希尔排序就是o(n^2)，因为它再倒霉也达不到n^2）；Ω(n^2)就是说某个算法随便怎么至少都要耗费n^2，比如所有基于比较的排序都是Ω(nlogn)；Θ(n^2)就是说它即是O(n^2)又是Ω(n^2)，被天花板和水泥地夹在中间了，动不了了，就是它了。这里面有一个经典的例子，就是最大子序列（找数列中连续一段数之和最大）的四种算法，复杂度分别为O(n^3)、O(n^2)、O(nlogn)和O (n)。这书一个特色在于，对每种数据结构都有严格的算法复杂度证明，这往往是看上去最头痛的部分。

    表、栈和队列是三个基本的数据结构。说穿了表就是把数据找起来排排坐吃果果，找什么东西都来把整个队伍找一遍。栈就是一个桶，后放进去的先拿出来，它下面本来有的东西要等它出来之后才能出来，就好像你看到了一个丑人不可能今天的中饭还没吐出来就先把早饭吐出来了。栈是拿来模拟多个过程的调用的（比如递归），实际点的用途就是表达式计算。队列好比堵车，先进去的先出来。先进队先买票，不能插队。常拿来实现广搜。

    树，是一种植物，有很多枝枝丫丫。不同的是这里的树是倒着的，树枝朝下长。最上面叫根，尖尖的地方叫树叶，生出树叶的是他爸，他爸生的是他儿子。不管是根是树叶还是儿子还是儿子他爸都叫节点。我们常常把数据储存在节点上，并且以后还要不断地插入、改变和删除数据。
    二叉树就是每个分叉的地方最多分两个岔，而且还分得清左右。二叉查找树就是说把数据存在节点上，而且左边的都比他爸小，右边的都比他爸大，以后要找哪个数就可以只找其中的一边，一半一半地扔掉。在二叉查找树里也可以插入一个数，删掉一个数（只有一个儿子好办，有两个就把右边的最小的一个拿来替代这个），找最小的数（一直往左走），找最大的数（一直往右走），但是容易搞着搞着的树就变畸形了，比如说左边猛起长右边萎缩导致以后往左边走要走很久。我们就需要一种方法来让树左右差不多一样多而且左边的值仍然比右边的小。事实上这种方法已经找到了，而且不只一种方法，而是一卡车的方法，比如AVL、Splay、红黑树、Treap等。几种方法都靠一个叫“旋转”的技巧，就是把几个节点怎么个一转，左边的就跑到右边去了一点。看下面这个图你就明白了。

         ①                   ②
        /  \      旋转       /  \
      ②   ZZ    ------>    XX  ①
     /  \                      /  \
    XX  YY                    YY  ZZ

这样一来左边就少了，如果左边的XX本来很多的话就可以往上提一层从而平衡。同样地，右边多了反过来做就是了。这只是最简单的“单旋转”，事实上还有很多其它的较复杂的旋转方法。Splay树就是把刚才访问过的节点转啊转啊转啊转转到最顶上去，Treap就是每个节点附加一个随机的数，随时通过旋转保持儿子的这些随机数比他爸大，其余的有点复杂。这些方法都能使二叉查找树相对地平衡一些，防止畸变导致的时间浪费。
    B-树和二叉查找树有两个不同，一个是节点不存数据，数据全在树叶子上，二个是它不一定是二叉。数据仍然左边小右边大方便查找。每个节点最多的儿子数有限制，最多三叉的叫2-3树，最多四叉的叫2-3-4树。因为只有树叶上有数据，所以可以递归地用分裂的方法处理新插入后出现的分叉比规定的最多的儿子个数时还多的情况。比如，2-3树中如果哪里分了四个岔，就把它重新分成两个两个的岔。我们还规定，除了根以外，每个节点最少的儿子数是规定的最多儿子数的一半，除不尽取上整。容易想到，删除的话可以把插入时的分裂反过来做，什么时候只剩一个儿子了就和旁边的合并起来。

    Hash表又叫散列表，一般用于判断有没有重复。比如我想找我们班有没有两个一天生的，我们不必每两个人都来比较一次，而是准备一个年历，让人一个一个上去在他的生日那天那里画一个圈，如果谁要画圈时发现那里已经有一个圈了，就找到了一对。这个很简单，不说了。
    那天班上流行一个心里测试，当时我还真发现了一个和我一天生的，女的。

Matrix67原创
做人要厚道 转帖请注明出处