我正在餐桌前吃早餐。餐桌上有一张圆形的大饼，有一个方形的蛋糕，还有一个甜甜圈。我依次思考了下面三个问题。你能帮我想出它们的答案吗？
- 3 刀切一张圆形的大饼，最多能把它分成多少块？或者说，3 条直线最多能把一个圆盘分成多少个区域？
- 4 刀切一个方形的蛋糕，最多能把它分成多少块？或者说，4 个平面最多能把一个正方体分成多少个区域？
- 3 刀切一个甜甜圈，最多能把它分成多少块？或者说，3 个平面最多能把一个（实心的）环面分成多少个区域？
提示：上一个问题的答案总会为下一个问题提供线索。
数列
捡石子游戏、 Wythoff 数表和一切的 Fibonacci 数列
让我们来玩一个游戏。把某个国际象棋棋子放在棋盘上，两人遵循棋子的走法，轮流移动棋子，但只能将棋子往左方、下方或者左下方移动。谁先将棋子移动到棋盘的最左下角，谁就获胜。如果把棋子放在如图所示的位置，那么你愿意先走还是后走？显然，答案与我们放的是什么棋子有关。
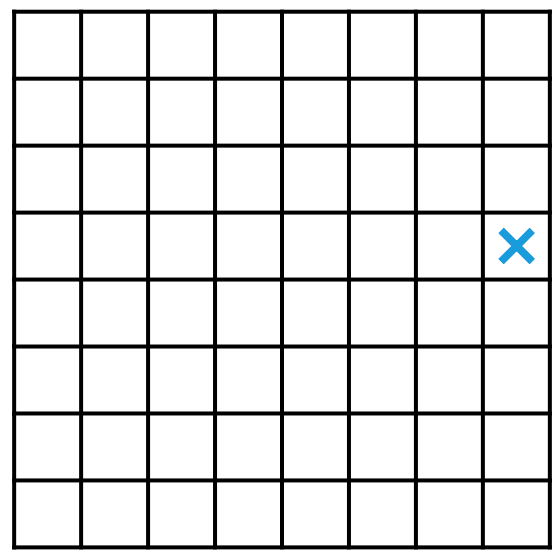
这个游戏对于兵来说是没有意义的。在如图所示的地方放马或者放象，不管怎样都无法把它移动到棋盘的最左下角，所以我们也就不分析了。因此，我们只需要研究王、后、车三种情况。
利用重心推导平方和公式
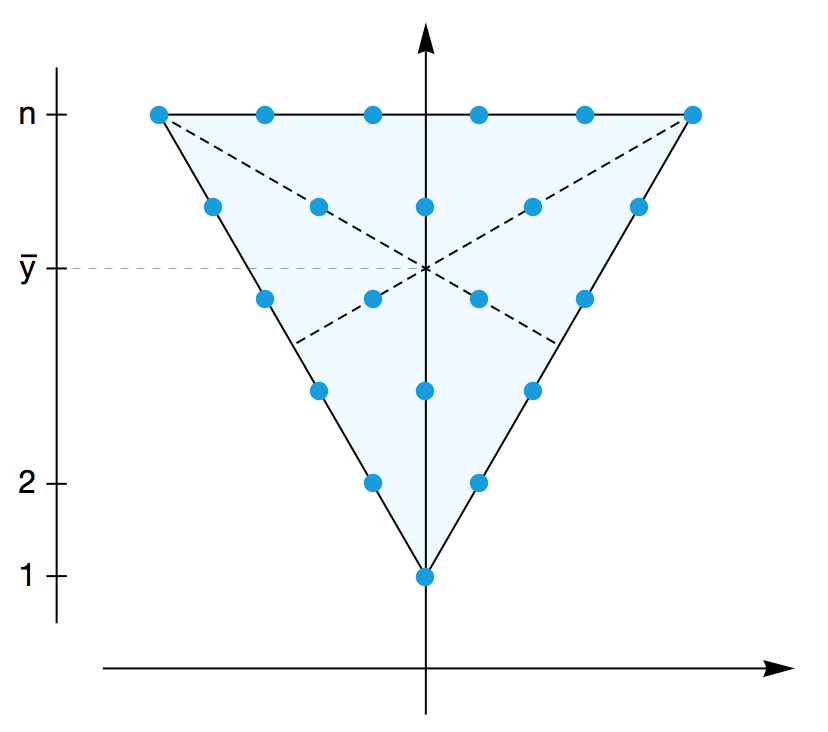
假设平面上有 1 + 2 + 3 + … + n 个小球，每个小球的质量都是 1kg 。它们排成了一个三角形阵，具体地说，它们排成了一个倒置的、以 (0, 1) 为顶点的等边三角形。这个三角形阵作为一整个物体，它的重心的 y 坐标是多少？我们有两种不同的求解方法。
寻找相邻两项之比不趋于 1.618 的广义 Fibonacci 数列
大家或许知道 Fibonacci 数列 1, 1, 2, 3, 5, 8, … 有一个非常漂亮的性质：数列中的相邻两项之比将会越来越接近黄金比例 (1 + √5) / 2 ≈ 1.618 。事实上，如果我们用 F(n) 来表示第 n 个 Fibonacci 数的话，那么当 n → ∞ 时，我们有 F(n + 1) / F(n) → (1 + √5) / 2 。
不过，可能有人并不知道，如果把 Fibonacci 数列的前两项换成两个其他的正整数（但保持 Fibonacci 数列的递推关系不变），由此所得的广义 Fibonacci 数列当中，相邻两项之比仍然会趋近于 (1 + √5) / 2 。比方说，如果数列的前两项为 7, 2 ，那么整个数列的前 15 项以及相邻两项之比的情况如下：
7, 2, 9, 11, 20, 31, 51, 82, 133, 215, 348, 563, 911, 1474, 2385, …
2 / 7 = 0.28571429…
9 / 2 = 4.5
11 / 9 = 1.2222222…
20 / 11 = 1.8181818…
31 / 20 = 1.55
51 / 31 = 1.6451613…
82 / 51 = 1.6078431…
133 / 82 = 1.6219512…
215 / 133 = 1.6165414…
348 / 215 = 1.6186047…
563 / 348 = 1.6178161…
911 / 563 = 1.6181172…
1474 / 911 = 1.6180022…
2385 / 1474 = 1.6180461…
更神奇的是，即使最前面这两个数当中有一个负数或者都是负数，相邻两项之比的趋势依旧不变！举个例子，若数列的开头两项是 20 和 -13 ，则有：
20, -13, 7, -6, 1, -5, -4, -9, -13, -22, -35, -57, -92, -149, -241, …
(-13) / 20 = -0.65
7 / (-13) = -0.53846154
(-6) / 7 = -0.85714286
1 / (-6) = -0.16666667
(-5) / 1 = -5
(-4) / (-5) = 0.8
(-9) / (-4) = 2.25
(-13) / (-9) = 1.4444444
(-22) / (-13) = 1.6923077
(-35) / (-22) = 1.5909091
(-57) / (-35) = 1.6285714
(-92) / (-57) = 1.6140351
(-149) / (-92) = 1.6195652
(-241) / (-149) = 1.6174497
事实上，不管数列的开头两项是多么奇怪的两个实数（比如 -7/2, √2, … 或者 π/10, -√e, … 等等），按照 Fibonacci 式的递推关系算出后面各项，相邻两项之比几乎总会趋于 (1 + √5) / 2 ！注意，刚才我们使用了“几乎”一词，因为这个结论其实并不总是成立。今天的题目就是：请你找出至少一个反例。也就是说，你需要找出至少一个由递推关系 a(i) = a(i – 1) + a(i – 2) 生成的数列，使得当 n 趋于无穷大时 a(n + 1) / a(n) 并不趋于 (1 + √5) / 2 。
对了， 0, 0, 0, 0, 0, … 这种情况自然不算。
杨辉三角中的自然底数 e
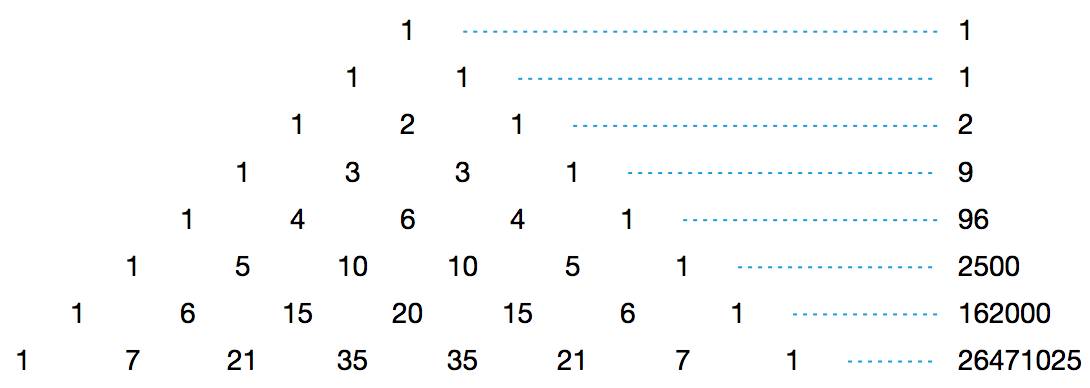
你相信吗，杨辉三角里竟然也有自然底数 e 的身影。 2012 年， Harlan Brothers 发现了杨辉三角中的一个有趣的事实。不妨把杨辉三角第 n 行的所有数之积记作 sn ，那么随着 n 的增加， sn · sn+2 / sn+12 会越来越接近 e ≈ 2.718 。事实上，我们有：
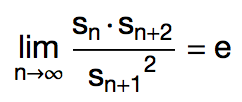
这是为什么呢？ John Baez 在这个网页上给出了一个漂亮的解释。