小时候曾想，为什么一个人从屏幕左边跑出去，立即就从屏幕右端钻进来……
现在我们知道了，因为游戏是在一个柱面上进行的……

我有预感此日志又要火了

Read more…

    有时候，一个看似更加复杂的问题反而有一个更简单的解答。
    四色问题是说，对一个平面地图进行染色，要想用不同的颜色来区别相邻的区域，最少需要多少种颜色。在很长一段时间里，人们猜想，只要四种颜色就足够了；但这个“四色猜想”却怎么也证不出来。直到上世纪70年代，“四色猜想”才在计算机的帮助下获得证明。在《从一到无穷大》一书中，作者提到了这样一个有趣的事实：平面上的四色问题一直是一个相当复杂的难题，然而有意思的是，在环面上的染色问题却只需要短短十几行文字就能得出一个完美的结论。下面我们来说明，给一个游泳圈上任意划分出来的区域进行染色，为了使相邻区域不同色，只需要7种颜色就够了。
    为了证明这一点，我们只需要说明，在一个环面图中总能找到一块区域，它的邻域不超过6块。如果真是这样的话，余下的部分用数学归纳法就直接证到了：对于一个有n个区域的图，我们找出它的一个邻域数量不超过6的区域，然后把这块区域缩小为一个点，使整个图的区域个数减少到n-1。按照我们的数学归纳，这个有n-1个区域的图是可以7染色的；并且显然地，把第n个区域添加回去后所产生的图仍然可以7染色，因为我的邻域不超过6个，我总能找一个和这些邻域都不一样的颜色。
    现在的问题就是，为什么总存在邻域数量不超过6的区域呢？注意到在环面上，有V+F-E=0，其中V表示顶点数，F表示区域数，E表示边的总条数。注意到每个顶点都发射出了至少三条边，即所有顶点引出的边数至少为3V；但每条边都被重复计算了一次（因为一条边有两个端点），因此3V/2≤E，即3V≤2E。代入V+F-E=0，得到E≤3F。假设每个区域都有7个或7个以上的邻域，那么它们将产生至少7F条边；但每条边都被重复计算了一次（因为每条边都为两块区域共享），因此7F/2≤E，即7F≤2E。于是，2E≥7F>6F≥2E，矛盾。

Read more…

    去年的一篇日志里曾经向大家提到了Smale球面外翻问题：在允许与自身相交的情况下，是否有可能无损地、平滑地、不留折痕地把一个球面的内侧翻到外面来。那篇日志里有一个视频，演示了球面外翻的其中一种解法，但没有再进行任何说明和解释。我曾在Google Video上找到了一段完整的视频，可惜Google Video不对中国大陆开放。当时我非常想看一看这段21分钟的视频，但尝试了各种方法都不行，其它地方也没有找到。今天听说中国大陆可以看Google Video的视频了，首先想到的就是去看这段视频。确实太精彩了！！你可以看到球面外翻问题有解的可能性，以及低维情形下（圆的外翻）为何反而无解。后面多个角度多种方式的动画演示足以让你完全理解这个外翻过程中的每个细节。从第11分钟开始的那个add waves则是整个视频的精华所在，太牛B了！

把地址给出来吧，如果上面这个看不了可以进这里面去看：
http://video.google.com/videoplay?docid=-6626464599825291409

    Smale球面外翻问题(Smale's Sphere Eversion Paradox)是微分拓扑学中的一个非常有趣的问题：在允许与自身相交的情况下，是否有可能无损地、平滑地、不留折痕地把一个球面的内侧翻到外面来。答案是肯定的，并且球面外翻的方法不只一种。上面这段有趣的动画里就演示了球面外翻问题的一种常见解法。你能看出这是怎么变的吗？你能把整个变换过程的每个细节都想清楚吗？你是否能在头脑里清晰地想象出整个过程？你又如何给别人解释这一过程？
    这个小程序可以帮助你观察这个球面外翻过程。你可以拉进拉远，从任意角度观察任一时刻该球面的形状。程序提供了球面透明、只查看半球等实用功能便于你一步一步进行分析。

YouTube链接：http://www.youtube.com/watch?v=R_w4HYXuo9M
了解更多：http://torus.math.uiuc.edu/jms/Papers/isama/color/opt2.htm

    虽然有些东西似乎是显然的，但一个完整的定义仍然很有必要。比如，大多数人并不知道函数的连续性是怎么定义的，虽然大家一直在用。有人可能会说，函数是不是连续的一看就知道了嘛，需要定义么。事实上，如果没有严格的定义，你很难把下面两个问题说清楚。
    你知道吗，除了常函数之外还存在其它没有最小正周期的周期函数。考虑一个这样的函数：它的定义域为全体实数，当x为有理数时f(x)=1，当x为无理数时f(x)=0。显然，任何有理数都是这个函数的一个最小正周期，因为一个有理数加有理数还是有理数，而一个无理数加有理数仍然是无理数。因此，该函数的最小正周期可以任意小。如果非要画出它的图象，大致看上去就是两根直线。请问这个函数是连续函数吗？如果把这个函数改一下，当x为无理数时f(x)=0，当x为有理数时f(x)=x，那新的函数是连续函数吗？
    Cauchy定义专门用来解决这一类问题，它严格地定义了函数的连续性。Cauchy定义是说，函数f在x=c处连续当且仅当对于一个任意小的正数ε，你总能找到一个正数δ使得对于定义域上的所有满足c-δ< x <c+δ的x都有f(c)-ε<f(x)<f(c)+ε。直观地说，如果函数上有一点P，对于任意小的ε，P点左右一定范围内的点与P的纵坐标之差均小于ε，那么函数在P点处连续。这样就保证了P点两旁的点与P无限接近，也就是我们常说的“连续”。这又被称作为Epsilon-Delta定义，可以写成“ε-δ定义”。
    有了Cauchy定义，回过头来看前面的问题，我们可以推出：第一个函数在任何一点都不连续，因为当ε< 1时，δ范围内总存在至少一个点跳出了ε的范围；第二个函数只在x=0处是连续的，因为此时不管ε是多少，只需要δ比ε小一点就可以满足ε-δ定义了。
    在拓扑学中，也有类似于ε-δ的连续性定义。假如一个函数f(t)对应空间中的点，对于任意小的正数ε，总能找到一个δ使得定义域(t-δ,t+δ)对应的所有点与f(t)的距离都不超过ε，那么我们就说f(t)所对应的曲线在点f(t)处连续。

    回到我们的话题，如何构造一条曲线使得它可以填满整个平面。在这里我们仅仅说明存在一条填满单位正方形的曲线就够了，因为将此单位正方形平铺在平面上就可以得到填满整个平面的曲线。大多数人可能会想到下面这种构造方法：先画一条单位长的曲线，然后把它变成一个几字形，接着把每一条水平的小横线段变成一个几字形，然后不断迭代下去，最后得到的图形一定可以填满整个单位正方形。我们甚至可以递归地定义出一个描述此图形的函数：将定义域平均分成五份，第二和第四份对应两条竖直线段上的点，并继续对剩下的三个区间重复进行这种操作。这个函数虽然分布得有些“不均匀”，但它确实是一个合法的函数。最后的图形显然可以填充一个正方形，但它是不是一条曲线我们还不知道呢。稍作分析你会发现这条“曲线”根本不符合前面所说的ε-δ定义，考虑任何一个可以无限细分的地方（比如x=1/2处），只要ε<1/2，δ再小其范围内也有一条竖线捅破ε的界线。这就好像当n趋于无穷时sin(nx)根本不是一条确定的曲线一样，因为某个特定的函数值根本不能汇聚到一点。考虑到这一点，我们能想到的很多可以填满平面的“曲线”都不是真正意义上的连续曲线。为了避免这样的情况出现，这条曲线必须“先把自己周围填满再延伸出去”，而填满自己周围前又必须先填满“更小规模的周围”。这让我们联想到分形图形。

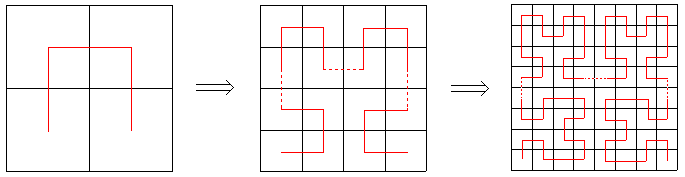
    德国数学家David Hilbert发现了这样一种可以填满整个单位正方形的分形曲线，他称它为Hilbert曲线。我们来看一看这条曲线是怎么构造出来的。首先，我们把一个正方形分割为4个小正方形，然后从左下角的那个小正方形开始，画一条线经过所有小正方形，最后到达右下角。现在，我们把这个正方形分成16个小正方形，目标同样是从左下角出发遍历所有的格子最后到达右下角。而在这之前我们已经得到了一个2×2方格的遍历方法，我们正好可以用它。把两个2×2的格子原封不动地放在上面两排，右旋90度放在左下，左旋90度放在右下，然后再补三条线段把它们连起来。现在我们得到了一种从左下到右下遍历4×4方格的方法，而这又可以用于更大规模的图形中。用刚才的方法把四个4×4的方格放到8×8的方格中，我们就得到了一条经过所有64个小方格的曲线。不断地这样做下去，无限多次地迭代后，每个方格都变得无穷小，最后的图形显然经过了方格上所有的点，它就是我们所说的Hilbert曲线。下图是一个迭代了n多次后的图形，大致上反映出Hilbert曲线的样子。
        

    根据上面这种方法，我们可以构造出函数f(t)使它能映射到单位正方形中的所有点。Hilbert曲线首先经过单位正方形左下1/4的所有点，然后顺势北上，东征到右上角，最后到达东南方的1/4正方形，其中的每一个阶段都是一个边长缩小了一半的“小Hilbert曲线”。函数f(t)也如此定义：[0,1/4]对应左下角的小正方形中所有的点，[1/4,1/2]就对应左上角，依此类推。每个区间继续划分为四份，依次对应面积为1/16的正方形，并无限制地这么细分下去。注意这里的定义域划分都是闭区间的形式，这并不会发生冲突，因为所有m/4^n处的点都是两个小Hilbert曲线的“交接处”。比如那个f(1/4)点就是左上左下两块1/4正方形共有的，即单位正方形正左边的那一点。这个函数是一条根正苗红的连续曲线，完全符合ε-δ定义，因为f(t-δ)和f(t+δ)显然都在f(t)的周围。
    Hilbert曲线是一条经典的分形曲线。它违背了很多常理。比如，把Hilbert曲线平铺在整个平面上，它就成了一条填满整个平面的曲线。两条Hilbert曲线对接可以形成一个封闭曲线，而这个封闭曲线竟然没有内部空间。回想我们上次介绍的Hausdorff维度，你会发现这条曲线是二维的，因为它包含自身4份，每一份的一维大小都是原来的一半，因此维度等于log(4)/log(2)。这再一次说明了它可以填满整个平面。

    Hilbert曲线的价值在于建立一维空间与二维空间一一对应的关系。Hilbert曲线可以看作是一个一维空间到二维空间的映射，也就是说我们证明了直线上的点和平面上的点一样多（集合的势相同）。Hilbert曲线也是一种遍历二维格点的方法，它同样可以用来证明自然数和有理数一样多。如果你已经知道此结论的Cantor证明，你会立刻明白Hilbert遍历法的证明，这里就不再多说了。当然，Hilbert曲线也可以扩展到三维空间，甚至更高维的空间，从而建立一维到任意多维的映射关系。下图就是一个三维Hilbert曲线（在迭代